D1.03: Examples 6–9
Example 6
Find the area of this trapezoid, where the numbers represent feet.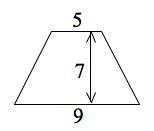
Answer: The formula is [latex]A=\frac{1}{2}h\left({{b}_{1}}+{{b}_{2}}\right)[/latex]where h is the height, [latex]{{b}_{1}}[/latex] and [latex]{{b}_{2}}[/latex] are the lengths of the two bases, and A is the area. Notice that the subscripts are used because both these sides are called bases, so b is a reasonable letter to use, but there are two different ones. We use subscripts on the b’s to distinguish between the two different bases.
Example 7
Find the volume of a sphere with radius 3 inches. The formula is [latex]V=\frac{4}{3}\pi{{r}^{3}}[/latex].Answer: [latex]V=\frac{4}{3}\pi{{r}^{3}}=\frac{4}{3}\pi{{\left(3\right)}^{3}}=\frac{4}{3}\pi\cdot27=113.097[/latex]. So the volume of this sphere is 113.097 cubic inches.
Example 8
Graph the formula [latex]V=\frac{4}{3}\pi{{r}^{3}}[/latex] for the values of r from 0 to 6 feet and use the graph to approximate what radius will give a volume of 400 cubic feet.Answer: Notice that r is the input value and V is the output value.
| r | V |
|---|---|
| 0 | 0 |
| 1 | 4.188787 |
| 2 | 33.51029 |
| 3 | 113.0972 |
| 4 | 268.0823 |
| 5 | 523.5983 |
| 6 | 904.7779 |
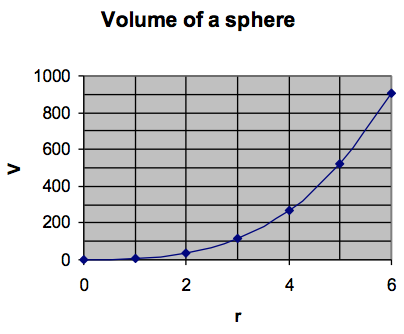 Using the graph, we follow the line for 400 on the vertical axis across to the graph and then down to see the corresponding r value, which is approximately [latex]r=4.5[/latex] feet. We can check this by plugging in and finding that [latex]V=\frac{4}{3}\pi{{(4.5)}^{3}}=381.7[/latex]
If we wanted to get a better estimate, we would try a somewhat higher value for r.
Using the graph, we follow the line for 400 on the vertical axis across to the graph and then down to see the corresponding r value, which is approximately [latex]r=4.5[/latex] feet. We can check this by plugging in and finding that [latex]V=\frac{4}{3}\pi{{(4.5)}^{3}}=381.7[/latex]
If we wanted to get a better estimate, we would try a somewhat higher value for r.
Example 9
Consider the problem of Example 8. Use graphical and numerical methods to find a value for the radius that will give a volume of 400 cubic feet, correct to within 10 cubic feet.Answer: The graph tells us that a good estimate for the radius is 4.5 feet. Next we check that by plugging in and finding that [latex]V=\frac{4}{3}\pi{{(4.5)}^{3}}=381.7[/latex]cubic feet. That’s a bit too low, so let’s try a slightly larger value for the radius. Let’s try 4.6 feet. [latex]V=\frac{4}{3}\pi{{(4.6)}^{3}}=407.72[/latex] cubic feet. That’s an adequate answer, according to the tolerance level stated in the problem. Of course, if we wanted a more accurate answer, we could continue to work numerically by taking a value for the radius just a bit smaller than 4.6 feet and finding the volume for that.
Licenses & Attributions
CC licensed content, Shared previously
- Mathematics for Measuring. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution.
