Numeration
Historical Counting Systems Introduction and Basic Number and Counting Systems
Introduction
As we begin our journey through the history of mathematics, one question to be asked is “Where do we start?” Depending on how you view mathematics or numbers, you could choose any of a number of launching points from which to begin. Howard Eves suggests the following list of possibilities.[footnote]Eves, Howard; An Introduction to the History of Mathematics, p. 9.[/footnote] Where to start the study of the history of mathematics…- At the first logical geometric “proofs” traditionally credited to Thales of Miletus (600 BCE).
- With the formulation of methods of measurement made by the Egyptians and Mesopotamians/Babylonians.
- Where prehistoric peoples made efforts to organize the concepts of size, shape, and number.
- In pre-human times in the very simple number sense and pattern recognition that can be displayed by certain animals, birds, etc.
- Even before that in the amazing relationships of numbers and shapes found in plants.
- With the spiral nebulae, the natural course of planets, and other universe phenomena.
Recognition of More vs. Less
The idea of number and the process of counting goes back far beyond history began to be recorded. There is some archeological evidence that suggests that humans were counting as far back as 50,000 years ago.[footnote]Eves, p. 9.[/footnote] However, we do not really know how this process started or developed over time. The best we can do is to make a good guess as to how things progressed. It is probably not hard to believe that even the earliest humans had some sense of more and less. Even some small animals have been shown to have such a sense. For example, one naturalist tells of how he would secretly remove one egg each day from a plover’s nest. The mother was diligent in laying an extra egg every day to make up for the missing egg. Some research has shown that hens can be trained to distinguish between even and odd numbers of pieces of food.[footnote]McLeish, John; The Story of Numbers—How Mathematics Has Shaped Civilization, p. 7.[/footnote] With these sorts of findings in mind, it is not hard to conceive that early humans had (at least) a similar sense of more and less. However, our conjectures about how and when these ideas emerged among humans are simply that; educated guesses based on our own assumptions of what might or could have been.The Need for Simple Counting
As societies and humankind evolved, simply having a sense of more or less, even or odd, etc., would prove to be insufficient to meet the needs of everyday living. As tribes and groups formed, it became important to be able to know how many members were in the group, and perhaps how many were in the enemy’s camp. Certainly it was important for them to know if the flock of sheep or other possessed animals were increasing or decreasing in size. “Just how many of them do we have, anyway?” is a question that we do not have a hard time imagining them asking themselves (or each other). In order to count items such as animals, it is often conjectured that one of the earliest methods of doing so would be with “tally sticks.” These are objects used to track the numbers of items to be counted. With this method, each “stick” (or pebble, or whatever counting device being used) represents one animal or object. This method uses the idea of one to one correspondence. In a one to one correspondence, items that are being counted are uniquely linked with some counting tool. Figure 1.
Figure 1. Figure 2.
Figure 2.Spoken Words
As methods for counting developed, and as language progressed as well, it is natural to expect that spoken words for numbers would appear. Unfortunately, the developments of these words, especially those corresponding to the numbers from one through ten, are not easy to trace. Past ten, however, we do see some patterns:- Eleven comes from “ein lifon,” meaning “one left over.”
- Twelve comes from “twe lif,” meaning “two left over.”
- Thirteen comes from “Three and ten” as do fourteen through nineteen.
- Twenty appears to come from “twe-tig” which means “two tens.”
- Hundred probably comes from a term meaning “ten times.”
Written Numbers
When we speak of “written” numbers, we have to be careful because this could mean a variety of things. It is important to keep in mind that modern paper is only a little more than 100 years old, so “writing” in times past often took on forms that might look quite unfamiliar to us today. As we saw earlier, some might consider wooden sticks with notches carved in them as writing as these are means of recording information on a medium that can be “read” by others. Of course, the symbols used (simple notches) certainly did not leave a lot of flexibility for communicating a wide variety of ideas or information. Other mediums on which “writing” may have taken place include carvings in stone or clay tablets, rag paper made by hand (twelfth century in Europe, but earlier in China), papyrus (invented by the Egyptians and used up until the Greeks), and parchments from animal skins. And these are just a few of the many possibilities. These are just a few examples of early methods of counting and simple symbols for representing numbers. Extensive books, articles and research have been done on this topic and could provide enough information to fill this entire course if we allowed it to. The range and diversity of creative thought that has been used in the past to describe numbers and to count objects and people is staggering. Unfortunately, we don’t have time to examine them all, but it is fun and interesting to look at one system in more detail to see just how ingenious people have been.The Number and Counting System of the Inca Civilization
Background
There is generally a lack of books and research material concerning the historical foundations of the Americas. Most of the “important” information available concentrates on the eastern hemisphere, with Europe as the central focus. The reasons for this may be twofold: first, it is thought that there was a lack of specialized mathematics in the American regions; second, many of the secrets of ancient mathematics in the Americas have been closely guarded.[footnote]Diana, Lind Mae; The Peruvian Quipu in Mathematics Teacher, Issue 60 (Oct., 1967), p. 623–28.[/footnote] The Peruvian system does not seem to be an exception here. Two researchers, Leland Locke and Erland Nordenskiold, have carried out research that has attempted to discover what mathematical knowledge was known by the Incas and how they used the Peruvian quipu, a counting system using cords and knots, in their mathematics. These researchers have come to certain beliefs about the quipu that we will summarize here.Counting Boards
It should be noted that the Incas did not have a complicated system of computation. Where other peoples in the regions, such as the Mayans, were doing computations related to their rituals and calendars, the Incas seem to have been more concerned with the simpler task of record-keeping. To do this, they used what are called the “quipu” to record quantities of items. (We will describe them in more detail in a moment.) However, they first often needed to do computations whose results would be recorded on quipu. To do these computations, they would sometimes use a counting board constructed with a slab of stone. In the slab were cut rectangular and square compartments so that an octagonal (eight-sided) region was left in the middle. Two opposite corner rectangles were raised. Another two sections were mounted on the original surface of the slab so that there were actually three levels available. In the figure shown, the darkest shaded corner regions represent the highest, third level. The lighter shaded regions surrounding the corners are the second highest levels, while the clear white rectangles are the compartments cut into the stone slab.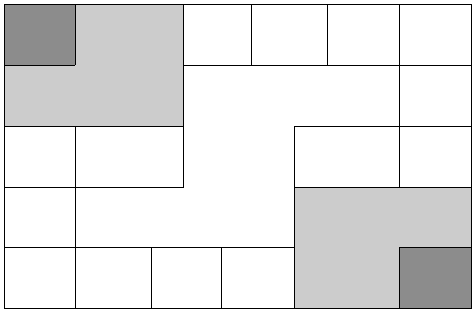 Figure 3.
Figure 3.Example 1
Suppose you have the following counting board with two different kind of pebbles places as illustrated. Let the solid black pebble represent a dog and the striped pebble represent a cat. How many dogs are being represented?Solution
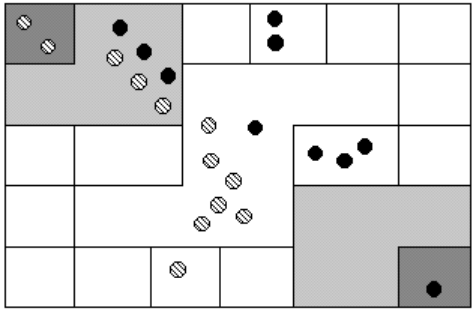 Figure 4.
Figure 4.Try It Now
How many cats are represented on this board?The Quipu
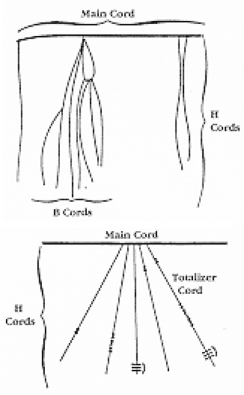 Figure 5.
Figure 5.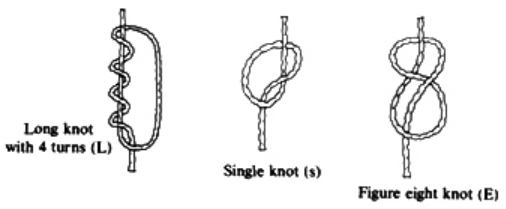 Figure 6
Figure 6Example 2
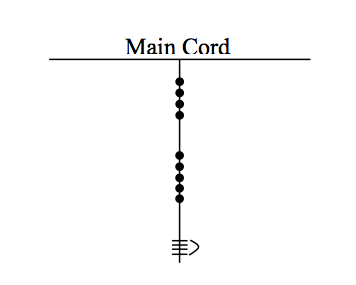 Figure 7.
Figure 7.Solution
On the cord, we see a long knot with four turns in it…this represents four in the ones place. Then 5 single knots appear in the tens position immediately above that, which represents 5 tens, or 50. Finally, 4 single knots are tied in the hundreds, representing four 4 hundreds, or 400. Thus, the total shown on this cord is 454.Try It Now
What numbers are represented on each of the four cords hanging from the main cord?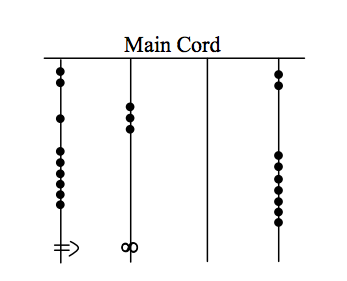 Figure 8.
Figure 8.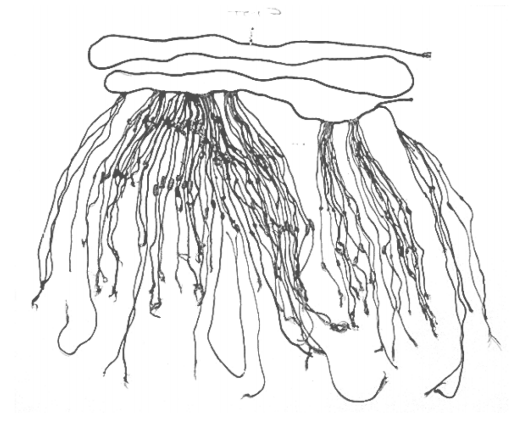 Figure 9.
Figure 9.The Hindu—Arabic Number System
The Evolution of a System
Our own number system, composed of the ten symbols {0,1,2,3,4,5,6,7,8,9} is called the Hindu-Arabic system. This is a base-ten (decimal) system since place values increase by powers of ten. Furthermore, this system is positional, which means that the position of a symbol has bearing on the value of that symbol within the number. For example, the position of the symbol 3 in the number 435,681 gives it a value much greater than the value of the symbol 8 in that same number. We’ll explore base systems more thoroughly later. The development of these ten symbols and their use in a positional system comes to us primarily from India.[footnote]http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html[/footnote] Figure 10. Al-Biruni
Figure 10. Al-Biruni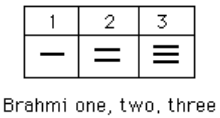 These numerals were used all the way up to the fourth century CE, with variations through time and geographic location. For example, in the first century CE, one particular set of Brahmi numerals took on the following form:[footnote]http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html[/footnote]
These numerals were used all the way up to the fourth century CE, with variations through time and geographic location. For example, in the first century CE, one particular set of Brahmi numerals took on the following form:[footnote]http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html[/footnote]
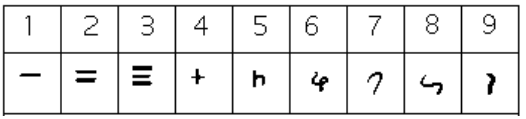 From the fourth century on, you can actually trace several different paths that the Brahmi numerals took to get to different points and incarnations. One of those paths led to our current numeral system, and went through what are called the Gupta numerals. The Gupta numerals were prominent during a time ruled by the Gupta dynasty and were spread throughout that empire as they conquered lands during the fourth through sixth centuries. They have the following form:[footnote]Ibid.[/footnote]
From the fourth century on, you can actually trace several different paths that the Brahmi numerals took to get to different points and incarnations. One of those paths led to our current numeral system, and went through what are called the Gupta numerals. The Gupta numerals were prominent during a time ruled by the Gupta dynasty and were spread throughout that empire as they conquered lands during the fourth through sixth centuries. They have the following form:[footnote]Ibid.[/footnote]
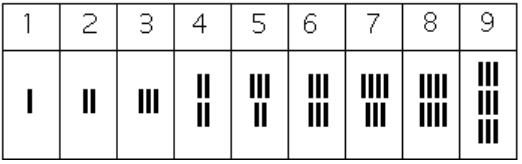
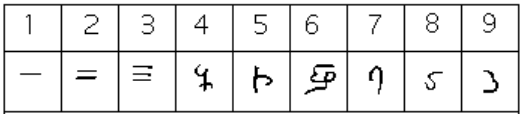 How the numbers got to their Gupta form is open to considerable debate. Many possible hypotheses have been offered, most of which boil down to two basic types.[footnote]Ibid.[/footnote] The first type of hypothesis states that the numerals came from the initial letters of the names of the numbers. This is not uncommon . . . the Greek numerals developed in this manner. The second type of hypothesis states that they were derived from some earlier number system. However, there are other hypotheses that are offered, one of which is by the researcher Ifrah. His theory is that there were originally nine numerals, each represented by a corresponding number of vertical lines. One possibility is this:[footnote]Ibid.[/footnote]
How the numbers got to their Gupta form is open to considerable debate. Many possible hypotheses have been offered, most of which boil down to two basic types.[footnote]Ibid.[/footnote] The first type of hypothesis states that the numerals came from the initial letters of the names of the numbers. This is not uncommon . . . the Greek numerals developed in this manner. The second type of hypothesis states that they were derived from some earlier number system. However, there are other hypotheses that are offered, one of which is by the researcher Ifrah. His theory is that there were originally nine numerals, each represented by a corresponding number of vertical lines. One possibility is this:[footnote]Ibid.[/footnote]
 Because these symbols would have taken a lot of time to write, they eventually evolved into cursive symbols that could be written more quickly. If we compare these to the Gupta numerals above, we can try to see how that evolutionary process might have taken place, but our imagination would be just about all we would have to depend upon since we do not know exactly how the process unfolded.
The Gupta numerals eventually evolved into another form of numerals called the Nagari numerals, and these continued to evolve until the eleventh century, at which time they looked like this:[footnote]Ibid.[/footnote]
Because these symbols would have taken a lot of time to write, they eventually evolved into cursive symbols that could be written more quickly. If we compare these to the Gupta numerals above, we can try to see how that evolutionary process might have taken place, but our imagination would be just about all we would have to depend upon since we do not know exactly how the process unfolded.
The Gupta numerals eventually evolved into another form of numerals called the Nagari numerals, and these continued to evolve until the eleventh century, at which time they looked like this:[footnote]Ibid.[/footnote]
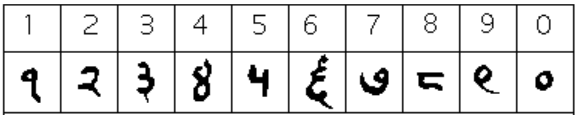 Note that by this time, the symbol for 0 has appeared! The Mayans in the Americas had a symbol for zero long before this, however, as we shall see later in the chapter.
These numerals were adopted by the Arabs, most likely in the eighth century during Islamic incursions into the northern part of India.[footnote]Katz, page 230[/footnote] It is believed that the Arabs were instrumental in spreading them to other parts of the world, including Spain (see below).
Other examples of variations up to the eleventh century include:[footnote]Burton, David M., History of Mathematics, An Introduction, p. 254–255[/footnote]
Note that by this time, the symbol for 0 has appeared! The Mayans in the Americas had a symbol for zero long before this, however, as we shall see later in the chapter.
These numerals were adopted by the Arabs, most likely in the eighth century during Islamic incursions into the northern part of India.[footnote]Katz, page 230[/footnote] It is believed that the Arabs were instrumental in spreading them to other parts of the world, including Spain (see below).
Other examples of variations up to the eleventh century include:[footnote]Burton, David M., History of Mathematics, An Introduction, p. 254–255[/footnote]
 Figure 11. Devangari, eighth century
Figure 11. Devangari, eighth century Figure 12. West Arab Gobar, tenth century
Figure 12. West Arab Gobar, tenth century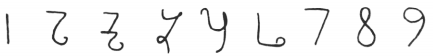 Figure 13. Spain, 976 BCE
Figure 13. Spain, 976 BCE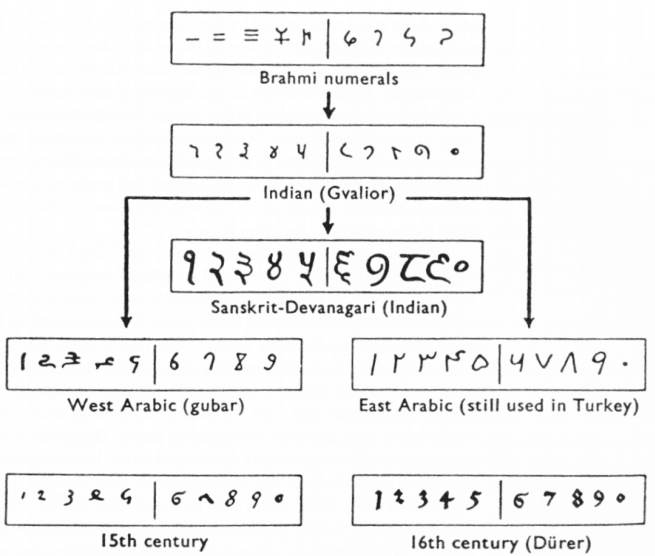 Figure 14.
Figure 14.The Positional System
More important than the form of the number symbols is the development of the place value system. Although it is in slight dispute, the earliest known document in which the Indian system displays a positional system dates back to 346 CE. However, some evidence suggests that they may have actually developed a positional system as far back as the first century CE. The Indians were not the first to use a positional system. The Babylonians (as we will see in Chapter 3) used a positional system with 60 as their base. However, there is not much evidence that the Babylonian system had much impact on later numeral systems, except with the Greeks. Also, the Chinese had a base-10 system, probably derived from the use of a counting board.[footnote]Ibid, page 230[/footnote] Some believe that the positional system used in India was derived from the Chinese system. Wherever it may have originated, it appears that around 600 CE, the Indians abandoned the use of symbols for numbers higher than nine and began to use our familiar system where the position of the symbol determines its overall value.[footnote]Ibid, page 231.[/footnote] Numerous documents from the seventh century demonstrate the use of this positional system. Interestingly, the earliest dated inscriptions using the system with a symbol for zero come from Cambodia. In 683, the 605th year of the Saka era is written with three digits and a dot in the middle. The 608th year uses three digits with a modern 0 in the middle.[footnote]Ibid, page 232.[/footnote] The dot as a symbol for zero also appears in a Chinese work (Chiu-chih li). The author of this document gives a strikingly clear description of how the Indian system works:Using the [Indian] numerals, multiplication and division are carried out. Each numeral is written in one stroke. When a number is counted to ten, it is advanced into the higher place. In each vacant place a dot is always put. Thus the numeral is always denoted in each place. Accordingly there can be no error in determining the place. With the numerals, calculations is easy.[footnote]Ibid, page 232.[/footnote]
Transmission to Europe
It is not completely known how the system got transmitted to Europe. Traders and travelers of the Mediterranean coast may have carried it there. It is found in a tenth-century Spanish manuscript and may have been introduced to Spain by the Arabs, who invaded the region in 711 CE and were there until 1492. In many societies, a division formed between those who used numbers and calculation for practical, every day business and those who used them for ritualistic purposes or for state business.[footnote]McLeish, p. 18[/footnote] The former might often use older systems while the latter were inclined to use the newer, more elite written numbers. Competition between the two groups arose and continued for quite some time. Figure 15.
Figure 15.The Development and Use of Different Number Bases
Introduction and Basics
During the previous discussions, we have been referring to positional base systems. In this section of the chapter, we will explore exactly what a base system is and what it means if a system is “positional.” We will do so by first looking at our own familiar, base-ten system and then deepen our exploration by looking at other possible base systems. In the next part of this section, we will journey back to Mayan civilization and look at their unique base system, which is based on the number 20 rather than the number 10. A base system is a structure within which we count. The easiest way to describe a base system is to think about our own base-ten system. The base-ten system, which we call the “decimal” system, requires a total of ten different symbols/digits to write any number. They are, of course, 0, 1, 2, . . . , 9. The decimal system is also an example of a positional base system, which simply means that the position of a digit gives its place value. Not all civilizations had a positional system even though they did have a base with which they worked. In our base-ten system, a number like 5,783,216 has meaning to us because we are familiar with the system and its places. As we know, there are six ones, since there is a 6 in the ones place. Likewise, there are seven “hundred thousands,” since the 7 resides in that place. Each digit has a value that is explicitly determined by its position within the number. We make a distinction between digit, which is just a symbol such as 5, and a number, which is made up of one or more digits. We can take this number and assign each of its digits a value. One way to do this is with a table, which follows:| 5,000,000 | = 5 × 1,000,000 | = 5 × 106 | Five million |
| +700,000 | = 7 × 100,000 | = 7 × 105 | Seven hundred thousand |
| +80,000 | = 8 × 10,000 | = 8 × 104 | Eighty thousand |
| +3,000 | = 3 × 1000 | = 3 × 103 | Three thousand |
| +200 | = 2 × 100 | = 2 × 102 | Two hundred |
| +10 | = 1 × 10 | = 1 × 101 | Ten |
| +6 | = 6 × 1 | = 6 × 100 | Six |
| 5,783,216 | Five million, seven hundred eighty-three thousand, two hundred sixteen | ||
Other Bases
For example, let’s suppose we adopt a base-five system. The only modern digits we would need for this system are 0,1,2,3 and 4. What are the place values in such a system? To answer that, we start with the ones place, as most base systems do. However, if we were to count in this system, we could only get to four (4) before we had to jump up to the next place. Our base is 5, after all! What is that next place that we would jump to? It would not be tens, since we are no longer in base-ten. We’re in a different numerical world. As the base-ten system progresses from 100 to 101, so the base-five system moves from 50 to 51 = 5. Thus, we move from the ones to the fives. After the fives, we would move to the 52 place, or the twenty fives. Note that in base-ten, we would have gone from the tens to the hundreds, which is, of course, 102. Let’s take an example and build a table. Consider the number 30412 in base five. We will write this as 304125, where the subscript 5 is not part of the number but indicates the base we’re using. First off, note that this is NOT the number “thirty thousand, four hundred twelve.” We must be careful not to impose the base-ten system on this number. Here’s what our table might look like. We will use it to convert this number to our more familiar base-ten system.| Base 5 | This column coverts to base-ten | In Base-Ten | |
| 3 × 54 | = 3 × 625 | = 1875 | |
| + | 0 × 53 | = 0 × 125 | = 0 |
| + | 4 × 52 | = 4 × 25 | = 100 |
| + | 1 × 51 | = 1 × 5 | = 5 |
| + | 2 × 50 | = 2 × 1 | = 2 |
| Total | 1982 |
Example 3
Convert 62347 to a base 10 number.Solution
We first note that we are given a base-7 number that we are to convert. Thus, our places will start at the ones (70), and then move up to the 7s, 49s (72), etc. Here’s the breakdown:| Base 7 | Convert | Base 10 | |
| = 6 × 73 | = 6 × 343 | = 2058 | |
| + | = 2 × 72 | = 2 × 49 | = 98 |
| + | = 3 × 7 | = 3 × 7 | = 21 |
| + | = 4 × 1 | = 4 × 1 | = 4 |
| Total | 2181 |
Try It Now
Convert 410657 to a base 10 number.Converting from Base 10 to Other Bases
Converting from an unfamiliar base to the familiar decimal system is not that difficult once you get the hang of it. It’s only a matter of identifying each place and then multiplying each digit by the appropriate power. However, going the other direction can be a little trickier. Suppose you have a base-ten number and you want to convert to base-five. Let’s start with some simple examples before we get to a more complicated one.Example 4
Convert twelve to a base-five number.Solution
We can probably easily see that we can rewrite this number as follows:12 = (2 × 5) + (2 × 1)
Hence, we have two fives and 2 ones. Hence, in base-five we would write twelve as 225. Thus, 1210 =225.Example 5
Convert sixty-nine to a base-five number.Solution
We can see now that we have more than 25, so we rewrite sixty-nine as follows:69 = (2 × 25) + (3 × 5) + (4 × 1)
Here, we have two twenty-fives, 3 fives, and 4 ones. Hence, in base five we have 234. Thus, 6910 = 2345.Example 6
Convert the base-seven number 32617 to base 10.Solution
The powers of 7 are:70 = 1 71 = 7 72 = 49 73 = 343 Etc…
32617 = (3 × 343) + (2 × 49) + (6 × 7) + (1 × 1) =117010. Thus 32617 = 117010.Try It Now
Convert 143 to base 5Try It Now
Convert the base-three number 210213 to base 10.Converting from Base 10 to Base b
- Find the highest power of the base b that will divide into the given number at least once and then divide.
- Write down the whole number part, then use the remainder from division in the next step.
- Repeat step two, dividing by the next highest power of the base b, writing down the whole number part (including 0), and using the remainder in the next step.
- Continue until the remainder is smaller than the base. This last remainder will be in the “ones” place.
- Collect all your whole number parts to get your number in base b notation.
Example 7
Convert the base-ten number 348 to base-five.Solution
The powers of five are:50 = 1 51 = 5 52 = 25 53 = 125 54 = 625 Etc…
Since 348 is smaller than 625, but bigger than 125, we see that 53 = 125 is the highest power of five present in 348. So we divide 125 into 348 to see how many of them there are:348 ÷ 125 = 2 with remainder 98
We write down the whole part, 2, and continue with the remainder. There are 98 left over, so we see how many 25s (the next smallest power of five) there are in the remainder:98 ÷ 25 = 3 with remainder 23
We write down the whole part, 2, and continue with the remainder. There are 23 left over, so we look at the next place, the 5s:23 ÷ 5 = 4 with remainder 3
This leaves us with 3, which is less than our base, so this number will be in the “ones” place. We are ready to assemble our base-five number:348 = (2 × 53) + (3 × 52) + (4 × 51) + (3 × 1)
Hence, our base-five number is 2343. We’ll say that 34810 = 23435.Example 8
Convert the base-ten number 4,509 to base-seven.Solution
The powers of 7 are:70 = 1 71 = 7 72 = 49 73 = 343 74 = 2401 75 = 16807 Etc…
The highest power of 7 that will divide into 4,509 is 74 = 2401. With division, we see that it will go in 1 time with a remainder of 2108. So we have 1 in the 74 place. The next power down is 73 = 343, which goes into 2108 six times with a new remainder of 50. So we have 6 in the 73 place. The next power down is 72 = 49, which goes into 50 once with a new remainder of 1. So there is a 1 in the 72 place. The next power down is 71 but there was only a remainder of 1, so that means there is a 0 in the 7s place and we still have 1 as a remainder. That, of course, means that we have 1 in the ones place. Putting all of this together means that 4,50910 = 161017.Try It Now
Convert 65710 to a base 4 number.Try It Now
Convert 837710 to a base 8 number.Another Method For Converting From Base 10 to Other Bases
As you read the solution to this last example and attempted the “Try it Now” problems, you may have had to repeatedly stop and think about what was going on. The fact that you are probably struggling to follow the explanation and reproduce the process yourself is mostly due to the fact that the non-decimal systems are so unfamiliar to you. In fact, the only system that you are probably comfortable with is the decimal system. As budding mathematicians, you should always be asking questions like “How could I simplify this process?” In general, that is one of the main things that mathematicians do: they look for ways to take complicated situations and make them easier or more familiar. In this section we will attempt to do that. To do so, we will start by looking at our own decimal system. What we do may seem obvious and maybe even intuitive but that’s the point. We want to find a process that we readily recognize works and makes sense to us in a familiar system and then use it to extend our results to a different, unfamiliar system. Let’s start with the decimal number, 486310. We will convert this number to base 10. Yeah, I know it’s already in base 10, but if you carefully follow what we’re doing, you’ll see it makes things work out very nicely with other bases later on. We first note that the highest power of 10 that will divide into 4863 at least once is 103 = 1000. In general, this is the first step in our new process; we find the highest power that a given base that will divide at least once into our given number. We now divide 1000 into 4863:4863 ÷ 1000 = 4.863
This says that there are four thousands in 4863 (obviously). However, it also says that there are 0.863 thousands in 4863. This fractional part is our remainder and will be converted to lower powers of our base (10). If we take that decimal and multiply by 10 (since that’s the base we’re in) we get the following:0.863 × 10 = 8.63
Why multiply by 10 at this point? We need to recognize here that 0.863 thousands is the same as 8.63 hundreds. Think about that until it sinks in.(0.863)(1000) = 863 (8.63)(100) = 863
These two statements are equivalent. So, what we are really doing here by multiplying by 10 is rephrasing or converting from one place (thousands) to the next place down (hundreds).0.863 × 10 ⇒ 8.63 (Parts of Thousands) × 10 ⇒ Hundreds
What we have now is 8 hundreds and a remainder of 0.63 hundreds, which is the same as 6.3 tens. We can do this again with the 0.63 that remains after this first step.0.63 × 10 ⇒ 6.3 Hundreds × 10 ⇒ Tens
So we have six tens and 0.3 tens, which is the same as 3 ones, our last place value. Now here’s the punch line. Let’s put all of the together in one place: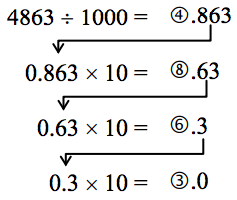 Converting from Base 10 to Base b: Another methodNote that in each step, the remainder is carried down to the next step and multiplied by 10, the base. Also, at each step, the whole number part, which is circled, gives the digit that belongs in that particular place. What is amazing is that this works for any base! So, to convert from a base 10 number to some other base, b, we have the following steps we can follow:
Converting from Base 10 to Base b: Another methodNote that in each step, the remainder is carried down to the next step and multiplied by 10, the base. Also, at each step, the whole number part, which is circled, gives the digit that belongs in that particular place. What is amazing is that this works for any base! So, to convert from a base 10 number to some other base, b, we have the following steps we can follow:
Converting from Base 10 to Base b: Another method
- Find the highest power of the base b that will divide into the given number at least once and then divide.
- Keep the whole number part, and multiply the fractional part by the base b.
- Repeat step two, keeping the whole number part (including 0), carrying the fractional part to the next step until only a whole number result is obtained.
- Collect all your whole number parts to get your number in base b notation.
Example 9
Convert the base 10 number, 34810, to base 5.Solution
This is actually a conversion that we have done in a previous example. The powers of five are:50 = 1 51 = 5 52 = 25 53 = 125 54 = 625 Etc…
The highest power of five that will go into 348 at least once is 53. We divide by 125 and then proceed.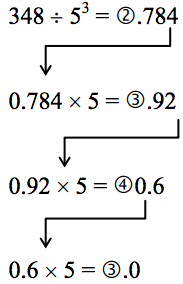 By keeping all the whole number parts, from top bottom, gives 2343 as our base 5 number. Thus, 23435 = 34810.
We can compare our result with what we saw earlier, or simply check with our calculator, and find that these two numbers really are equivalent to each other.
By keeping all the whole number parts, from top bottom, gives 2343 as our base 5 number. Thus, 23435 = 34810.
We can compare our result with what we saw earlier, or simply check with our calculator, and find that these two numbers really are equivalent to each other.
Example 10
Convert the base 10 number, 300710, to base 5.Solution
The highest power of 5 that divides at least once into 3007 is 54 = 625. Thus, we have:3007 ÷ 625 = ④.8112 0.8112 × 5 = ④.056 0.056 × 5 = ⓪.28 0.28 × 5 = ①0.4 0.4 × 5 = ②0.0
This gives us that 300710 = 440125. Notice that in the third line that multiplying by 5 gave us 0 for our whole number part. We don’t discard that! The zero tells us that a zero in that place. That is, there are no 52s in this number.Example 11
Convert the base 10 number, 6320110, to base 7.Solution
The powers of 7 are:70 = 1 71 = 7 72 = 49 73 = 343 74 = 2401 75 = 16807 etc…
The highest power of 7 that will divide at least once into 63201 is 75. When we do the initial division on a calculator, we get the following:63201 ÷ 75 = 3.760397453
The decimal part actually fills up the calculators display and we don’t know if it terminates at some point or perhaps even repeats down the road. So if we clear our calculator at this point, we will introduce error that is likely to keep this process from ever ending. To avoid this problem, we leave the result in the calculator and simply subtract 3 from this to get the fractional part all by itself. Do not round off! Subtraction and then multiplication by seven gives:63201 ÷ 75 = ③.760397453 0.760397453 × 7 = ⑤.322782174 0.322782174 × 7 = ②.259475219 0.259475219 × 7 = ①.816326531 0.816326531 × 7 = ⑤ .714285714 0.714285714 × 7 = ⑤.000000000
Yes, believe it or not, that last product is exactly 5, as long as you don’t clear anything out on your calculator. This gives us our final result: 6320110 = 3521557. If we round, even to two decimal places in each step, clearing our calculator out at each step along the way, we will get a series of numbers that do not terminate, but begin repeating themselves endlessly. (Try it!) We end up with something that doesn’t make any sense, at least not in this context. So be careful to use your calculator cautiously on these conversion problems. Also, remember that if your first division is by 75, then you expect to have 6 digits in the final answer, corresponding to the places for 75, 74, and so on down to 70. If you find yourself with more than 6 digits due to rounding errors, you know something went wrong.Try It Now
Convert the base 10 number, 935210, to base 5.Try It Now
Convert the base 10 number, 1500, to base 3. Be careful not to clear your calculator on this one. Also, if you’re not careful in each step, you may not get all of the digits you’re looking for, so move slowly and with caution.The Mayan Numeral System
Background
As you might imagine, the development of a base system is an important step in making the counting process more efficient. Our own base-ten system probably arose from the fact that we have 10 fingers (including thumbs) on two hands. This is a natural development. However, other civilizations have had a variety of bases other than ten. For example, the Natives of Queensland used a base-two system, counting as follows: “one, two, two and one, two two’s, much.” Some Modern South American Tribes have a base-five system counting in this way: “one, two, three, four, hand, hand and one, hand and two,” and so on. The Babylonians used a base-sixty (sexigesimal) system. In this chapter, we wrap up with a specific example of a civilization that actually used a base system other than 10.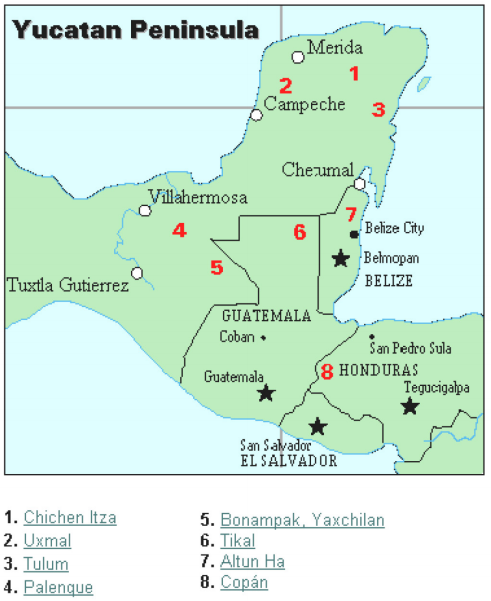 The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[footnote]http://www.gorp.com/gorp/location/latamer/map_maya.htm[/footnote]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[footnote]Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762–68.[/footnote] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[footnote]http://www.gorp.com/gorp/location/latamer/map_maya.htm[/footnote]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[footnote]Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762–68.[/footnote] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
 There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] like the sample to the left[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] like the sample to the left[footnote]http://www.ukans.edu/~lctls/Mayan/numbers.html[/footnote] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
| Powers | Base-Ten Value | Place Name |
| 207 | 12,800,000,000 | Hablat |
| 206 | 64,000,000 | Alau |
| 205 | 3,200,000 | Kinchil |
| 204 | 160,000 | Cabal |
| 203 | 8,000 | Pic |
| 202 | 400 | Bak |
| 201 | 20 | Kal |
| 200 | 1 | Hun |
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system. As we stated earlier, the Mayans used a base-20 system, called the “vigesimal” system. Like our system, it is positional, meaning that the position of a numeric symbol indicates its place value. In the following table you can see the place value in its vertical format.[footnote]Bidwell[/footnote]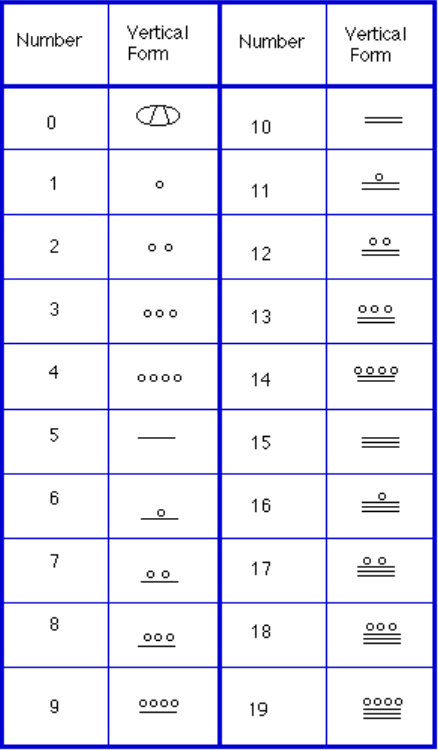 In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[footnote]http://www.vpds.wsu.edu/fair_95/gym/UM001.html[/footnote]
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[footnote]http://www.vpds.wsu.edu/fair_95/gym/UM001.html[/footnote]
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
Example 12
What is the value of this number, which is shown in vertical form?Solution
Starting from the bottom, we have the ones place. There are two bars and three dots in this place. Since each bar is worth 5, we have 13 ones when we count the three dots in the ones place. Looking to the place value above it (the twenties places), we see there are three dots so we have three twenties.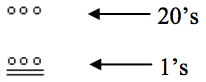 Hence we can write this number in base-ten as:
(3 × 201) + (13 × 200) = (3 × 201) + (13 × 1) = 60 + 13 = 73
Hence we can write this number in base-ten as:
(3 × 201) + (13 × 200) = (3 × 201) + (13 × 1) = 60 + 13 = 73
Example 13
What is the value of the following Mayan number?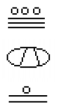
Solution
This number has 11 in the ones place, zero in the 20s place, and 18 in the 202 = 400s place. Hence, the value of this number in base-ten is: 18 × 400 + 0 × 20 + 11 × 1 = 7211.Try It Now
Convert the Mayan number below to base 10.
Example 14
Convert the base 10 number 357510 to Mayan numerals. This problem is done in two stages. First we need to convert to a base 20 number. We will do so using the method provided in the last section of the text. The second step is to convert that number to Mayan symbols. The highest power of 20 that will divide into 3575 is 202 = 400, so we start by dividing that and then proceed from there:3575 ÷ 400 = 8.9375 0.9375 × 20 = 18.75 0.75 × 20 = 15.0
This means that 357510 = 8,18,1520 The second step is to convert this to Mayan notation. This number indicates that we have 15 in the ones position. That’s three bars at the bottom of the number. We also have 18 in the 20s place, so that’s three bars and three dots in the second position. Finally, we have 8 in the 400s place, so that’s one bar and three dots on the top. We get the following:
Writing numbers with bases bigger than 10
When the base of a number is larger than 10, separate each “digit” with a comma to make the separation of digits clear. For example, in base 20, to write the number corresponding to 17 × 202 + 6 × 201 + 13 × 200, we’d write 17,6,1320.Try It Now
Convert the base 10 number 1055310 to Mayan numerals.Try It Now
Convert the base 10 number 561710 to Mayan numerals.Adding Mayan Numbers
When adding Mayan numbers together, we’ll adopt a scheme that the Mayans probably did not use but which will make life a little easier for us.Example 15
Add, in Mayan, the numbers 37 and 29:[footnote]http://forum.swarthmore.edu/k12/mayan.math/mayan2.html[/footnote]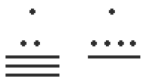 First draw a box around each of the vertical places. This will help keep the place values from being mixed up.
First draw a box around each of the vertical places. This will help keep the place values from being mixed up.
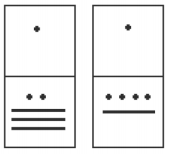 Next, put all of the symbols from both numbers into a single set of places (boxes), and to the right of this new number draw a set of empty boxes where you will place the final sum:
Next, put all of the symbols from both numbers into a single set of places (boxes), and to the right of this new number draw a set of empty boxes where you will place the final sum:
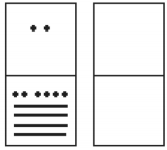 You are now ready to start carrying. Begin with the place that has the lowest value, just as you do with Arabic numbers. Start at the bottom place, where each dot is worth 1. There are six dots, but a maximum of four are allowed in any one place; once you get to five dots, you must convert to a bar. Since five dots make one bar, we draw a bar through five of the dots, leaving us with one dot which is under the four-dot limit. Put this dot into the bottom place of the empty set of boxes you just drew:
You are now ready to start carrying. Begin with the place that has the lowest value, just as you do with Arabic numbers. Start at the bottom place, where each dot is worth 1. There are six dots, but a maximum of four are allowed in any one place; once you get to five dots, you must convert to a bar. Since five dots make one bar, we draw a bar through five of the dots, leaving us with one dot which is under the four-dot limit. Put this dot into the bottom place of the empty set of boxes you just drew:
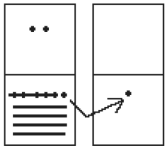 Now look at the bars in the bottom place. There are five, and the maximum number the place can hold is three. Four bars are equal to one dot in the next highest place.
Whenever we have four bars in a single place we will automatically convert that to a dot in the next place up. We draw a circle around four of the bars and an arrow up to the dots' section of the higher place. At the end of that arrow, draw a new dot. That dot represents 20 just the same as the other dots in that place. Not counting the circled bars in the bottom place, there is one bar left. One bar is under the three-bar limit; put it under the dot in the set of empty places to the right.
Now look at the bars in the bottom place. There are five, and the maximum number the place can hold is three. Four bars are equal to one dot in the next highest place.
Whenever we have four bars in a single place we will automatically convert that to a dot in the next place up. We draw a circle around four of the bars and an arrow up to the dots' section of the higher place. At the end of that arrow, draw a new dot. That dot represents 20 just the same as the other dots in that place. Not counting the circled bars in the bottom place, there is one bar left. One bar is under the three-bar limit; put it under the dot in the set of empty places to the right.
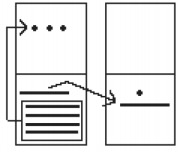 Now there are only three dots in the next highest place, so draw them in the corresponding empty box.
Now there are only three dots in the next highest place, so draw them in the corresponding empty box.
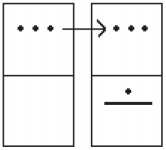 We can see here that we have 3 twenties (60), and 6 ones, for a total of 66. We check and note that 37 + 29 = 66, so we have done this addition correctly. Is it easier to just do it in base-ten? Probably, but that’s only because it’s more familiar to you. Your task here is to try to learn a new base system and how addition can be done in slightly different ways than what you have seen in the past. Note, however, that the concept of carrying is still used, just as it is in our own addition algorithm.
We can see here that we have 3 twenties (60), and 6 ones, for a total of 66. We check and note that 37 + 29 = 66, so we have done this addition correctly. Is it easier to just do it in base-ten? Probably, but that’s only because it’s more familiar to you. Your task here is to try to learn a new base system and how addition can be done in slightly different ways than what you have seen in the past. Note, however, that the concept of carrying is still used, just as it is in our own addition algorithm.
