Polynomial Equations
9.3 Learning Objectives
- Polynomial Equations
- Use factoring methods to factor polynomial equations
- Use the principle of zero products to solve polynomial equations
- Projectiles
-
- Define projectile motion
- Solve a polynomial function that represents projectile motion
- Interpret the solution to a polynomial function that represents projectile motion
- Pythagorean Theorem
-
- Recognize a right triangle from other types of triangles
- Use the Pythagorean theorem to find the lengths of a right triangle
9.3.1 The Principle of Zero Products
ZeroPrinciple of Zero Products
The Principle of Zero Products states that if the product of two numbers is 0, then at least one of the factors is 0. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are 0.Example 9.3.A
Solve: [latex-display]-t^2+t=0[/latex-display]Answer: Each term has a common factor of t, so we can factor and use the zero product principle. Rewrite each term as the product of the GCF and the remaining terms. [latex-display]\begin{array}{c}-t^2=t\left(-t\right)\\t=t\left(1\right)\end{array}[/latex-display] Rewrite the polynomial equation using the factored terms in place of the original terms.
[latex]\begin{array}{c}-t^2+t=0\\t\left(-t\right)+t\left(1\right)\\t\left(-t+1\right)=0\end{array}[/latex]
Now we have a product on one side and zero on the other, so we can set each factor equal to zero using the zero product principle.
[latex]\begin{array}{c}t=0\,\,\,\,\,\,\,\,\text{ OR }\,\,\,\,\,\,\,\,\,\,\,-t+1=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-1}\,\,\,\underline{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-t=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-t}{-1}=\frac{-1}{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=1\end{array}[/latex]
Answer
[latex-display]t=0\text{ OR }t=1[/latex-display]Example 9.3.B
Solve:[latex]s^2-4s=5[/latex]Answer: First, move all the terms to one side. The goal is to try and see if we can use the zero product principle, since that is the only tool we know for solving polynomial equations.
[latex]\begin{array}{c}\,\,\,\,\,\,\,s^2-4s=5\\\,\,\,\,\,\,\,s^2-4s-5=0\\\end{array}[/latex]
We now have all the terms on the left side, and zero on the other side. The polynomial[latex]s^2-4s-5[/latex] factors nicely, which makes this equation a good candidate for the zero product principle. (imagine that)
[latex]\begin{array}{c}s^2-4s-5=0\\\left(s+1\right)\left(s-5\right)=0\end{array}[/latex]
We separate our factors into two linear equations using the principle of zero products.
[latex-display]\begin{array}{c}\left(s-5\right)=0\\s-5=0\\\,\,\,\,\,\,\,\,\,s=5\end{array}[/latex-display] OR [latex-display]\begin{array}{c}\left(s+1\right)=0\\s+1=0\\s=-1\end{array}[/latex-display]Answer
[latex-display]s=-1\text{ OR }s=5[/latex-display]Example 9.3.C
Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]Answer: We can solve this in one of two ways. One way is to eliminate the fractions like you may have done when solving linear equations, and the second is to find a common denominator and factor fractions. Eliminating fractions is easier, so we will show that way. Start by multiplying the whole equation by 2 to eliminate fractions: [latex-display]\begin{array}{ccc}2\left(y^2-5=-\frac{7}{2}y+\frac{5}{2}\right)\\\,\,\,\,\,\,2(y^2)+2(-5)=2\left(-\frac{7}{2}\right)+2\left(\frac{5}{2}\right)\\2y^2-10=-7y+5\end{array}[/latex-display] Now we can move all the terms to one side and see if this will factor so we can use the principle of zero products. [latex-display]\begin{array}{c}2y^2-10=-7y+5\\2y^2-10+7y-5=0\\2y^2-15+7y=0\\2y^2+7y-15=0\end{array}[/latex-display] We can now check whether this polynomial will factor, using a table we can list factors until we find two numbers with a product of [latex]2\cdot-15=-30[/latex] and a sum of 7.
| Factors of [latex]2\cdot-15=-30[/latex] | Sum of Factors |
|---|---|
| [latex]1,-30[/latex] | [latex]-29[/latex] |
| [latex]-1,30[/latex] | [latex]29[/latex] |
| [latex]2,-15[/latex] | [latex]-13[/latex] |
| [latex]-2,15[/latex] | [latex]13[/latex] |
| [latex]3,-10[/latex] | [latex]-7[/latex] |
| [latex]-3,10[/latex] | [latex]7[/latex] |
Answer
[latex]y=\frac{3}{2}\text{ OR }y=-5[/latex]
9.3.2 Projectile Motion
Projectile motion happens when you throw a ball into the air and it comes back down because of gravity. A projectile will follow a curved path that behaves in a predictable way. This predictable motion has been studied for centuries, and in simple cases it's height from the ground at a given time, t, can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where h(t) = height of an object at a given time, t. Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile's motion, as in the image of water in the fountain below.
Parabolic WaterTrajectoryExample 9.3.d
A small toy rocket is launched from a 4-foot pedestal. The height (h, in feet) of the rocket t seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?Answer: The rocket will be on the ground when the [latex]h(t)=0[/latex]. We want to know how long, t, the rocket is in the air. [latex-display]\begin{array}{l}h(t)=−2t^{2}+7t+4=0\\0=−2t^{2}+7t+4\end{array}[/latex-display] We can factor the polynomial [latex]−2t^{2}+7t+4[/latex] more easily by first factoring out a [latex]-1[/latex] [latex-display]\begin{array}{c}0=-1(2t^{2}-7t-4)\\0=-1\left(2t+1\right)\left(t-4\right)\end{array}[/latex-display] Use the Zero Product Property. There is no need to set the constant factor [latex]-1[/latex] to zero, because [latex]-1[/latex] will never equal zero.
[latex]2t+1=0\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t-4=0[/latex]
Solve each equation.[latex]t=-\frac{1}{2}\,\,\,\,\,\,\text{or}\,\,\,\,\,\,t=4[/latex]
Interpret the answer. Since t represents time, it cannot be a negative number; only [latex]t=4[/latex] makes sense in this context. [latex-display]t=4[/latex-display] We can check our answer: [latex]\begin{array}{c}h(4)=−2(4)^{2}+7(4)+4=0\\h(4)=-2(16)+28+4=0\\h(4)-32+32=0\\h(4)=0\end{array}[/latex]Answer
The rocket will hit the ground 4 seconds after being launched.Example 9.3.e
Use the formula for the height of the rocket in the previous example to find the time when the rocket is 4 feet from hitting the ground on it's way back down. Refer to the image. [latex-display]h(t)=−2t^{2}+7t+4[/latex-display]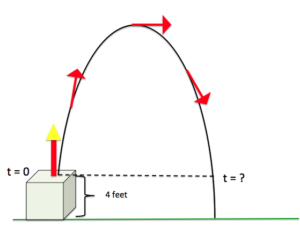
Answer: We are given that the height of the rocket is 4 feet from the ground on it's way back down. We want to know how long it has taken the rocket to get to that point in it's path, we are going to solve for t. Substitute [latex]h(t) = 4[/latex] into the formula for height, and try to get zero on one side since we know we can use the zero product principle to solve polynomials. Write and Solve:
[latex]\begin{array}{l}h(t)=4=−2t^{2}+7t+4\\4=-2t^2+7t+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\0=-2t^2+7t\end{array}[/latex]
Now we can factor out a t from each term:
[latex]0=t\left(-2t+7\right)[/latex]
Solve each equation for t using the zero product principle:
[latex]\begin{array}{l}t=0\text{ OR }-2t+7=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-7}\,\,\,\,\,\,\,\underline{-7}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-2t}{-2}=\frac{-7}{-2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=\frac{7}{2}=3.5\end{array}[/latex]
It doesn't make sense for us to choose t=0 because we are interested in the amount of time that has passed when the projectile is 4 feet from hitting the ground on it's way back down. We will choose t=3.5
Check the answer on your own for practice.
Answer
[latex-display]t=3.5\text{ seconds }[/latex-display]9.3.3 Pythagorean Theorem
Triangles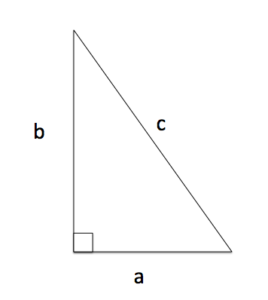
Right Triangle LabeledThe Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the longest leg of a right triangle is labeled c, and the other two a, and b as in the image on teh left, The Pythagorean Theorem states that
[latex]a^2+b^2=c^2[/latex]
Given enough information, we can solve for an unknown length. This relationship has been used for many, many years for things such as celestial navigation and early civil engineering projects. We now have digital GPS and survey equipment that have been programmed to do the calculations for us.
In the next example we will combine the power of the Pythagorean theorem and what we know about solving quadratic equations to find unknown lengths of right triangles.
Example 9.3.f
A right triangle has one leg with length x, another whose length is greater by two, and the length of the hypotenuse is greater by four. Find the lengths of the sides of the triangle. Use the image below.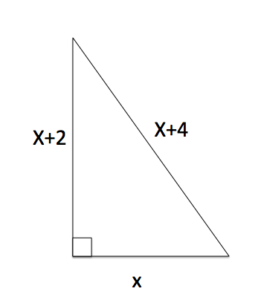
Answer: Read and understand: We know the lengths of all the sides of a triangle in terms of one side. We also know that the Pythagorean theorem will give us a relationship between the side lengths of a right triangle. Translate:
[latex]\begin{array}{l}a^2+b^2=c^2\\x^2+\left(x+2\right)^2=\left(x+4\right)^2\end{array}[/latex]
Solve: If we can move all the terms to one side and factor, we can use the zero product principle to solve. Since this is the only method we know - let's hope it works! First, multiply the binomials and simplify so we can see what we are working with.[latex]\begin{array}{l}x^2+\left(x+2\right)^2=\left(x+4\right)^2\\x^2+x^2+4x+4=x^2+8x+16\\2x^2+4x+4=x^2+8x+16\end{array}[/latex]
Now move all the terms to one side and see if we can factor.
[latex]\begin{array}{l}2x^2+4x+4=x^2+8x+16\\\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\,\,\,\,\,\underline{-x^2}\,\,\,\underline{-8x}\,\,\,\underline{-16}\\x^2-4x-12=0\end{array}[/latex]
This went from a messy looking problem to something promising. We can factor using the shortcut:
[latex]-6\cdot{2}=-12,\text{ and }-6+2=-4[/latex]
So we can build our binomial factors with -6 and 2:
[latex]\left(x-6\right)\left(x+2\right)=0[/latex]
Set each factor equal to zero:
[latex]x-6=0, x=6[/latex]
[latex]x+2=0, x=-2[/latex]
Interpret: Ok, it doesn't make sense to have a length equal to -2, so we can safely throw that solution out. The lengths of the sides are as follows:
[latex]x=6[/latex]
[latex]x+2=6+2=8[/latex]
[latex]x+4=6+4=10[/latex]
Check: Since we know the relationship between the sides of a right triangle we can check that we are correct. Sometimes it helps to draw a picture
.
We know that [latex]a^2+b^2=c^2[/latex], so we can substitute the values we found:
[latex]\begin{array}{l}6^2+8^2=10^2\\36+64=100\\100=100\end{array}[/latex]
Our solution checks out.
Answer
The lengths of the sides of the right triangle are 6, 8, and 10Licenses & Attributions
CC licensed content, Original
- Solve a Quadratic Equations with Fractions by Factoring (a not 1). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Parabolic motion description and example. Provided by: Lumen Learning License: CC BY: Attribution.
- Factoring Application - Find the Time When a Projectile Hits and Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Pythagorean Theorem, Description and Examples. Provided by: Lumen Learning License: CC BY: Attribution.
- Screenshot: Thumbsdown. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: Factor and Solve Quadratic Equation - Greatest Common Factor Only. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Factor and Solve Quadratic Equations When A equals 1. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Parabolic water trajectory. Authored by: By GuidoB. Located at: https://commons.wikimedia.org/w/index.php?curid=8015696. License: CC BY-SA: Attribution-ShareAlike.
- Celestial Navigation Math. Authored by: TabletClass Math. License: All Rights Reserved. License terms: Standard YouTube License.
- Pythagorean Theorem. Provided by: Wikipedia Located at: https://en.wikipedia.org/wiki/Pythagorean_theorem. License: CC BY-SA: Attribution-ShareAlike.
