Solutions
Solutions to Try Its
1. [latex]{f}^{-1}\left(f\left(x\right)\right)={f}^{-1}\left(\frac{x+5}{3}\right)=3\left(\frac{x+5}{3}\right)-5=\left(x - 5\right)+5=x[/latex] and [latex]f\left({f}^{-1}\left(x\right)\right)=f\left(3x - 5\right)=\frac{\left(3x - 5\right)+5}{3}=\frac{3x}{3}=x[/latex] 2. [latex]{f}^{-1}\left(x\right)={x}^{3}-4[/latex] 3. [latex]{f}^{-1}\left(x\right)=\sqrt{x - 1}[/latex] 4. [latex]{f}^{-1}\left(x\right)=\frac{{x}^{2}-3}{2},x\ge 0[/latex] 5. [latex]{f}^{-1}\left(x\right)=\frac{2x+3}{x - 1}[/latex]Solutions to Odd-Numbered Exercises
1. It can be too difficult or impossible to solve for x in terms of y. 3. We will need a restriction on the domain of the answer. 5. [latex]{f}^{-1}\left(x\right)=\sqrt{x}+4[/latex] 7. [latex]{f}^{-1}\left(x\right)=\sqrt{x+3}-1[/latex] 9. [latex]{f}^{-1}\left(x\right)=-\sqrt{\frac{x - 5}{3}}[/latex] 11. [latex]f\left(x\right)=\sqrt{9-x}[/latex] 13. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{x - 5}[/latex] 15. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{4-x}[/latex] 17. [latex]{f}^{-1}\left(x\right)=\frac{{x}^{2}-1}{2},\left[0,\infty \right)[/latex] 19. [latex]{f}^{-1}\left(x\right)=\frac{{\left(x - 9\right)}^{2}+4}{4},\left[9,\infty \right)[/latex] 21. [latex]{f}^{-1}\left(x\right)={\left(\frac{x - 9}{2}\right)}^{3}[/latex] 23. [latex]{f}^{-1}\left(x\right)={\frac{2 - 8x}{x}}[/latex] 25. [latex]{f}^{-1}\left(x\right)=\frac{7x - 3}{1-x}[/latex] 27. [latex]{f}^{-1}\left(x\right)=\frac{5x - 4}{4x+3}[/latex] 29. [latex]{f}^{-1}\left(x\right)=\sqrt{x+1}-1[/latex] 31. [latex]{f}^{-1}\left(x\right)=\sqrt{x+6}+3[/latex] 33. [latex]{f}^{-1}\left(x\right)=\sqrt{4-x}[/latex] 35. [latex]{f}^{-1}\left(x\right)=\sqrt{x}+4[/latex]
35. [latex]{f}^{-1}\left(x\right)=\sqrt{x}+4[/latex]
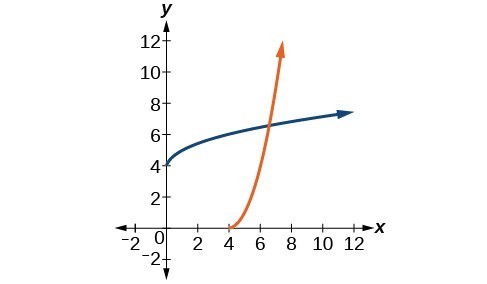 37. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{1-x}[/latex]
37. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{1-x}[/latex]
 39. [latex]{f}^{-1}\left(x\right)=\sqrt{x+8}+3[/latex]
39. [latex]{f}^{-1}\left(x\right)=\sqrt{x+8}+3[/latex]
 41. [latex]{f}^{-1}\left(x\right)=\sqrt{\frac{1}{x}}[/latex]
41. [latex]{f}^{-1}\left(x\right)=\sqrt{\frac{1}{x}}[/latex]
 43. [latex]\left[-2,1\right)\cup \left[3,\infty \right)[/latex]
43. [latex]\left[-2,1\right)\cup \left[3,\infty \right)[/latex]
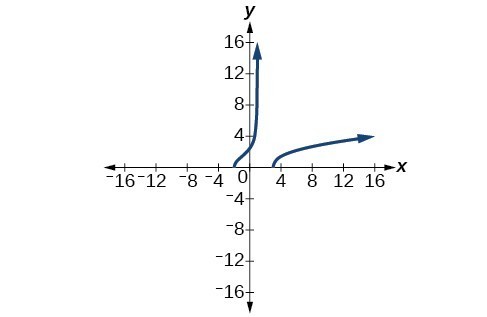 45. [latex]\left[-4,2\right)\cup \left[5,\infty \right)[/latex]
45. [latex]\left[-4,2\right)\cup \left[5,\infty \right)[/latex]
 47. [latex]\left(-2, 0\right); \left(4, 2\right); \left(22, 3\right)[/latex]
47. [latex]\left(-2, 0\right); \left(4, 2\right); \left(22, 3\right)[/latex]
 49. [latex]\left(-4, 0\right); \left(0, 1\right); \left(10, 2\right)[/latex]
49. [latex]\left(-4, 0\right); \left(0, 1\right); \left(10, 2\right)[/latex]
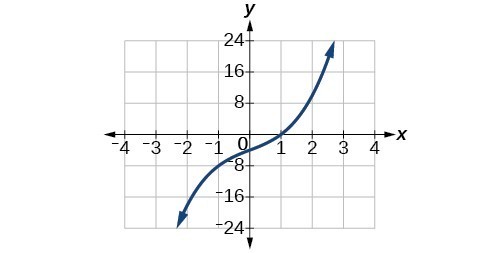 51. [latex]\left(-3, -1\right); \left(1, 0\right); \left(7, 1\right)[/latex]
51. [latex]\left(-3, -1\right); \left(1, 0\right); \left(7, 1\right)[/latex]
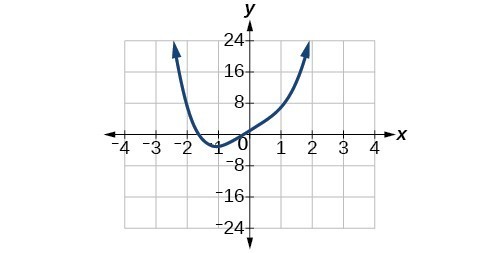 53. [latex]{f}^{-1}\left(x\right)=\sqrt{x+\frac{{b}^{2}}{4}}-\frac{b}{2}[/latex]
55. [latex]{f}^{-1}\left(x\right)=\frac{{x}^{3}-b}{a}[/latex]
57. [latex]t\left(h\right)=\sqrt{\frac{200-h}{4.9}}[/latex], 5.53 seconds
59. [latex]r\left(V\right)=\sqrt[3]{\frac{3V}{4\pi }}[/latex], 3.63 feet
61. [latex]n\left(C\right)=\frac{100C - 25}{.6-C}[/latex], 250 mL
63. [latex]r\left(V\right)=\sqrt{\frac{V}{6\pi }}[/latex], 3.99 meters
65. [latex]r\left(V\right)=\sqrt{\frac{V}{4\pi }}[/latex], 1.99 inches
53. [latex]{f}^{-1}\left(x\right)=\sqrt{x+\frac{{b}^{2}}{4}}-\frac{b}{2}[/latex]
55. [latex]{f}^{-1}\left(x\right)=\frac{{x}^{3}-b}{a}[/latex]
57. [latex]t\left(h\right)=\sqrt{\frac{200-h}{4.9}}[/latex], 5.53 seconds
59. [latex]r\left(V\right)=\sqrt[3]{\frac{3V}{4\pi }}[/latex], 3.63 feet
61. [latex]n\left(C\right)=\frac{100C - 25}{.6-C}[/latex], 250 mL
63. [latex]r\left(V\right)=\sqrt{\frac{V}{6\pi }}[/latex], 3.99 meters
65. [latex]r\left(V\right)=\sqrt{\frac{V}{4\pi }}[/latex], 1.99 inchesLicenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
