Complex Numbers
The study of mathematics continuously builds upon itself. Negative integers, for example, fill a void left by the set of positive integers. The set of rational numbers, in turn, fills a void left by the set of integers. The set of real numbers fills a void left by the set of rational numbers. Not surprisingly, the set of real numbers has voids as well. For example, we still have no solution to equations such as[latex]{x}^{2}+4=0[/latex]
Our best guesses might be +2 or –2. But if we test +2 in this equation, it does not work. If we test –2, it does not work. If we want to have a solution for this equation, we will have to go farther than we have so far. After all, to this point we have described the square root of a negative number as undefined. Fortunately, there is another system of numbers that provides solutions to problems such as these. In this section, we will explore this number system and how to work within it.Express and Plot Complex Numbers
We know how to find the square root of any positive real number. In a similar way, we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number [latex]i[/latex] is defined as the square root of negative 1.[latex]\sqrt{-1}=i[/latex]
So, using properties of radicals,[latex]{i}^{2}={\left(\sqrt{-1}\right)}^{2}=-1[/latex]
We can write the square root of any negative number as a multiple of i. Consider the square root of –25.[latex]\begin{array}{l} \sqrt{-25}=\sqrt{25\cdot \left(-1\right)}\hfill \\ \text{ }=\sqrt{25}\sqrt{-1}\hfill \\ \text{ }=5i\hfill \end{array}[/latex]
We use 5i and not [latex]-\text{5}i[/latex] because the principal root of 25 is the positive root.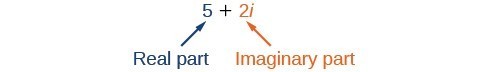
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written a + bi where a is the real part and bi is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex].
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.
A General Note: Imaginary and Complex Numbers
A complex number is a number of the form [latex]a+bi[/latex] where- a is the real part of the complex number.
- bi is the imaginary part of the complex number.
How To: Given an imaginary number, express it in standard form.
- Write [latex]\sqrt{-a}[/latex] as [latex]\sqrt{a}\sqrt{-1}[/latex].
- Express [latex]\sqrt{-1}[/latex] as i.
- Write [latex]\sqrt{a}\cdot i[/latex] in simplest form.
Example: Expressing an Imaginary Number in Standard Form
Express [latex]\sqrt{-9}[/latex] in standard form.Answer: [latex-display]\sqrt{-9}=\sqrt{9}\sqrt{-1}=3i[/latex-display] In standard form, this is [latex]0+3i[/latex].
Try It
Express [latex]\sqrt{-24}[/latex] in standard form.Answer: [latex]\sqrt{-24}=0+2i\sqrt{6}\\[/latex]
Add, Subtract, and Multiply Complex Numbers
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and combine the imaginary parts.A General Note: Addition and Subtraction of Complex Numbers
Adding complex numbers:[latex]\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i[/latex]
Subtracting complex numbers:[latex]\left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right)i[/latex]
How To: Given two complex numbers, find the sum or difference.
- Identify the real and imaginary parts of each number.
- Add or subtract the real parts.
- Add or subtract the imaginary parts.
Example: Adding Complex Numbers
Add [latex]3 - 4i[/latex] and [latex]2+5i[/latex].Answer: We add the real parts and add the imaginary parts.
[latex]\begin{array}{l}\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i\hfill \\ \left(3 - 4i\right)+\left(2+5i\right)=\left(3+2\right)+\left(-4+5\right)i\hfill \\ \text{ }=5+i\hfill \end{array}[/latex]
Try It
Subtract [latex]2+5i[/latex] from [latex]3 - 4i[/latex].Answer: [latex]\left(3 - 4i\right)-\left(2+5i\right)=1 - 9i[/latex]
Multiplying Complex Numbers Together
Now, let’s multiply two complex numbers. We can use either the distributive property or the FOIL method. Recall that FOIL is an acronym for multiplying First, Outer, Inner, and Last terms together. Using either the distributive property or the FOIL method, we get[latex]\left(a+bi\right)\left(c+di\right)=ac+adi+bci+bd{i}^{2}[/latex]
Because [latex]{i}^{2}=-1[/latex], we have[latex]\left(a+bi\right)\left(c+di\right)=ac+adi+bci-bd[/latex]
To simplify, we combine the real parts, and we combine the imaginary parts.[latex]\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i[/latex]
How To: Given two complex numbers, multiply to find the product.
- Use the distributive property or the FOIL method.
- Simplify.
Example: Multiplying a Complex Number by a Complex Number
Multiply [latex]\left(4+3i\right)\left(2 - 5i\right)[/latex].Answer:
Use [latex]\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i[/latex]
[latex]\begin{array}{c}\left(4+3i\right)\left(2 - 5i\right)=\left(4\cdot 2 - 3\cdot \left(-5\right)\right)+\left(4\cdot \left(-5\right)+3\cdot 2\right)i\hfill \\ =\left(8+15\right)+\left(-20+6\right)i\hfill \\ =23 - 14i\hfill \end{array}[/latex]
Try It
Multiply [latex]\left(3 - 4i\right)\left(2+3i\right)[/latex].Answer: [latex]18+i[/latex]
Example: Substituting an Imaginary Number in a Rational Function
Let [latex]f\left(x\right)=\frac{2+x}{x+3}[/latex]. Evaluate [latex]f\left(10i\right)[/latex].Answer: Substitute [latex]x=10i[/latex] and simplify. [latex-display]\begin{array}{l}\frac{2+10i}{10i+3}\hfill & \text{Substitute }10i\text{ for }x.\hfill \\ \frac{2+10i}{3+10i}\hfill & \text{Rewrite the denominator in standard form}.\hfill \\ \frac{2+10i}{3+10i}\cdot \frac{3 - 10i}{3 - 10i}\hfill & \text{Prepare to multiply the numerator and}\hfill \\ \hfill & \text{denominator by the complex conjugate}\hfill \\ \hfill & \text{of the denominator}.\hfill \\ \frac{6 - 20i+30i - 100{i}^{2}}{9 - 30i+30i - 100{i}^{2}}\hfill & \text{Multiply using the distributive property or the FOIL method}.\hfill \\ \frac{6 - 20i+30i - 100\left(-1\right)}{9 - 30i+30i - 100\left(-1\right)}\hfill & \text{Substitute }-1\text{ for } {i}^{2}.\hfill \\ \frac{106+10i}{109}\hfill & \text{Simplify}.\hfill \\ \frac{106}{109}+\frac{10}{109}i\hfill & \text{Separate the real and imaginary parts}.\hfill \end{array}[/latex-display]
Try It
Let [latex]f\left(x\right)=\frac{x+1}{x - 4}[/latex]. Evaluate [latex]f\left(-i\right)[/latex].Answer: [latex]-\frac{3}{17}+\frac{5i}{17}[/latex]
Simplifying Powers of i
The powers of i are cyclic. Let’s look at what happens when we raise i to increasing powers. [latex-display]\begin{array}{l}{i}^{1}=i\\ {i}^{2}=-1\\ {i}^{3}={i}^{2}\cdot i=-1\cdot i=-i\\ {i}^{4}={i}^{3}\cdot i=-i\cdot i=-{i}^{2}=-\left(-1\right)=1\\ {i}^{5}={i}^{4}\cdot i=1\cdot i=i\end{array}[/latex-display] We can see that when we get to the fifth power of i, it is equal to the first power. As we continue to multiply i by itself for increasing powers, we will see a cycle of 4. Let’s examine the next 4 powers of i. [latex-display]\begin{array}{l}{i}^{6}={i}^{5}\cdot i=i\cdot i={i}^{2}=-1\\ {i}^{7}={i}^{6}\cdot i={i}^{2}\cdot i={i}^{3}=-i\\ {i}^{8}={i}^{7}\cdot i={i}^{3}\cdot i={i}^{4}=1\\ {i}^{9}={i}^{8}\cdot i={i}^{4}\cdot i={i}^{5}=i\end{array}[/latex-display]Example: Simplifying Powers of i
Evaluate [latex]{i}^{35}[/latex].Answer: Since [latex]{i}^{4}=1[/latex], we can simplify the problem by factoring out as many factors of [latex]{i}^{4}[/latex] as possible. To do so, first determine how many times 4 goes into 35: [latex]35=4\cdot 8+3[/latex]. [latex-display]{i}^{35}={i}^{4\cdot 8+3}={i}^{4\cdot 8}\cdot {i}^{3}={\left({i}^{4}\right)}^{8}\cdot {i}^{3}={1}^{8}\cdot {i}^{3}={i}^{3}=-i[/latex-display]
Q & A
Can we write [latex]{i}^{35}[/latex] in other helpful ways? As we saw in Example: Simplifying Powers of i, we reduced [latex]{i}^{35}[/latex] to [latex]{i}^{3}[/latex] by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of [latex]{i}^{35}[/latex] may be more useful. The table below shows some other possible factorizations.| Factorization of [latex]{i}^{35}[/latex] | [latex]{i}^{34}\cdot i[/latex] | [latex]{i}^{33}\cdot {i}^{2}[/latex] | [latex]{i}^{31}\cdot {i}^{4}[/latex] | [latex]{i}^{19}\cdot {i}^{16}[/latex] |
| Reduced form | [latex]{\left({i}^{2}\right)}^{17}\cdot i[/latex] | [latex]{i}^{33}\cdot \left(-1\right)[/latex] | [latex]{i}^{31}\cdot 1[/latex] | [latex]{i}^{19}\cdot {\left({i}^{4}\right)}^{4}[/latex] |
| Simplified form | [latex]{\left(-1\right)}^{17}\cdot i[/latex] | [latex]-{i}^{33}[/latex] | [latex]{i}^{31}[/latex] | [latex]{i}^{19}[/latex] |
Key Concepts
- The square root of any negative number can be written as a multiple of i.
- To plot a complex number, we use two number lines, crossed to form the complex plane. The horizontal axis is the real axis, and the vertical axis is the imaginary axis.
- Complex numbers can be added and subtracted by combining the real parts and combining the imaginary parts.
- Complex numbers can be multiplied and divided.
- To multiply complex numbers, distribute just as with polynomials.
- To divide complex numbers, multiply both the numerator and denominator by the complex conjugate of the denominator to eliminate the complex number from the denominator.
- The powers of i are cyclic, repeating every fourth one.
Glossary
- complex conjugate
- the complex number in which the sign of the imaginary part is changed and the real part of the number is left unchanged; when added to or multiplied by the original complex number, the result is a real number
- complex number
- the sum of a real number and an imaginary number, written in the standard form a + bi, where a is the real part, and bi is the imaginary part
- complex plane
- a coordinate system in which the horizontal axis is used to represent the real part of a complex number and the vertical axis is used to represent the imaginary part of a complex number
- imaginary number
- a number in the form bi where [latex]i=\sqrt{-1}\\[/latex]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 120193. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Introduction to Complex Numbers. Authored by: Sousa, James. License: CC BY: Attribution.
- Question ID 61706. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 65709. Authored by: Kaslik, Pete, mb Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex: Dividing Complex Numbers. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 1: Adding and Subtracting Complex Numbers. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Question ID 61710, 61715. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 40462. Authored by: Jenck, Michael. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 3903. Authored by: Lippman, David . License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex 2: Multiply Complex Numbers. Authored by: Sousa, James (Mathispower4u). License: CC BY: Attribution.
- Ex: Dividing Complex Numbers . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
