Compositions of Functions
Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.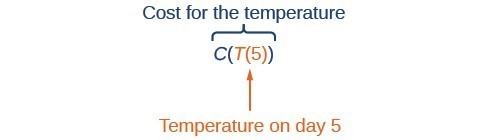
Figure 1Compositions of Functions
Function composition is only one way to combine existing functions. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.
Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. If [latex]w\left(y\right)[/latex] is the wife’s income and [latex]h\left(y\right)[/latex] is the husband’s income in year [latex]y[/latex], and we want [latex]T[/latex] to represent the total income, then we can define a new function.
If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write
Just as for this sum of two functions, we can define difference, product, and ratio functions for any pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can think of adding, subtracting, multiplying, and dividing functions.
For two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] with real number outputs, we define new functions [latex]f+g,f-g,fg[/latex], and [latex]\frac{f}{g}[/latex] by the relations
Example: Performing Algebraic Operations on Functions
Find and simplify the functions [latex]\left(g-f\right)\left(x\right)[/latex] and [latex]\left(\frac{g}{f}\right)\left(x\right)[/latex], given [latex]f\left(x\right)=x - 1[/latex] and [latex]g\left(x\right)={x}^{2}-1[/latex]. Give the domain of your result. Are they the same function?Answer:
Begin by writing the general form, and then substitute the given functions.
No, the functions are not the same.
Note: For [latex]\left(\frac{g}{f}\right)\left(x\right)[/latex], the condition [latex]x\ne 1[/latex] is necessary because when [latex]x=1[/latex], the denominator is equal to 0, which makes the function undefined.
Try It
Find and simplify the functions [latex]\left(fg\right)\left(x\right)[/latex] and [latex]\left(f-g\right)\left(x\right)[/latex].Are they the same function?
Answer: [latex]\begin{array}{c}\left(fg\right)\left(x\right)=f\left(x\right)g\left(x\right)=\left(x - 1\right)\left({x}^{2}-1\right)={x}^{3}-{x}^{2}-x+1\\ \left(f-g\right)\left(x\right)=f\left(x\right)-g\left(x\right)=\left(x - 1\right)-\left({x}^{2}-1\right)=x-{x}^{2}\end{array}[/latex] No, the functions are not the same.
Example: Interpreting Composite Functions
The function [latex]c\left(s\right)[/latex] gives the number of calories burned completing [latex]s[/latex] sit-ups, and [latex]s\left(t\right)[/latex] gives the number of sit-ups a person can complete in [latex]t[/latex] minutes. Interpret [latex]c\left(s\left(3\right)\right)[/latex].Answer: The inside expression in the composition is [latex]s\left(3\right)[/latex]. Because the input to the s-function is time, [latex]t=3[/latex] represents 3 minutes, and [latex]s\left(3\right)[/latex] is the number of sit-ups completed in 3 minutes. Using [latex]s\left(3\right)[/latex] as the input to the function [latex]c\left(s\right)[/latex] gives us the number of calories burned during the number of sit-ups that can be completed in 3 minutes, or simply the number of calories burned in 3 minutes (by doing sit-ups).
Example: Investigating the Order of Function Composition
Suppose [latex]f\left(x\right)[/latex] gives miles that can be driven in [latex]x[/latex] hours and [latex]g\left(y\right)[/latex] gives the gallons of gas used in driving [latex]y[/latex] miles. Which of these expressions is meaningful: [latex]f\left(g\left(y\right)\right)[/latex] or [latex]g\left(f\left(x\right)\right)?[/latex]Answer: The function [latex]y=f\left(x\right)[/latex] is a function whose output is the number of miles driven corresponding to the number of hours driven. [latex-display]\text{number of miles }=f\left(\text{number of hours}\right)[/latex-display] The function [latex]g\left(y\right)[/latex] is a function whose output is the number of gallons used corresponding to the number of miles driven. This means: [latex-display]\text{number of gallons }=g\left(\text{number of miles}\right)[/latex-display] The expression [latex]g\left(y\right)[/latex] takes miles as the input and a number of gallons as the output. The function [latex]f\left(x\right)[/latex] requires a number of hours as the input. Trying to input a number of gallons does not make sense. The expression [latex]f\left(g\left(y\right)\right)[/latex] is meaningless. The expression [latex]f\left(x\right)[/latex] takes hours as input and a number of miles driven as the output. The function [latex]g\left(y\right)[/latex] requires a number of miles as the input. Using [latex]f\left(x\right)[/latex] (miles driven) as an input value for [latex]g\left(y\right)[/latex], where gallons of gas depends on miles driven, does make sense. The expression [latex]g\left(f\left(x\right)\right)[/latex] makes sense, and will yield the number of gallons of gas used, [latex]g[/latex], driving a certain number of miles, [latex]f\left(x\right)[/latex], in [latex]x[/latex] hours.
Evaluate a Composition of Functions
Once we compose a new function from two existing functions, we need to be able to evaluate it for any input in its domain. We will do this with specific numerical inputs for functions expressed as tables, graphs, and formulas and with variables as inputs to functions expressed as formulas. In each case, we evaluate the inner function using the starting input and then use the inner function’s output as the input for the outer function.Evaluating Composite Functions Using Tables
When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.Example: Using a Table to Evaluate a Composite Function
Using the table below, evaluate [latex]f\left(g\left(3\right)\right)[/latex] and [latex]g\left(f\left(3\right)\right)[/latex].| [latex]x[/latex] | [latex]f\left(x\right)[/latex] | [latex]g\left(x\right)[/latex] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Answer: To evaluate [latex]f\left(g\left(3\right)\right)[/latex], we start from the inside with the input value 3. We then evaluate the inside expression [latex]g\left(3\right)[/latex] using the table that defines the function [latex]g:[/latex] [latex]g\left(3\right)=2[/latex]. We can then use that result as the input to the function [latex]f[/latex], so [latex]g\left(3\right)[/latex] is replaced by 2 and we get [latex]f\left(2\right)[/latex]. Then, using the table that defines the function [latex]f[/latex], we find that [latex]f\left(2\right)=8[/latex].
[latex]\begin{array}{l}g\left(3\right)=2\hfill \\ f\left(g\left(3\right)\right)=f\left(2\right)=8\hfill \end{array}[/latex]
To evaluate [latex]g\left(f\left(3\right)\right)[/latex], we first evaluate the inside expression [latex]f\left(3\right)[/latex] using the first table: [latex]f\left(3\right)=3[/latex]. Then, using the table for [latex]g\text{,\hspace{0.17em}}[/latex] we can evaluate[latex]g\left(f\left(3\right)\right)=g\left(3\right)=2[/latex]
The table below shows the composite functions [latex]f\circ g[/latex] and [latex]g\circ f[/latex] as tables.| [latex]x[/latex] | [latex]g\left(x\right)[/latex] | [latex]f\left(g\left(x\right)\right)[/latex] | [latex]f\left(x\right)[/latex] | [latex]g\left(f\left(x\right)\right)[/latex] |
| 3 | 2 | 8 | 3 | 2 |
Try It
Using the table below, evaluate [latex]f\left(g\left(1\right)\right)[/latex] and [latex]g\left(f\left(4\right)\right)[/latex].| [latex]x[/latex] | [latex]f\left(x\right)[/latex] | [latex]g\left(x\right)[/latex] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Answer: [latex-display]f\left(g\left(1\right)\right)=f\left(3\right)=3[/latex] and [latex]g\left(f\left(4\right)\right)=g\left(1\right)=3[/latex-display]
Evaluating Composite Functions Using Formulas
When evaluating a composite function where we have either created or been given formulas, the rule of working from the inside out remains the same. The input value to the outer function will be the output of the inner function, which may be a numerical value, a variable name, or a more complicated expression. While we can compose the functions for each individual input value, it is sometimes helpful to find a single formula that will calculate the result of a composition [latex]f\left(g\left(x\right)\right)[/latex]. To do this, we will extend our idea of function evaluation. Recall that, when we evaluate a function like [latex]f\left(t\right)={t}^{2}-t[/latex], we substitute the value inside the parentheses into the formula wherever we see the input variable.How To: Given a formula for a composite function, evaluate the function.
- Evaluate the inside function using the input value or variable provided.
- Use the resulting output as the input to the outside function.
Example: Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input
Given [latex]f\left(t\right)={t}^{2}-{t}[/latex] and [latex]h\left(x\right)=3x+2[/latex], evaluate [latex]f\left(h\left(1\right)\right)[/latex].Answer: Because the inside expression is [latex]h\left(1\right)[/latex], we start by evaluating [latex]h\left(x\right)[/latex] at 1.
[latex]\begin{array}{l}h\left(1\right)=3\left(1\right)+2\\ h\left(1\right)=5\end{array}[/latex]
Then [latex]f\left(h\left(1\right)\right)=f\left(5\right)[/latex], so we evaluate [latex]f\left(t\right)[/latex] at an input of 5.[latex]\begin{array}{l}f\left(h\left(1\right)\right)=f\left(5\right)\\ f\left(h\left(1\right)\right)={5}^{2}-5\\ f\left(h\left(1\right)\right)=20\end{array}[/latex]
Analysis of the Solution
It makes no difference what the input variables [latex]t[/latex] and [latex]x[/latex] were called in this problem because we evaluated for specific numerical values.Try It
Given [latex]f\left(t\right)={t}^{2}-t[/latex] and [latex]h\left(x\right)=3x+2[/latex], evaluate A) [latex]h\left(f\left(2\right)\right)[/latex] B) [latex]h\left(f\left(-2\right)\right)[/latex]Answer: A. 8; B. 20
Decompose a Composite Function
In some cases, it is necessary to decompose a complicated function. In other words, we can write it as a composition of two simpler functions. There may be more than one way to decompose a composite function, so we may choose the decomposition that appears to be most expedient.Example: Decomposing a Function
Write [latex]f\left(x\right)=\sqrt{5-{x}^{2}}[/latex] as the composition of two functions.Answer: We are looking for two functions, [latex]g[/latex] and [latex]h[/latex], so [latex]f\left(x\right)=g\left(h\left(x\right)\right)[/latex]. To do this, we look for a function inside a function in the formula for [latex]f\left(x\right)[/latex]. As one possibility, we might notice that the expression [latex]5-{x}^{2}[/latex] is the inside of the square root. We could then decompose the function as
[latex]h\left(x\right)=5-{x}^{2}\text{ and }g\left(x\right)=\sqrt{x}[/latex]
We can check our answer by recomposing the functions.[latex]g\left(h\left(x\right)\right)=g\left(5-{x}^{2}\right)=\sqrt{5-{x}^{2}}[/latex]
Try It
Write [latex]f\left(x\right)=\frac{4}{3-\sqrt{4+{x}^{2}}}[/latex] as the composition of two functions.Answer: Possible answer:
[latex]g\left(x\right)=\sqrt{4+{x}^{2}}[/latex]
[latex-display]h\left(x\right)=\frac{4}{3-x}[/latex-display] [latex-display]f=h\circ g[/latex-display]Key Equation
| Composite function | [latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex] |
Key Concepts
- We can perform algebraic operations on functions.
- When functions are combined, the output of the first (inner) function becomes the input of the second (outer) function.
- The function produced by combining two functions is a composite function.
- The order of function composition must be considered when interpreting the meaning of composite functions.
- A composite function can be evaluated by evaluating the inner function using the given input value and then evaluating the outer function taking as its input the output of the inner function.
- A composite function can be evaluated from a table.
- A composite function can be evaluated from a graph.
- A composite function can be evaluated from a formula.
- The domain of a composite function consists of those inputs in the domain of the inner function that correspond to outputs of the inner function that are in the domain of the outer function.
- Just as functions can be combined to form a composite function, composite functions can be decomposed into simpler functions.
- Functions can often be decomposed in more than one way.
Glossary
- composite function
- the new function formed by function composition, when the output of one function is used as the input of another
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 111999. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 32907, 69936. Authored by: Smart, Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 5727. Authored by: Pepe, Mike. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 3674. Authored by: Rasmussen, Melonie, mb Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 3585. Authored by: Reidel, Jessica. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 16852. Authored by: Pierpoint, William. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 15772. Authored by: Master, Course. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 1600. Authored by: WebWork-Rochester, mb Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
