We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

学习指南 > College Algebra CoRequisite Course

Characteristics of Graphs of Logarithmic Functions

Learning Outcomes

  • Determine the domain and range of a logarithmic function.
  • Determine the x-intercept and vertical asymptote of a logarithmic function.
  • Identify whether a logarithmic function is increasing or decreasing and give the interval.
  • Identify the features of a logarithmic function that make it an inverse of an exponential function.
Before working with graphs, we will take a look at the domain (the set of input values) for which the logarithmic function is defined. Recall that the exponential function is defined as [latex]y={b}^{x}[/latex] for any real number x and constant [latex]b>0[/latex], [latex]b\ne 1[/latex], where
  • The domain of [latex]y[/latex] is [latex]\left(-\infty ,\infty \right)[/latex].
  • The range of [latex]y[/latex] is [latex]\left(0,\infty \right)[/latex].
In the last section we learned that the logarithmic function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] is the inverse of the exponential function [latex]y={b}^{x}[/latex]. So, as inverse functions:
  • The domain of [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] is the range of [latex]y={b}^{x}[/latex]: [latex]\left(0,\infty \right)[/latex].
  • The range of [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] is the domain of [latex]y={b}^{x}[/latex]: [latex]\left(-\infty ,\infty \right)[/latex].
Transformations of the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, stretches, compressions, and reflections—to the parent function without loss of shape. Previously we saw that certain transformations can change the range of [latex]y={b}^{x}[/latex]. Similarly, applying transformations to the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] can change the domain. Therefore, when finding the domain of a logarithmic function, it is important to remember that the domain consists only of positive real numbers. That is, the value you are applying the logarithmic function to, also known as the argument of the logarithmic function, must be greater than zero. For example, consider [latex]f\left(x\right)={\mathrm{log}}_{4}\left(2x - 3\right)[/latex]. This function is defined for any values of x such that the argument, in this case [latex]2x - 3[/latex], is greater than zero. To find the domain, we set up an inequality and solve for [latex]x[/latex]:

[latex]\begin{array}{l}2x - 3>0\hfill & \text{Show the argument greater than zero}.\hfill \\ 2x>3\hfill & \text{Add 3}.\hfill \\ x>\dfrac{3}{2}\hfill & \text{Divide by 2}.\hfill \end{array}[/latex]

In interval notation, the domain of [latex]f\left(x\right)={\mathrm{log}}_{4}\left(2x - 3\right)[/latex] is [latex]\left(\dfrac{3}{2},\infty \right)[/latex].

Tip for success

Finding the domain of the logarithm function is similar to finding the domain of the square root function. Recall that for [latex]y = \sqrt{u}, u\geq0[/latex], so the domain of [latex]y=\sqrt{2x-3}[/latex] is all [latex]x[/latex] for which [latex]2x-3\geq0[/latex], or all [latex]x\geq\dfrac{3}{2}[/latex]. Since the logarithm function takes input only strictly greater than zero, we see in the example above that the domain of [latex]f\left(x\right)={\mathrm{log}}_{4}\left(2x - 3\right)[/latex] is [latex]\left(\dfrac{3}{2},\infty \right)[/latex].

How To: Given a logarithmic function, identify the domain

  1. Set up an inequality showing the argument greater than zero.
  2. Solve for [latex]x[/latex].
  3. Write the domain in interval notation.

Example: Identifying the Domain Resulting From a Logarithmic Shift

What is the domain of [latex]f\left(x\right)={\mathrm{log}}_{2}\left(x+3\right)[/latex]?

Answer:

[latex]\begin{array}{l}x+3>0\hfill & \text{The argument must be positive}.\hfill \\ x>-3\hfill & \text{Subtract 3}.\hfill \end{array}[/latex]

  The logarithmic function is defined only when the argument is positive, so this function is defined when [latex]x+3>0[/latex]. The domain of [latex]f\left(x\right)={\mathrm{log}}_{2}\left(x+3\right)[/latex] is [latex]\left(-3,\infty \right)[/latex].

Try It

What is the domain of [latex]f\left(x\right)={\mathrm{log}}_{5}\left(x - 2\right)+1[/latex]?

Answer: [latex]\left(2,\infty \right)[/latex]

Example: Identifying the Domain Resulting From a Logarithmic Shift and Reflection

What is the domain of [latex]f\left(x\right)=\mathrm{log}\left(5 - 2x\right)[/latex]?

Answer: The logarithmic function is defined only when the argument is positive, so this function is defined when [latex]5 - 2x>0[/latex]. Solving this inequality,

[latex]\begin{array}{l}5 - 2x>0\hfill & \text{The argument must be positive}.\hfill \\ -2x>-5\hfill & \text{Subtract }5.\hfill \\ x<\frac{5}{2}\hfill & \text{Divide by }-2\text{ and switch the inequality}.\hfill \end{array}[/latex]

The domain of [latex]f\left(x\right)=\mathrm{log}\left(5 - 2x\right)[/latex] is [latex]\left(-\infty ,\frac{5}{2}\right)[/latex].

Try It

What is the domain of [latex]f\left(x\right)=\mathrm{log}\left(x - 5\right)+2[/latex]?

Answer: [latex]\left(5,\infty \right)[/latex]

[ohm_question]14399[/ohm_question]

Graphing a Logarithmic Function Using a Table of Values

Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] along with all of its transformations: shifts, stretches, compressions, and reflections. We begin with the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex]. Because every logarithmic function of this form is the inverse of an exponential function of the form [latex]y={b}^{x}[/latex], their graphs will be reflections of each other across the line [latex]y=x[/latex]. To illustrate this, we can observe the relationship between the input and output values of [latex]y={2}^{x}[/latex] and its equivalent logarithmic form [latex]x={\mathrm{log}}_{2}\left(y\right)[/latex] in the table below.

recall inverse relationships

Recall that if an invertible function [latex]f(x)[/latex] contains a point, [latex]\left(a, b\right)[/latex], then the inverse function [latex]f^{-1}\left(x\right)[/latex] must contain the point [latex]\left(b, a\right)[/latex].
x –3 –2 –1 0 1 2 3
[latex]{2}^{x}=y[/latex] [latex]\frac{1}{8}[/latex] [latex]\frac{1}{4}[/latex] [latex]\frac{1}{2}[/latex] 1 2 4 8
[latex]{\mathrm{log}}_{2}\left(y\right)=x[/latex] –3 –2 –1 0 1 2 3
Using the inputs and outputs from the table above, we can build another table to observe the relationship between points on the graphs of the inverse functions [latex]f\left(x\right)={2}^{x}[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].
[latex]f\left(x\right)={2}^{x}[/latex] [latex]\left(-3,\frac{1}{8}\right)[/latex] [latex]\left(-2,\frac{1}{4}\right)[/latex] [latex]\left(-1,\frac{1}{2}\right)[/latex] [latex]\left(0,1\right)[/latex] [latex]\left(1,2\right)[/latex] [latex]\left(2,4\right)[/latex] [latex]\left(3,8\right)[/latex]
[latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] [latex]\left(\frac{1}{8},-3\right)[/latex] [latex]\left(\frac{1}{4},-2\right)[/latex] [latex]\left(\frac{1}{2},-1\right)[/latex] [latex]\left(1,0\right)[/latex] [latex]\left(2,1\right)[/latex] [latex]\left(4,2\right)[/latex] [latex]\left(8,3\right)[/latex]
As we would expect, the x and y-coordinates are reversed for the inverse functions. The figure below shows the graphs of f and g.
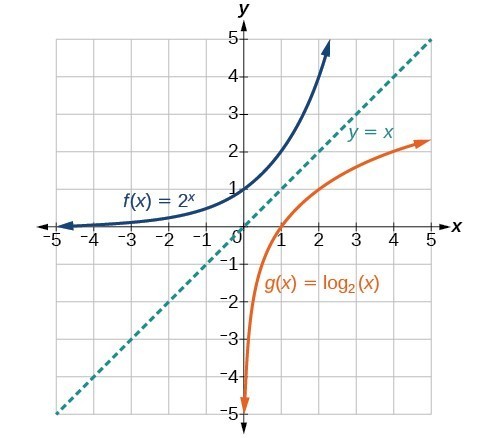Graph of two functions, f(x)=2^x and g(x)=log_2(x), with the line y=x denoting the axis of symmetry. Notice that the graphs of [latex]f\left(x\right)={2}^{x}[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] are reflections about the line y = x since they are inverses of each other.
Observe the following from the graph:
  • [latex]f\left(x\right)={2}^{x}[/latex] has a y-intercept at [latex]\left(0,1\right)[/latex] and [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] has an x-intercept at [latex]\left(1,0\right)[/latex].
  • The domain of [latex]f\left(x\right)={2}^{x}[/latex], [latex]\left(-\infty ,\infty \right)[/latex], is the same as the range of [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].
  • The range of [latex]f\left(x\right)={2}^{x}[/latex], [latex]\left(0,\infty \right)[/latex], is the same as the domain of [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex].

A General Note: Characteristics of the Graph of the Parent Function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]

For any real number x and constant b > 0, [latex]b\ne 1[/latex], we can see the following characteristics in the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]:
  • one-to-one function
  • vertical asymptote: x = 0
  • domain: [latex]\left(0,\infty \right)[/latex]
  • range: [latex]\left(-\infty ,\infty \right)[/latex]
  • x-intercept: [latex]\left(1,0\right)[/latex] and key point [latex]\left(b,1\right)[/latex]
  • y-intercept: none
  • increasing if [latex]b>1[/latex]
  • decreasing if 0 < b < 1

Try it

Use an online graphing tool to graph the function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] Adjust the [latex]b[/latex] value to investigate how changes in the base of the logarithmic function affect the graph of that function. Which function is an increasing function?  Which is decreasing? Does the x-intercept change when you change the base? Make sure to use values between [latex]0[/latex] and [latex]1[/latex] as well as values greater than [latex]1[/latex].
The graphs above show how changing the base b in [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] can affect the graphs. Observe that the graphs compress vertically as the value of the base increases. (Note: recall that the function [latex]\mathrm{ln}\left(x\right)[/latex] has base [latex]e\approx \text{2}.\text{718.)}[/latex]
Graph of three equations: y=log_2(x) in blue, y=ln(x) in orange, and y=log(x) in red. The y-axis is the asymptote. The graphs of three logarithmic functions with different bases all greater than 1.

How To: Given a logarithmic function Of the form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex], graph the function

  1. Draw and label the vertical asymptote, x = 0.
  2. Plot the x-intercept, [latex]\left(1,0\right)[/latex].
  3. Plot the key point [latex]\left(b,1\right)[/latex].
  4. Draw a smooth curve through the points.
  5. State the domain, [latex]\left(0,\infty \right)[/latex], the range, [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote, x = 0.

Example: Graphing a Logarithmic Function Of the Form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]

Graph [latex]f\left(x\right)={\mathrm{log}}_{5}\left(x\right)[/latex]. State the domain, range, and asymptote.

Answer: Before graphing, identify the behavior and key points for the graph.

  • Since b = 5 is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote x = 0, and the right tail will increase slowly without bound.
  • The x-intercept is [latex]\left(1,0\right)[/latex].
  • The key point [latex]\left(5,1\right)[/latex] is on the graph.
  • We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points.
Graph of f(x)=log_5(x) with labeled points at (1, 0) and (5, 1). The y-axis is the asymptote. The domain is [latex]\left(0,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = 0.

Try It

Graph [latex]f\left(x\right)={\mathrm{log}}_{\frac{1}{5}}\left(x\right)[/latex]. State the domain, range, and asymptote.

Answer: The domain is [latex]\left(0,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = 0. Graph of f(x)=log_(1/5)(x) with labeled points at (1/5, 1) and (1, 0). The y-axis is the asymptote.

[ohm_question]34999[/ohm_question] [ohm_question]35000[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Characteristics of Graphs of Logarithmic Functions Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/pajb6u9zzj. License: Public Domain: No Known Copyright.

CC licensed content, Shared previously

  • Questoin ID 34999, 35000. Authored by: Smart, JIm. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].