We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Direct Variation

Learning Outcomes

  • Solve a direct variation problem
  • Use a constant of variation to describe the relationship between two variables
A used-car company has just offered their best candidate, Nicole, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance if she sells a vehicle for $4,600, she will earn $736. She wants to evaluate the offer, but she is not sure how. In this section we will look at relationships, such as this one, between earnings, sales, and commission rate. In the example above, Nicole’s earnings can be found by multiplying her sales by her commission. The formula [latex]e = 0.16s[/latex] tells us her earnings, [latex]e[/latex], come from the product of 0.16, her commission, and the sale price of the vehicle, [latex]s[/latex]. If we create a table, we observe that as the sales price increases, the earnings increase as well, which should be intuitive.
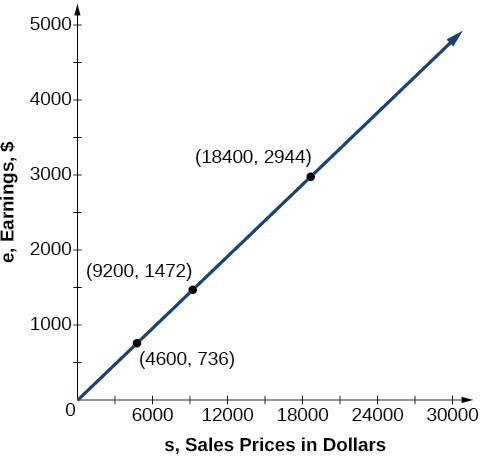
[latex]s[/latex], sales prices[latex]e = 0.16s[/latex]Interpretation
$4,600[latex]e=0.16(4,600)=736[/latex]A sale of a $4,600 vehicle results in $736 earnings.
$9,200[latex]e=0.16(9,200)=1,472[/latex]A sale of a $9,200 vehicle results in $1472 earnings.
$18,400[latex]e=0.16(18,400)=2,944[/latex]A sale of a $18,400 vehicle results in $2944 earnings.
Notice that earnings are a multiple of sales. As sales increase, earnings increase in a predictable way. Double the sales of the vehicle from $4,600 to $9,200, and we double the earnings from $736 to $1,472. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation. Each variable in this type of relationship varies directly with the other. The graph below represents the data for Nicole’s potential earnings. We say that earnings vary directly with the sales price of the car. The formula [latex]y=k{x}^{n}[/latex] is used for direct variation. The value [latex]k[/latex] is a nonzero constant greater than zero and is called the constant of variation. In this case, [latex]k=0.16[/latex] and [latex]n=1[/latex]. Graph of y=(0.16)x where the horizontal axis is labeled,

A General Note: Direct Variation

If [latex]x[/latex] and [latex]y[/latex] are related by an equation of the form

[latex]y=k{x}^{n}[/latex] then we say that the relationship is direct variation and [latex]y[/latex] varies directly with the [latex]n[/latex]th power of [latex]x[/latex]. In direct variation relationships, there is a nonzero constant ratio [latex]k=\dfrac{y}{{x}^{n}}[/latex], where [latex]k[/latex] is called the constant of variation, which help defines the relationship between the variables.

recall isolating a variable in a formula

We've learned to solve certain formulas for one of the variables. For example, in the formula that relates distance, rate, and time, [latex]d=rt[/latex], we can solve the equation for rate, [latex]r=\dfrac{d}{t}[/latex] or for time, [latex]t=\dfrac{d}{r}[/latex]. We say we are isolating the variable of interest in these cases. The same idea applies when solving a direct variation problem for the constant of variation, [latex]k[/latex]. Given a direct variation such as [latex]y=kx^n[/latex], we can isolate the constant of variation using the properties of equality to obtain [latex]\dfrac{y}{x^n}=k[/latex].

How To: Given a description of a direct variation problem, solve for an unknown.

  1. Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
  2. Determine the constant of variation. You may need to divide [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
  3. Use the constant of variation to write an equation for the relationship.
  4. Substitute known values into the equation to find the unknown.

Example: Solving a Direct Variation Problem

The quantity [latex]y[/latex] varies directly with the cube of [latex]x[/latex]. If [latex]y=25[/latex] when [latex]x=2[/latex], find [latex]y[/latex] when [latex]x[/latex] is 6.

Answer: The general formula for direct variation with a cube is [latex]y=k{x}^{3}[/latex]. The constant can be found by dividing [latex]y[/latex] by the cube of [latex]x[/latex].

[latex]\begin{align} k&=\dfrac{y}{{x}^{3}} \\[1mm] &=\dfrac{25}{{2}^{3}}\\[1mm] &=\dfrac{25}{8}\end{align}[/latex] Now use the constant to write an equation that represents this relationship.

[latex]y=\dfrac{25}{8}{x}^{3}[/latex] Substitute [latex]x=6[/latex] and solve for [latex]y[/latex].

[latex]\begin{align}y&=\dfrac{25}{8}{\left(6\right)}^{3} \\[1mm] &=675\hfill \end{align}[/latex]

Analysis of the Solution

The graph of this equation is a simple cubic, as shown below.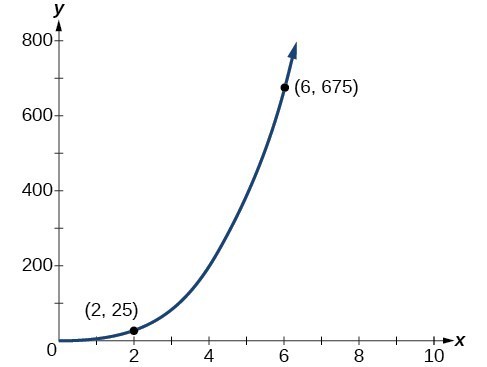   Graph of y=25/8(x^3) with the labeled points (2, 25) and (6, 675).

Q & A

Do the graphs of all direct variation equations look like the example above? No. Direct variation equations are power functions—they may be linear, quadratic, cubic, quartic, radical, etc. But all of the graphs pass through [latex](0, 0)[/latex].

Try It

The quantity [latex]y[/latex] varies directly with the square of [latex]y[/latex]. If [latex]y=24[/latex] when [latex]x=3[/latex], find [latex]y[/latex] when [latex]x[/latex] is 4.

Answer: [latex-display]\dfrac{128}{3}[/latex-display]

[embed]
Watch this video to see a quick lesson in direct variation.  You will see more worked examples. https://youtu.be/plFOq4JaEyI

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Question ID 91391. Authored by: Jenck, Michael. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Direct Variation Applications . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.