Write Domain and Range Given an Equation
Learning Outcomes
- Find the domain of a function defined by an equation.
- Write domain and range using standard notations.
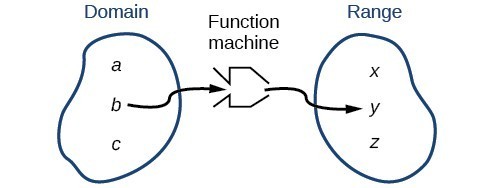 We can visualize the domain as a "holding area" that contains "raw materials" for a "function machine" and the range as another "holding area" for the machine’s products.
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and write [latex]\left(0,\text{ }100\right][/latex]. We will discuss interval notation in greater detail later.
Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.
Before we begin, let us review the conventions of interval notation:
We can visualize the domain as a "holding area" that contains "raw materials" for a "function machine" and the range as another "holding area" for the machine’s products.
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has $100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and write [latex]\left(0,\text{ }100\right][/latex]. We will discuss interval notation in greater detail later.
Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.
Before we begin, let us review the conventions of interval notation:
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- Parentheses, ( or ), are used to signify that an endpoint is not included, called exclusive.
- Brackets, [ or ], are used to indicate that an endpoint is included, called inclusive.
Example: Finding the Domain of a Function as a Set of Ordered Pairs
Find the domain of the following function: [latex]\left\{\left(2,\text{ }10\right),\left(3,\text{ }10\right),\left(4,\text{ }20\right),\left(5,\text{ }30\right),\left(6,\text{ }40\right)\right\}[/latex] .Answer: First identify the input values. The input value is the first coordinate in an ordered pair. There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.
[latex]\left\{2,3,4,5,6\right\}[/latex]
Try It
Find the domain of the function:[latex]\left\{\left(-5,4\right),\left(0,0\right),\left(5,-4\right),\left(10,-8\right),\left(15,-12\right)\right\}[/latex]
Answer: [latex-display]\left\{-5,0,5,10,15\right\}[/latex-display]
[ohm_question]7218[/ohm_question]How To: Given a function written in equation form, find the domain.
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Example: Finding the Domain of a Function
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].Answer: The input value, shown by the variable [latex]x[/latex] in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers. In interval form the domain of [latex]f[/latex] is [latex]\left(-\infty ,\infty \right)[/latex].
Try It
Find the domain of the function: [latex]f\left(x\right)=5-x+{x}^{3}[/latex].Answer: [latex-display]\left(-\infty ,\infty \right)[/latex-display]
[ohm_question]60533[/ohm_question]How To: Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . These are the values that cannot be inputs in the function.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example: Finding the Domain of a Function Involving a Denominator (Rational Function)
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].Answer: When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].
[latex]\begin{align}2-x&=0 \\ -x&=-2 \\ x&=2 \end{align}[/latex]
Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].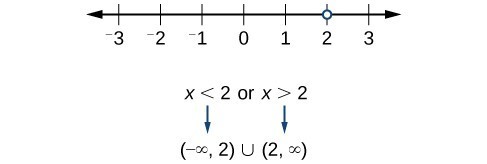 In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].
In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].
Try It
Find the domain of the function: [latex]f\left(x\right)=\dfrac{1+4x}{2x - 1}[/latex].Answer: [latex-display]\left(-\infty ,\frac{1}{2}\right)\cup \left(\frac{1}{2},\infty \right)[/latex-display]
[ohm_question]61836[/ohm_question]How To: Given a function written in equation form including an even root, find the domain.
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
division by zero and even roots of negative numbers
While zero divided by any number equals zero, division by zero results in an undefined ratio. [latex-display]\dfrac{0}{a} = 0 \quad \text{but } \quad \dfrac{b}{0} = und[/latex-display] An even root of a negative number does not exist in the real numbers. [latex-display]\sqrt{-1} = i[/latex-display] Since the domain of any function defined in the real plane is the set of all real input into the function, we must exclude any values of the input variable that create undefined expressions or even roots of a negative.Example: Finding the Domain of a Function with an Even Root
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].Answer: When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
[latex]\begin{align}7-x&\ge 0 \\ -x&\ge -7 \\ x&\le 7 \end{align}[/latex]
Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to [latex]7[/latex], or [latex]\left(-\infty ,7\right][/latex].Try It
Find the domain of the function [latex]f\left(x\right)=\sqrt{5+2x}[/latex].Answer: [latex]\left[-\frac{5}{2},\infty \right)[/latex]
[ohm_question]30831[/ohm_question] [ohm_question]92940[/ohm_question]Q & A
Can there be functions in which the domain and range do not intersect at all? Yes. For example, the function [latex]f\left(x\right)=-\frac{1}{\sqrt{x}}[/latex] has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.Try It
When you are defining the domain of a function, it can help to graph it, especially when you have a rational or a function with an even root. First, determine the domain restrictions for the following functions, then graph each one to check whether your domain agrees with the graph.- [latex]f(x) = \sqrt{2x-4}+5[/latex]
- [latex]g(x) = \dfrac{2x+4}{x-1}[/latex]
How To: Given the formula for a function, determine the domain and range.
- Exclude from the domain any input values that result in division by zero.
- Exclude from the domain any input values that have nonreal (or undefined) number outputs.
- Use the valid input values to determine the range of the output values.
- Look at the function graph and table values to confirm the actual function behavior.
Example: Finding the Domain and Range Using Toolkit Functions
Find the domain and range of [latex]f\left(x\right)=2{x}^{3}-x[/latex].Answer: There are no restrictions on the domain, as any real number may be cubed and then subtracted from the result. The domain is [latex]\left(-\infty ,\infty \right)[/latex] and the range is also [latex]\left(-\infty ,\infty \right)[/latex].
Example: Finding the Domain and Range
Find the domain and range of [latex]f\left(x\right)=\dfrac{2}{x+1}[/latex].Answer: We cannot evaluate the function at [latex]-1[/latex] because division by zero is undefined. The domain is [latex]\left(-\infty ,-1\right)\cup \left(-1,\infty \right)[/latex]. Because the function is never zero, we exclude 0 from the range. The range is [latex]\left(-\infty ,0\right)\cup \left(0,\infty \right)[/latex].
Example: Finding the Domain and Range
Find the domain and range of [latex]f\left(x\right)=2\sqrt{x+4}[/latex].Answer: We cannot take the square root of a negative number, so the value inside the radical must be nonnegative. [latex-display]x+4\ge 0\text{ when }x\ge -4[/latex-display] The domain of [latex]f\left(x\right)[/latex] is [latex]\left[-4,\infty \right)[/latex]. We then find the range. We know that [latex]f\left(-4\right)=0[/latex], and the function value increases as [latex]x[/latex] increases without any upper limit. We conclude that the range of [latex]f[/latex] is [latex]\left[0,\infty \right)[/latex].
Analysis of the Solution
The graph below represents the function [latex]f[/latex].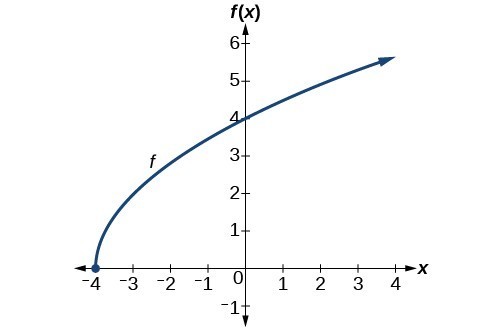
Try It
Find the domain and range of [latex]f\left(x\right)=-\sqrt{2-x}[/latex].Answer: Domain: [latex]\left(-\infty ,2\right][/latex] Range: [latex]\left(-\infty ,0\right][/latex]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 60533, 61836. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Finding Function Values. Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube License.
- Ex: Evaluate a Function and Solve for a Function Value Given a Table. Provided by: Phoenix College Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube LIcense.
- Ex1: Evaluate a Function and Solve for a Function Value Given a Graph. Provided by: Phoenix College Authored by: Mathispower4u. License: All Rights Reserved. License terms: Standard YouTube LIcense.
- Find Function Inputs for a Given Quadratic Function Output. Authored by: James Sousa. License: All Rights Reserved. License terms: Standard YouTube License.
- Write a Linear Relation as a Function. Authored by: James Sousa. License: All Rights Reserved. License terms: Standard YouTube License.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 72181. Authored by: Carmichael,Patrick. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 30831. Authored by: Smart, Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 92940. Authored by: Jenck, Michael. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
