Parabolas with Vertices at the Origin
Learning Outcomes
- Identify and label the focus, directrix, and endpoints of the focal diameter of a parabola.
- Write the equation of a parabola given a focus and directrix.
 Parabola
Parabolatip for success
You've seen parabolas before as the set of all points satisfying a quadratic function. We'll look at the geometric form of a parabola in this section. It still describes a set of points that satisfy an equation in two variables, but without the need to qualify as a function, it can open left and right as well as up and down. It will be necessary to use another form of its equation to take all of the characteristics of this object into consideration. You'll learn new terminology for the parts of a parabola just as you did with the ellipse and hyperbola as well.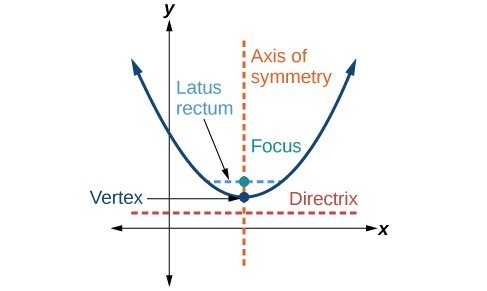 Key features of the parabola
Key features of the parabola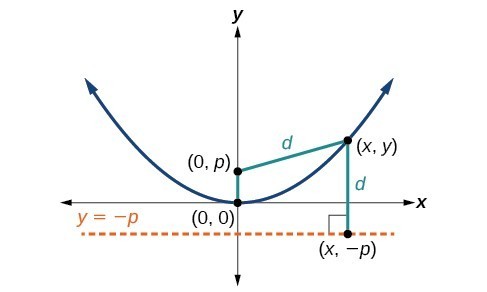 Let [latex]\left(x,y\right)[/latex] be a point on the parabola with vertex [latex]\left(0,0\right)[/latex], focus [latex]\left(0,p\right)[/latex], and directrix [latex]y= -p[/latex] as shown in Figure 4. The distance [latex]d[/latex] from point [latex]\left(x,y\right)[/latex] to point [latex]\left(x,-p\right)[/latex] on the directrix is the difference of the y-values: [latex]d=y+p[/latex]. The distance from the focus [latex]\left(0,p\right)[/latex] to the point [latex]\left(x,y\right)[/latex] is also equal to [latex]d[/latex] and can be expressed using the distance formula.
Let [latex]\left(x,y\right)[/latex] be a point on the parabola with vertex [latex]\left(0,0\right)[/latex], focus [latex]\left(0,p\right)[/latex], and directrix [latex]y= -p[/latex] as shown in Figure 4. The distance [latex]d[/latex] from point [latex]\left(x,y\right)[/latex] to point [latex]\left(x,-p\right)[/latex] on the directrix is the difference of the y-values: [latex]d=y+p[/latex]. The distance from the focus [latex]\left(0,p\right)[/latex] to the point [latex]\left(x,y\right)[/latex] is also equal to [latex]d[/latex] and can be expressed using the distance formula.
[latex]\begin{align}d&=\sqrt{{\left(x - 0\right)}^{2}+{\left(y-p\right)}^{2}} \\ &=\sqrt{{x}^{2}+{\left(y-p\right)}^{2}} \end{align}[/latex]
Set the two expressions for [latex]d[/latex] equal to each other and solve for [latex]y[/latex] to derive the equation of the parabola. We do this because the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(0,p\right)[/latex] equals the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(x, -p\right)[/latex].[latex]\sqrt{{x}^{2}+{\left(y-p\right)}^{2}}=y+p[/latex]
We then square both sides of the equation, expand the squared terms, and simplify by combining like terms.[latex]\begin{gathered}{x}^{2}+{\left(y-p\right)}^{2}={\left(y+p\right)}^{2} \\ {x}^{2}+{y}^{2}-2py+{p}^{2}={y}^{2}+2py+{p}^{2}\\ {x}^{2}-2py=2py \\ {x}^{2}=4py\end{gathered}[/latex]
The equations of parabolas with vertex [latex]\left(0,0\right)[/latex] are [latex]{y}^{2}=4px[/latex] when the x-axis is the axis of symmetry and [latex]{x}^{2}=4py[/latex] when the y-axis is the axis of symmetry. These standard forms are given below, along with their general graphs and key features.A General Note: Standard Forms of Parabolas with Vertex (0, 0)
The table below summarizes the standard features of parabolas with a vertex at the origin.| Axis of Symmetry | Equation | Focus | Directrix | Endpoints of Focal Diameter |
| x-axis | [latex]{y}^{2}=4px[/latex] | [latex]\left(p,\text{ }0\right)[/latex] | [latex]x=-p[/latex] | [latex]\left(p,\text{ }\pm 2p\right)[/latex] |
| y-axis | [latex]{x}^{2}=4py[/latex] | [latex]\left(0,\text{ }p\right)[/latex] | [latex]y=-p[/latex] | [latex]\left(\pm 2p,\text{ }p\right)[/latex] |
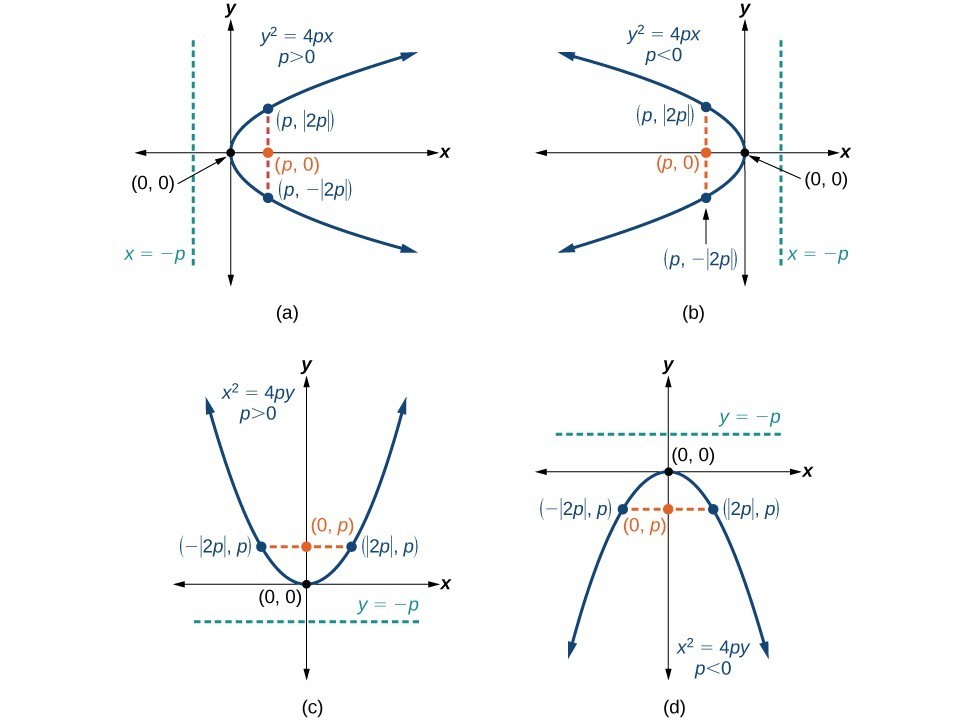 (a) When [latex]p>0[/latex] and the axis of symmetry is the x-axis, the parabola opens right. (b) When [latex]p<0[/latex] and the axis of symmetry is the x-axis, the parabola opens left. (c) When [latex]p<0[/latex] and the axis of symmetry is the y-axis, the parabola opens up. (d) When [latex]\text{ }p<0\text{ }[/latex] and the axis of symmetry is the y-axis, the parabola opens down.
(a) When [latex]p>0[/latex] and the axis of symmetry is the x-axis, the parabola opens right. (b) When [latex]p<0[/latex] and the axis of symmetry is the x-axis, the parabola opens left. (c) When [latex]p<0[/latex] and the axis of symmetry is the y-axis, the parabola opens up. (d) When [latex]\text{ }p<0\text{ }[/latex] and the axis of symmetry is the y-axis, the parabola opens down.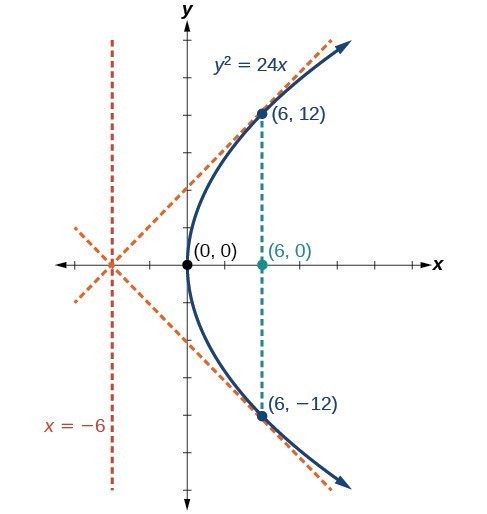
How To: Given a standard form equation for a parabola centered at (0, 0), sketch the graph.
- Determine which of the standard forms applies to the given equation: [latex]{y}^{2}=4px[/latex] or [latex]{x}^{2}=4py[/latex].
- Use the standard form identified in Step 1 to determine the axis of symmetry, focus, equation of the directrix, and endpoints of the focal diameter.
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- the axis of symmetry is the x-axis, [latex]y=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of x in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p<0[/latex], the parabola opens left.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(p,0\right)[/latex]
- use [latex]p[/latex] to find the equation of the directrix, [latex]x=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(p,\pm 2p\right)[/latex]. Alternately, substitute [latex]x=p[/latex] into the original equation.
- If the equation is in the form [latex]{x}^{2}=4py[/latex], then
- the axis of symmetry is the y-axis, [latex]x=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of y in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens up. If [latex]p<0[/latex], the parabola opens down.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(0,p\right)[/latex]
- use [latex]p[/latex] to find equation of the directrix, [latex]y=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(\pm 2p,p\right)[/latex]
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- Plot the focus, directrix, and focal diameter, and draw a smooth curve to form the parabola.
Example: Graphing a Parabola with Vertex (0, 0) and the x-axis as the Axis of Symmetry
Graph [latex]{y}^{2}=24x[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer: The standard form that applies to the given equation is [latex]{y}^{2}=4px[/latex]. Thus, the axis of symmetry is the x-axis. It follows that:
- [latex]24=4p[/latex], so [latex]p=6[/latex]. Since [latex]p>0[/latex], the parabola opens right the coordinates of the focus are [latex]\left(p,0\right)=\left(6,0\right)[/latex]
- the equation of the directrix is [latex]x=-p=-6[/latex]
- the endpoints of the focal diameter have the same x-coordinate at the focus. To find the endpoints, substitute [latex]x=6[/latex] into the original equation: [latex]\left(6,\pm 12\right)[/latex]
Try It
Graph [latex]{y}^{2}=-16x[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer:
Focus: [latex]\left(-4,0\right)[/latex]; Directrix: [latex]x=4[/latex]; Endpoints of the latus rectum: [latex]\left(-4,\pm 8\right)[/latex]

Example: Graphing a Parabola with Vertex (0, 0) and the y-axis as the Axis of Symmetry
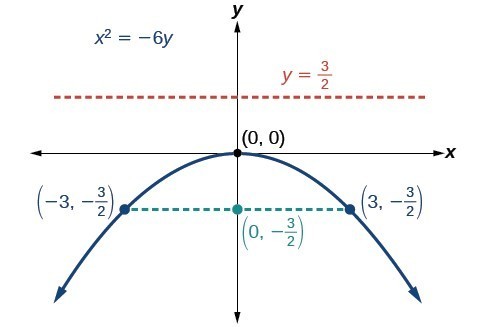
Graph [latex]{x}^{2}=-6y[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer: The standard form that applies to the given equation is [latex]{x}^{2}=4py[/latex]. Thus, the axis of symmetry is the y-axis. It follows that:
- [latex]-6=4p[/latex], so [latex]p=-\frac{3}{2}[/latex]. Since [latex]p<0[/latex], the parabola opens down.
- the coordinates of the focus are [latex]\left(0,p\right)=\left(0,-\frac{3}{2}\right)[/latex]
- the equation of the directrix is [latex]y=-p=\frac{3}{2}[/latex]
- the endpoints of the focal diameter can be found by substituting [latex]\text{ }y=\frac{3}{2}\text{ }[/latex] into the original equation, [latex]\left(\pm 3,-\frac{3}{2}\right)[/latex]
Try It
Graph [latex]{x}^{2}=8y[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer:
Focus: [latex]\left(0,2\right)[/latex]; Directrix: [latex]y=-2[/latex]; Endpoints of the latus rectum: [latex]\left(\pm 4,2\right)[/latex].
Try It
Use an online graphing tool to plot the following parabola whose axis of symmetry is the x-axis, [latex]y^2=4px[/latex] Adjust the free variable [latex]p[/latex] to values between [latex]-10,10[/latex]. Your task in this exercise is to add the focus, directrix, and endpoints of the focal diameter in terms of the free variable, [latex]p[/latex]. For example, to add the focus, you would define a point, [latex](p,0)[/latex] .Answer:

Writing Equations of Parabolas in Standard Form
In the previous examples we used the standard form equation of a parabola to calculate the locations of its key features. We can also use the calculations in reverse to write an equation for a parabola when given its key features.tip for success
In this section, we will write the equation of a parabola in standard form, as opposed to the equation of a quadratic or second degree polynomial. The language we use when discussing the object is specific. It is true that a quadratic function forms a parabola when graphed in the plane, but here we are using the phrase standard form of the equation of a parabola to indicate that we wish to describe the geometric object. When talking about this object in this context, we would naturally use the equations described below.How To: Given its focus and directrix, write the equation for a parabola in standard form.
- Determine whether the axis of symmetry is the x- or y-axis.
- If the given coordinates of the focus have the form [latex]\left(p,0\right)[/latex], then the axis of symmetry is the x-axis. Use the standard form [latex]{y}^{2}=4px[/latex].
- If the given coordinates of the focus have the form [latex]\left(0,p\right)[/latex], then the axis of symmetry is the y-axis. Use the standard form [latex]{x}^{2}=4py[/latex].
- Multiply [latex]4p[/latex].
- Substitute the value from Step 2 into the equation determined in Step 1.
Example: Writing the Equation of a Parabola in Standard Form Given its Focus and Directrix
What is the equation for the parabola with focus [latex]\left(-\frac{1}{2},0\right)[/latex] and directrix [latex]x=\frac{1}{2}?[/latex]Answer: The focus has the form [latex]\left(p,0\right)[/latex], so the equation will have the form [latex]{y}^{2}=4px[/latex]. Multiplying [latex]4p[/latex], we have [latex]4p=4\left(-\frac{1}{2}\right)=-2[/latex]. Substituting for [latex]4p[/latex], we have [latex]{y}^{2}=4px=-2x[/latex]. Therefore, the equation for the parabola is [latex]{y}^{2}=-2x[/latex].
Try It
What is the equation for the parabola with focus [latex]\left(0,\frac{7}{2}\right)[/latex] and directrix [latex]y=-\frac{7}{2}[/latex]?Answer: [latex-display]{x}^{2}=14y[/latex-display]
[embed]Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Graphing Parabolas Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/wunbnybenw. License: Public Domain: No Known Copyright.
- Graphing Parabolas - With Solutions Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/b3buagwzwl. License: Public Domain: No Known Copyright.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 23511. Authored by: Shahbazian,Roy, mb McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 23711. Authored by: McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
