Learning Outcomes
By the end of this lesson, you will be able to:
- Use slope-intercept form to plot and write equations of lines.
- Use point-slope form to write the equation of a line.
- Write the equation of a line in standard form.
- Recognize vertical and horizontal lines from their graphs and equations.
- Determine whether two lines are parallel or perpendicular.
- Find the equations of parallel and perpendicular lines.
- Write the equations of lines that are parallel or perpendicular to a given line.
Now that we have learned how to plot points on a coordinate plane and graph linear equations, we can begin to analyze the equations of lines and evaluate the different characteristics of these lines. In this section, we will learn about the commonly used forms for writing linear equations and the properties of lines that can be determined from their equations.
For example, without creating a table of values, you will be able to match each equation below to its corresponding graph. You will also be able to explain the similarities and differences of each line, how they relate to each other, and why they behave that way.
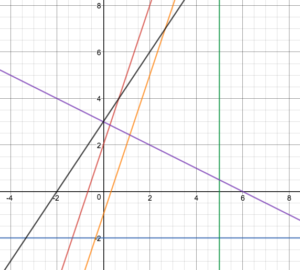(a) [latex]y=3x+2[/latex]
(b) [latex]y-4=-\frac{1}{2}(x+2)[/latex]
(c) [latex]x=5[/latex]
(d) [latex]y=-2[/latex]
(e) [latex]3x=y+1[/latex]
(f) [latex]2y-3x=6[/latex]