We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Polynomial Long Division

Learning Outcomes

  • Use long division to divide polynomials.
In the next two sections, we will be learning two ways to divide polynomials. These techniques can help you find the zeros of a polynomial that is not factorable over the integers.

recall long division

A handy algebraic technique involves rewriting a quotient of polynomials as a polynomial of reduced degree plus a remainder quotient

[latex]\dfrac{p(x)}{q(x)}=h(x)+\dfrac{r(x)}{q(x)}[/latex].

Or equivalently by multiplying both sides by [latex]q(x)[/latex],

[latex]p(x)=q(x)h(x) + r(x)[/latex]

This method is akin to rewriting an "improper" fraction such as

[latex]\dfrac{17}{3} = 5 + \dfrac{2}{3}[/latex].

Or equivalently,

[latex]17=3\cdot 5 + 2[/latex].

The process used to accomplish this is similar to long division of whole numbers, so if you haven't performed long division for awhile, take a moment to refresh before reading this section.

Answer: Recall how you can use long division to divide two whole numbers, say [latex]900[/latex] divided by [latex]37[/latex]. The dividend in 900 and the divisor is 37. First, you would think about how many [latex]37s[/latex] are in [latex]90[/latex], as [latex]9[/latex] is too small. (Note: you could also think, how many [latex]40s[/latex] are there in [latex]90[/latex].) There are two [latex]37s[/latex] in [latex]90[/latex], so write [latex]2[/latex] above the last digit of [latex]90[/latex]. Two [latex]37s[/latex] is [latex]74[/latex]; write that product below the [latex]90[/latex]. 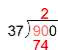Screen Shot 2016-03-28 at 3.35.17 PM Subtract: [latex]90–74[/latex] is [latex]16[/latex]. (If the result is larger than the divisor, [latex]37[/latex], then you need to use a larger number for the quotient.) 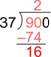Bring down the next digit [latex](0)[/latex] and consider how many 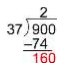[latex]37s[/latex] are in [latex]160[/latex]. Screen Shot 2016-03-28 at 3.36.06 PM There are four [latex]37s[/latex] in [latex]160[/latex], so write the [latex]4[/latex] next to the two in the quotient. Four [latex]37s[/latex] is [latex]148[/latex]; write that product below the 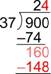[latex]160[/latex]. Subtract: [latex]160–148[/latex] is [latex]12[/latex]. This is less than [latex]37[/latex] so the [latex]4[/latex] is correct. Since there are no more digits in the dividend to bring down, you are done. 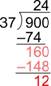The final answer is [latex]24[/latex] R[latex]12[/latex], or [latex]24\frac{12}{37}[/latex]. You can check this by multiplying the quotient (without the remainder) by the divisor, and then adding in the remainder. The result should be the dividend:

[latex]24\cdot37+12=888+12=900[/latex]

======================================================================================= We are familiar with the long division algorithm for ordinary arithmetic. We begin by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat. For example, let’s divide 178 by 3 using long division. Long Division. Step 1, 5 times 3 equals 15 and 17 minus 15 equals 2. Step 2: Bring down the 8. Step 3: 9 times 3 equals 27 and 28 minus 27 equals 1. Answer: 59 with a remainder of 1 or 59 and one-third. Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.

[latex]\begin{array}{l}\left(\text{divisor }\cdot \text{ quotient}\right)\text{ + remainder}\text{ = dividend}\hfill \\ \left(3\cdot 59\right)+1 = 177+1 = 178\hfill \end{array}[/latex]

We call this the Division Algorithm and will discuss it more formally after looking at an example. Division of polynomials that contain more than one term has similarities to long division of whole numbers. We can write a polynomial dividend as the product of the divisor and the quotient added to the remainder. The terms of the polynomial division correspond to the digits (and place values) of the whole number division. This method allows us to divide two polynomials. For example, if we were to divide [latex]2{x}^{3}-3{x}^{2}+4x+5[/latex] by [latex]x+2[/latex] using the long division algorithm, it would look like this: Set up the division problem. 2x cubed divided by x is 2x squared. Multiply the sum of x and 2 by 2x squared. Subtract. Then bring down the next term. Negative 7x squared divided by x is negative 7x. Multiply the sum of x and 2 by negative 7x. Subtract, then bring down the next term. 18x divided by x is 18. Multiply the sum of x and 2 by 18. Subtract. We have found

[latex]\frac{2{x}^{3}-3{x}^{2}+4x+5}{x+2}=2{x}^{2}-7x+18-\frac{31}{x+2}[/latex]

or

[latex]2{x}^{3}-3{x}^{2}+4x+5=\left(x+2\right)\left(2{x}^{2}-7x+18\right)-31[/latex]

We can identify the dividend, divisor, quotient, and remainder. 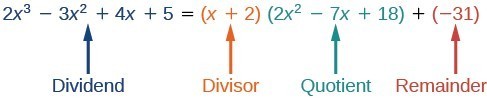The dividend is 2x cubed minus 3x squared plus 4x plus 5. The divisor is x plus 2. The quotient is 2x squared minus 7x plus 18. The remainder is negative 31. Writing the result in this manner illustrates the Division Algorithm.

A General Note: The Division Algorithm

The Division Algorithm states that given a polynomial dividend [latex]f\left(x\right)[/latex] and a non-zero polynomial divisor [latex]d\left(x\right)[/latex] where the degree of [latex]d\left(x\right)[/latex] is less than or equal to the degree of [latex]f\left(x\right)[/latex], there exist unique polynomials [latex]q\left(x\right)[/latex] and [latex]r\left(x\right)[/latex] such that

[latex]f\left(x\right)=d\left(x\right)q\left(x\right)+r\left(x\right)[/latex]

[latex]q\left(x\right)[/latex] is the quotient and [latex]r\left(x\right)[/latex] is the remainder. The remainder is either equal to zero or has degree strictly less than [latex]d\left(x\right)[/latex]. If [latex]r\left(x\right)=0[/latex], then [latex]d\left(x\right)[/latex] divides evenly into [latex]f\left(x\right)[/latex]. This means that both [latex]d\left(x\right)[/latex] and [latex]q\left(x\right)[/latex] are factors of [latex]f\left(x\right)[/latex].

How To: Given a polynomial and a binomial, use long division to divide the polynomial by the binomial

  1. Set up the division problem.
  2. Determine the first term of the quotient by dividing the leading term of the dividend by the leading term of the divisor.
  3. Multiply the answer by the divisor and write it below the like terms of the dividend.
  4. Subtract the bottom binomial from the terms above it.
  5. Bring down the next term of the dividend.
  6. Repeat steps 2–5 until reaching the last term of the dividend.
  7. If the remainder is non-zero, express as a fraction using the divisor as the denominator.

Example: Using Long Division to Divide a Second-Degree Polynomial

Divide [latex]5{x}^{2}+3x - 2[/latex] by [latex]x+1[/latex].

Answer: Set up the division problem. 5x squared divided by x is 5x. Multiply x plus 1 by 5x. Subtract. Bring down the next term. Negative 2x divded by x is negative 2. Multiply x + 1 by negative 2. Subtract.The quotient is [latex]5x - 2[/latex]. The remainder is 0. We write the result as

[latex]\frac{5{x}^{2}+3x - 2}{x+1}=5x - 2[/latex]

or

[latex]5{x}^{2}+3x - 2=\left(x+1\right)\left(5x - 2\right)[/latex]

Analysis of the Solution

This division problem had a remainder of 0. This tells us that the dividend is divided evenly by the divisor and that the divisor is a factor of the dividend.

Example: Using Long Division to Divide a Third-Degree Polynomial

Divide [latex]6{x}^{3}+11{x}^{2}-31x+15[/latex] by [latex]3x - 2[/latex].

Answer: 6x cubed divided by 3x is 2x squared. Multiply the sum of x and 2 by 2x squared. Subtract. Bring down the next term. 15x squared divided by 3x is 5x. Multiply 3x minus 2 by 5x. Subtract. Bring down the next term. Negative 21x divided by 3x is negative 7. Multiply 3x minus 2 by negative 7. Subtract. The remainder is 1. There is a remainder of 1. We can express the result as: [latex-display]\frac{6{x}^{3}+11{x}^{2}-31x+15}{3x - 2}=2{x}^{2}+5x - 7+\frac{1}{3x - 2}[/latex-display]

Analysis of the Solution

We can check our work by using the Division Algorithm to rewrite the solution then multiplying. [latex-display]\left(3x - 2\right)\left(2{x}^{2}+5x - 7\right)+1=6{x}^{3}+11{x}^{2}-31x+15[/latex-display] Notice, as we write our result,
  • the dividend is [latex]6{x}^{3}+11{x}^{2}-31x+15[/latex]
  • the divisor is [latex]3x - 2[/latex]
  • the quotient is [latex]2{x}^{2}+5x - 7[/latex]
  • the remainder is 1

Try It

Divide [latex]16{x}^{3}-12{x}^{2}+20x - 3[/latex] by [latex]4x+5[/latex].

Answer: [latex]4{x}^{2}-8x+15-\frac{78}{4x+5}[/latex]

[ohm_question]29482[/ohm_question]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Question ID 29482. Authored by: McClure,Caren. License: Other. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program.. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.