We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Projectile Motion

Learning Outcomes

  • Define projectile motion
  • Solve a polynomial function that represents projectile motion
  • Interpret the solution to a polynomial function that represents projectile motion
Projectile motion happens when you throw a ball into the air and it comes back down because of gravity.  A projectile will follow a curved path that behaves in a predictable way.  This predictable motion has been studied for centuries, and in simple cases, an object's height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where [latex]h(t)[/latex] represents the height of an object at a given time, [latex]t[/latex].  Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile's motion, as in the water in the image of the fountain below.
Water from a fountain shoing classic parabolic motion. Parabolic water trajectory in a fountain.
Parabolic motion and its related functions allow us to launch satellites for telecommunications and rockets for space exploration. Recently, police departments have even begun using projectiles with GPS to track fleeing suspects in vehicles rather than pursuing them by high-speed chase [footnote]"Cops' Latest Tool in High-speed Chases: GPS Projectiles." CBSNews. CBS Interactive, n.d. Web. [latex]14[/latex] June [latex]2016[/latex].[/footnote]. In this section, we will use polynomial functions to answer questions about the parabolic motion of a projectile. The real mathematical model for the path of a rocket or a police GPS projectile may have different coefficients or more variables, but the concept remains the same. We will also learn to interpret the meaning of the variables in a polynomial function that models projectile motion.

Example

A small toy rocket is launched from a [latex]4[/latex]-foot pedestal. The height (h, in feet) of the rocket t seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?

Answer: The rocket will be on the ground when [latex]h(t)=0[/latex]. We want to know how long, [latex]t[/latex], the rocket is in the air. [latex-display]\begin{array}{l}h(t)=−2t^{2}+7t+4=0\\0=−2t^{2}+7t+4\end{array}[/latex-display] We can factor the polynomial [latex]−2t^{2}+7t+4[/latex] more easily by first factoring out a [latex]-1[/latex] [latex-display]\begin{array}{c}0=-1(2t^{2}-7t-4)\\0=-1\left(2t+1\right)\left(t-4\right)\end{array}[/latex-display] Use the Zero Product Property. There is no need to set the constant factor [latex]-1[/latex] to zero, because [latex]-1[/latex] will never equal zero.

[latex]2t+1=0\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,t-4=0[/latex]

Solve each equation.

[latex]t=-\frac{1}{2}\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,t=4[/latex]

Interpret the answer. Since t represents time, it cannot be a negative number; only [latex]t=4[/latex] makes sense in this context. We can check our answer when [latex]t=4[/latex]. [latex-display]\begin{array}{c}h(4)=−2(4)^{2}+7(4)+4=0\\h(4)=-2(16)+28+4=0\\h(4)-32+32=0\\h(4)=0\end{array}[/latex-display] Therefore, the rocket will hit the ground 4 seconds after being launched.

In the next example, we will solve for the time that the rocket reaches a given height other than zero.

Example

Use the formula for the height of the rocket in the previous example to find the time when the rocket is [latex]4[/latex] feet from hitting the ground on its way back down.  Refer to the image. [latex-display]h(t)=−2t^{2}+7t+4[/latex-display]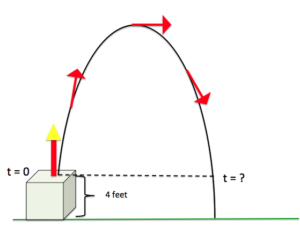 Parabolic motion of rocket which starts four feet up from the ground. t=0 is labeled at the starti of hte parabolic motion adn t=? is labeled at four feet from the ground on the other side of the parabola.

Answer: We are given that the height of the rocket is [latex]4[/latex] feet from the ground on its way back down. We want to know how long it will take for the rocket to get to that point in its path. We are going to solve for t. Substitute [latex]h(t) = 4[/latex] into the formula for height, and try to get zero on one side since we know we can use the zero product principle to solve polynomials. Write and Solve:

[latex]\begin{array}{l}h(t)=4=−2t^{2}+7t+4\\4=-2t^2+7t+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\0=-2t^2+7t\end{array}[/latex]

Now we can factor out a [latex]t[/latex] from each term:

[latex]0=t\left(-2t+7\right)[/latex]

Solve each equation for [latex]t[/latex] using the zero product principle:

[latex]\begin{array}{l}t=0\text{ OR }-2t+7=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-7}\,\,\,\,\,\,\,\underline{-7}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-2t}{-2}=\frac{-7}{-2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=\frac{7}{2}=3.5\end{array}[/latex]

It does not make sense for us to choose [latex]t=0[/latex], because we are interested in the amount of time that has passed when the projectile is [latex]4[/latex] feet from hitting the ground on its way back down. We will choose [latex]t=3.5[/latex].

Check the answer on your own for practice.

The rocket will be 4 feet from the ground at [latex]t=3.5\text{ seconds}[/latex].

In the following video, we show another example of how to find the time when a object following a parabolic trajectory hits the ground. https://youtu.be/hsWSzu3KcPU

Licenses & Attributions

CC licensed content, Original

  • Parabolic motion description and example. Provided by: Lumen Learning License: CC BY: Attribution.
  • Factoring Application - Find the Time When a Projectile Hits and Ground. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously