Sequences Defined by a Recursive Formula

[latex]\begin{align}{a}_{1}&=3 \\ {a}_{n}&=2{a}_{n - 1}-1, \text{for } n\ge 2 \end{align}[/latex] We can find the subsequent terms of the sequence using the first term.

[latex]\begin{align}{a}_{1}&=3\\ {a}_{2}&=2{a}_{1}-1=2\left(3\right)-1=5\\ {a}_{3}&=2{a}_{2}-1=2\left(5\right)-1=9\\ {a}_{4}&=2{a}_{3}-1=2\left(9\right)-1=17\end{align}[/latex] So the first four terms of the sequence are [latex]\left\{3,5,9,17\right\}[/latex]. The recursive formula for the Fibonacci sequence states the first two terms and defines each successive term as the sum of the preceding two terms.

[latex]\begin{align}{a}_{1}&=1 \\ {a}_{2}&=1 \\ {a}_{n}&={a}_{n - 1}+{a}_{n - 2}, \text{for } n\ge 3 \end{align}[/latex] To find the tenth term of the sequence, for example, we would need to add the eighth and ninth terms. We saw above that the eighth and ninth terms are 21 and 34, so

[latex]{a}_{10}={a}_{9}+{a}_{8}=34+21=55[/latex]

Using Factorial Notation

EXAMPLE: WRITING THE TERMS OF A SEQUENCE USING FACTORIALS

Write the first five terms of the sequence defined by the explicit formula [latex]{a}_{n}=\dfrac{5n}{\left(n+2\right)!}[/latex].

Answer: Substitute [latex]n=1,n=2[/latex], and so on in the formula.

[latex]\begin{align}&n=1 && {a}_{1}=\dfrac{5\left(1\right)}{\left(1+2\right)!}=\dfrac{5}{3!}=\dfrac{5}{3\cdot 2\cdot 1}=\dfrac{5}{6} \\[1mm] &n=2 && {a}_{2}=\dfrac{5\left(2\right)}{\left(2+2\right)!}=\dfrac{10}{4!}=\dfrac{10}{4\cdot 3\cdot 2\cdot 1}=\dfrac{5}{12} \\[1mm] &n=3 && {a}_{3}=\dfrac{5\left(3\right)}{\left(3+2\right)!}=\dfrac{15}{5!}=\dfrac{15}{5\cdot 4\cdot 3\cdot 2\cdot 1}=\dfrac{1}{8} \\[1mm] &n=4 && {a}_{4}=\dfrac{5\left(4\right)}{\left(4+2\right)!}=\dfrac{20}{6!}=\dfrac{20}{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=\dfrac{1}{36} \\[1mm] &n=5 && {a}_{5}=\dfrac{5\left(5\right)}{\left(5+2\right)!}=\dfrac{25}{7!}=\dfrac{25}{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=\dfrac{5}{1\text{,}008}\\ \text{ } \end{align}[/latex]

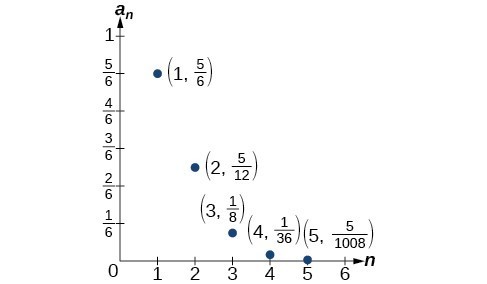
The first five terms are [latex]\left\{\dfrac{5}{6},\dfrac{5}{12},\dfrac{1}{8},\dfrac{1}{36},\dfrac{5}{1,008}\right\}[/latex]. Analysis of the Solution The figure below shows the graph of the sequence. Notice that, since factorials grow very quickly, the presence of the factorial term in the denominator results in the denominator becoming much larger than the numerator as [latex]n[/latex] increases. This means the quotient gets smaller and, as the plot of the terms shows, the terms are decreasing and nearing zero.

Licenses & Attributions