Why It Matters: Quadratic Functions
Why study quadratic functions?
An arrow is shot into the air. How high will it go? How far away will it land? It turns out that you can answer these and related questions with just a little knowledge of quadratic functions. In fact quadratic functions can be used to track to the position of any object that has been thrown, shot, or launched near the surface of the Earth. As long as wind resistance does not play a huge role and the distances are not too great, you can use a quadratic function to model the flight path.
For example, suppose an archer fires an arrow from a height of 2 meters above sea level on a calm day. While the arrow is in the air, someone else tracks and records its height precisely at each second. The following table shows the arrow’s height (meters) versus time (seconds).
| Time ([latex]t[/latex]) | Height ([latex]h[/latex]) |
| 0 sec. | 2 m |
| 1 sec. | 16.7m |
| 2 sec. | 21.6 m |
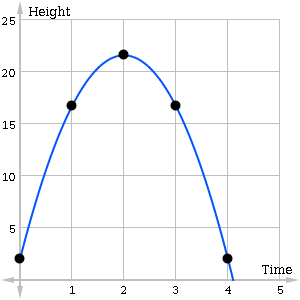Notice the up-and-down shape? As Isaac Newton would say, what goes up must come down. The smooth arc, first rising and then falling, is a tell-tale clue that there is a quadratic function lurking in the data. The curve that best fits this situation is a parabola, which is what we call the graph of a quadratic function. With a little more work, you can find the equation of this function:
[latex]h(t)=-4.9t^2+19.6t+2[/latex]
In the above equation, [latex]t[/latex] represents time in seconds, and [latex]h[/latex] represents height in meters. This is an example of a quadratic function. By analyzing the function, you can figure out precisely how high the arrow will go and when it will hit the ground. In this module you’ll learn how to graph and analyze quadratic functions and discover many other useful applications in which they play a role.Learning Outcomes
Complex Numbers- Express square roots of negative numbers as multiples of [latex]i[/latex].
- Plot complex numbers on the complex plane.
- Add and subtract complex numbers.
- Multiply and divide complex numbers.
Graphs of Quadratic Functions
- Recognize characteristics of parabolas.
- Understand how the graph of a parabola is related to its quadratic function.
Analysis of Quadratic Functions
- Use the quadratic formula and factoring to find both real and complex roots ([latex]x[/latex]-intercepts) of quadratic functions.
- Use algebra to find the [latex]y[/latex]-intercepts of a quadratic function.
- Solve problems involving the roots and intercepts of a quadratic function.
- Use the discriminant to determine the nature (real or complex) and quantity of solutions to quadratic equations.
- Determine a quadratic function’s minimum or maximum value.
- Solve problems involving a quadratic function’s minimum or maximum value.
Licenses & Attributions
CC licensed content, Original
- Why It Matters: Quadratic Functions. Authored by: Lumen Learning. License: CC BY: Attribution.
- Graph of parabolic motion. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Woman Holding Bow and Arrow. License: Public Domain: No Known Copyright.
