Converting Fractions to Decimals
Learning Outcomes
- Convert a fraction to a decimal
- Identify a fraction whose decimal form is repeating
- Add a fraction and decimal by converting between forms
Convert a Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.example
Write the fraction [latex]{\Large\frac{3}{4}}[/latex] as a decimal. Solution| A fraction bar means division, so we can write the fraction [latex]\Large\frac{3}{4}[/latex] using division. |  |
| Divide. |  |
| So the fraction [latex]{\Large\frac{3}{4}}[/latex] is equal to [latex]0.75[/latex]. |
try it
[ohm_question]146253[/ohm_question]example
Write the fraction [latex]-{\Large\frac{7}{2}}[/latex] as a decimal.Answer: Solution
| The value of this fraction is negative. After dividing, the value of the decimal will be negative. We do the division ignoring the sign, and then write the negative sign in the answer. | [latex]-{\Large\frac{7}{2}}[/latex] |
| Divide [latex]7[/latex] by [latex]2[/latex]. |  |
| So, | [latex]-{\Large\frac{7}{2}}=-3.5[/latex]. |
try it
[ohm_question]146257[/ohm_question]Repeating Decimals
So far, in all the examples converting fractions to decimals the division resulted in a remainder of zero. This is not always the case. Let’s see what happens when we convert the fraction [latex]{\Large\frac{4}{3}}[/latex] to a decimal. First, notice that [latex]{\Large\frac{4}{3}}[/latex] is an improper fraction. Its value is greater than [latex]1[/latex]. The equivalent decimal will also be greater than [latex]1[/latex].We divide [latex]4[/latex] by [latex]3[/latex].
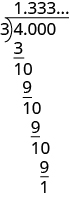 No matter how many more zeros we write, there will always be a remainder of [latex]1[/latex], and the threes in the quotient will go on forever. The number [latex]\text{1.333}\dots [/latex] is called a repeating decimal. Remember that the "…" means that the pattern repeats.
No matter how many more zeros we write, there will always be a remainder of [latex]1[/latex], and the threes in the quotient will go on forever. The number [latex]\text{1.333}\dots [/latex] is called a repeating decimal. Remember that the "…" means that the pattern repeats.
Repeating Decimal
A repeating decimal is a decimal in which the last digit or group of digits repeats endlessly.| [latex]\text{1.333}\ldots=1.\overline{3}[/latex] | [latex]3[/latex] is the repeating digit |
| [latex]\text{4.1666}\ldots=4.1\overline{6}[/latex] | [latex]6[/latex] is the repeating digit |
| [latex]\text{4.161616}\ldots=4.\overline{16}[/latex] | [latex]16[/latex] is the repeating block |
| [latex]\text{0.271271271}\ldots =0.\overline{271}[/latex] | [latex]271[/latex] is the repeating block |
example
Write [latex]{\Large\frac{43}{22}}[/latex] as a decimal.Answer:
Solution
Divide [latex]43[/latex] by [latex]22[/latex]
 Notice that the differences of [latex]120[/latex] and [latex]100[/latex] repeat, so there is a repeat in the digits of the quotient; [latex]54[/latex] will repeat endlessly. The first decimal place in the quotient, [latex]9[/latex], is not part of the pattern. So,
[latex-display]{\Large\frac{43}{22}}=1.9\overline{54}[/latex-display]
Notice that the differences of [latex]120[/latex] and [latex]100[/latex] repeat, so there is a repeat in the digits of the quotient; [latex]54[/latex] will repeat endlessly. The first decimal place in the quotient, [latex]9[/latex], is not part of the pattern. So,
[latex-display]{\Large\frac{43}{22}}=1.9\overline{54}[/latex-display]
try it
[ohm_question]146259[/ohm_question]example
Simplify: [latex]{\Large\frac{7}{8}}+6.4[/latex]Answer: Solution
| [latex]{\Large\frac{7}{8}}+6.4[/latex] | ||
| Change [latex]\frac{7}{8}[/latex] to a decimal. |  |
[latex]0.875+6.4[/latex] |
| Add. | [latex]7.275[/latex] |
try it
[ohm_question]146261[/ohm_question] [ohm_question]146263[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Question ID 146263. 146261, 146259, 146257, 146253. Authored by: LumenLearning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 1: Convert a Fraction to a Decimal (terminating). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Ex 3: Convert a Fraction to a Decimal (repeating). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
