We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts Corequisite

Counting and Probability

Introduction

What you'll learn to do:  Apply counting formulas to calculate the probability of complex events

Counting? You already know how to count or you wouldn't be taking a college-level math class, right? Well yes, but what we'll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don't want to do this.

Learning Outcomes

  • Solve counting problems using permutations
  • Solve counting problems using combinations
  • Compute the probability of events within a complex counting problem
 

The Basic Counting Rule

We will start with some simple counting problems in order to develop the ideas that we will soon need.

example

Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pizza). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?   Solution 1: One way to solve this problem would be to systematically list each possible meal: soup + hamburger                   soup + sandwich                     soup + quiche soup + fajita                            soup + pizza                            salad + hamburger salad + sandwich                     salad + quiche                        salad + fajita salad + pizza                           breadsticks + hamburger         breadsticks + sandwich breadsticks + quiche               breadsticks + fajita                   breadsticks + pizza Assuming that we did this systematically and that we neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus you could go to the restaurant 15 nights in a row and have a different meal each night.   Solution 2: Another way to solve this problem would be to list all the possibilities in a table:
hamburger sandwich quiche fajita pizza
soup soup+burger
salad salad+burger
bread etc
In each of the cells in the table we could list the corresponding meal: soup + hamburger in the upper left corner, salad + hamburger below it, etc. But if we didn't really care what the possible meals are, only how many possible meals there are, we could just count the number of cells and arrive at an answer of 15, which matches our answer from the first solution. (It's always good when you solve a problem two different ways and get the same answer!)   Solution 3: We already have two perfectly good solutions. Why do we need a third?  The first method was not very systematic, and we might easily have made an omission. The second method was better, but suppose that in addition to the appetizer and the main course we further complicated the problem by adding desserts to the menu: we've used the rows of the table for the appetizers and the columns for the main courses—where will the desserts go? We would need a third dimension, and since drawing 3-D tables on a 2-D page or computer screen isn't terribly easy, we need a better way in case we have three categories to choose form instead of just two. So, what else can we do?  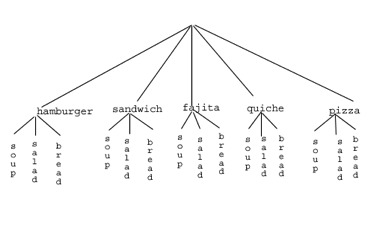Let's draw a tree diagram: Tree diagram of above table   This is called a "tree" diagram because at each stage we branch out, like the branches on a tree.  In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer).  We count the number of branches at the final level and get (surprise, surprise!) 15. If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.
  Tables and tree diagrams are a great way to visualize data, and these methods will continue to be useful in certain cases. But imagine a game where you have two decks of cards (with 52 cards in each deck) and you select one card from each deck. Would you really want to draw a table or tree diagram to determine the number of outcomes of this game? Let's go back to the previous example that involved selecting a meal from three appetizers and five main courses, and look at the second solution that used a table. Notice that one way to count the number of possible meals is simply to number each of the appropriate cells in the table, as we have done above. But another way to count the number of cells in the table would be multiply the number of rows (3) by the number of columns (5) to get 15. Notice that we could have arrived at the same result without making a table at all by simply multiplying the number of choices for the appetizer (3) by the number of choices for the main course (5). We generalize this technique as the basic counting rule:

Basic Counting Rule

If we are asked to choose one item from each of two separate categories where there are m items in the first category and n items in the second category, then the total number of available choices is m · n. This is sometimes called the multiplication rule for probabilities.

examples

Example 1: There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter?

Answer: There are 21 choices from the first category and 18 for the second, so there are 21 · 18 = 378 possibilities.

  The Basic Counting Rule can be extended when there are more than two categories by applying it repeatedly, as we see in the next example. Example 2: Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?

Answer: There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are 3 · 5 · 2 = 30 possibilities.

  Example 3: A quiz consists of 3 true-or-false questions.  In how many ways can a student answer the quiz?

Answer: There are 3 questions. Each question has 2 possible answers (true or false), so the quiz may be answered in 2 · 2 · 2 = 8 different ways.  Recall that another way to write 2 · 2 · 2 is 23, which is much more compact.

  These basic counting examples are described in the following video. https://youtu.be/fROqcu-ekkw
 

Try It

[ohm_question]7159[/ohm_question]
 

Permutations

Next, we will develop an even faster way to solve some of the problems we have already learned to solve by other means.  Let's start with an example.

example

How many different ways can the letters of the word MATH be rearranged to form a four-letter code word?

Answer: This problem is a bit different.  Instead of choosing one item from each of several different categories, we are repeatedly choosing items from the same category (the category is: the letters of the word MATH) and each time we choose an item we do not replace it, so there is one fewer choice at the next stage: we have 4 choices for the first letter (say we choose A), then 3 choices for the second (M, T and H; say we choose H), then 2 choices for the next letter (M and T; say we choose M) and only one choice at the last stage (T). Thus there are 4 · 3 · 2 · 1 = 24 ways to spell a code with with the letters MATH.

In the previous example, we needed to compute [latex]4\cdot3\cdot2\cdot1[/latex]. This type of calculation shows up often in mathematics so there is shorthand notation for it. The notation [latex]4![/latex] (which is read “four factorial”) is defined to be [latex]4!=4\cdot3\cdot2\cdot1[/latex].

Factorial

For a whole number n, the notation n! (read “n factorial”) is defined as: [latex]n!=n\cdot(n – 1)\cdot(n – 2)\dots3\cdot2\cdot1[/latex].

Try It

[ohm_question]7188[/ohm_question]

example

How many ways can five different door prizes be distributed among five people?

Answer: There are 5 choices of people to get the first door prize, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be 5! = 5 · 4 · 3 · 2 · 1 = 120 ways.

Try It

[ohm_question]7191[/ohm_question]
  Suppose, in thet last example, there were 10 people, but still only 5 door prizes.  Then there would be 10 choices of people to get the first door prize, 9 choices for the second, 8 choices for the third, 7 choices for the fourth, and 6 choices for the fifth door prize.  There are no prizes left, so the number of ways the prizes can be distributed will be [latex]10\cdot9\cdot8\cdot7\cdot6[/latex].  We are essentially choosing 5 people in order to win the 5 door prizes and no one can win more than 1 prize. There is a special notation and definition to describe this situation where we are choosing r items out of n possibilities without replacement and where the order of selection is important.

Permutations

We define the notation [latex]{}_{n}{{P}_{r}}[/latex] as follows: [latex]{}_{n}{{P}_{r}}=n\cdot(n – 1)\cdot(n – 2)\dots(n – r + 1).[/latex]

We say that there are [latex]{}_{n}{{P}_{r}}[/latex] permutations of size r that may be selected from among n choices without replacement when order matters. It turns out that we can express this result more simply using factorials.

[latex]{}_{n}{{P}_{r}}=\frac{n!}{(n-r)!}[/latex]

Examples

Example 1: I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this?

Answer: Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are 9P4 = 9 · 8 · 7 · 6 = 3,024 permutations.

  Example 2: How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization?

Answer: We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is 16P4 = 16 · 15 · 14 · 13 = 43,680.

  View this video to see more about the permutations examples. https://youtu.be/xlyX2UJMJQI

Try It

[ohm_question]7193[/ohm_question]
 

Combinations

In the previous section we considered the situation where we chose r items out of n possibilities without replacement and where the order of selection was important. We now consider a similar situation in which the order of selection is not important.

Combinations

We define the notation [latex]{}_{n}{{C}_{r}}[/latex] as follows: [latex]{}_{n}{{C}_{r}}=\frac{n!}{(n-r)!r!}[/latex].

We say that there are [latex]{}_{n}{{C}_{r}}[/latex] combinations of size r that may be selected from among n choices without replacement where order doesn’t matter.  

Example

A group of four students is to be chosen from a 35-member class to represent the class on the student council. How many ways can this be done?

Answer: Since we are choosing 4 people out of 35 without replacement where the order of selection is not important there are [latex]{}_{35}{{C}_{4}}=\frac{35\cdot34\cdot33\cdot32}{4\cdot3\cdot2\cdot1}[/latex] = 52,360 combinations.

 

Example

The United States Senate Appropriations Committee consists of 29 members, 15 Republicans and 14 Democrats. The Defense Subcommittee consists of 19 members, 10 Republicans and 9 Democrats. How many different ways can the members of the Defense Subcommittee be chosen from among the 29 Senators on the Appropriations Committee?

Answer: In this case we need to choose 10 of the 15 Republicans and 9 of the 14 Democrats.  There are 15C10 = 3003 ways to choose the 10 Republicans and 14C9 = 2002 ways to choose the 9 Democrats.   But now what?  How do we finish the problem? Suppose we listed all of the possible 10-member Republican groups on 3003 slips of red paper and  all of the possible 9-member Democratic groups on 2002 slips of blue paper.  How many ways can we choose one red slip and one blue slip?  This is a job for the Basic Counting Rule!  We are simply making one choice from the first category and one choice from the second category, just like in the restaurant menu problems from earlier. There must be 3003 · 2002 = 6,012,006 possible ways of selecting the members of the Defense Subcommittee.

This example is worked through below. https://youtu.be/Xqc2sdYN7xo
 

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously