Modeling and Finding Equivalent Fractions
Learning Outcomes
- Use fraction tiles or visual aids to create equivalent fractions
- Find an equivalent fraction given a fraction
Equivalent Fractions
Equivalent fractions are fractions that have the same value. Since two [latex]{\Large\frac{1}{4}}[/latex] tiles cover the [latex]{\Large\frac{1}{2}}[/latex] tile, we see that [latex]{\Large\frac{2}{4}}[/latex] is the same as [latex]{\Large\frac{1}{2}}[/latex], or [latex]{\Large\frac{2}{4}}={\Large\frac{1}{2}}[/latex].
Since two [latex]{\Large\frac{1}{4}}[/latex] tiles cover the [latex]{\Large\frac{1}{2}}[/latex] tile, we see that [latex]{\Large\frac{2}{4}}[/latex] is the same as [latex]{\Large\frac{1}{2}}[/latex], or [latex]{\Large\frac{2}{4}}={\Large\frac{1}{2}}[/latex].
 Since three [latex]{\Large\frac{1}{6}}[/latex] tiles cover the [latex]{\Large\frac{1}{2}}[/latex] tile, we see that [latex]{\Large\frac{3}{6}}[/latex] is the same as [latex]{\Large\frac{1}{2}}[/latex].
Since three [latex]{\Large\frac{1}{6}}[/latex] tiles cover the [latex]{\Large\frac{1}{2}}[/latex] tile, we see that [latex]{\Large\frac{3}{6}}[/latex] is the same as [latex]{\Large\frac{1}{2}}[/latex].
Example
Use fraction tiles to find equivalent fractions. Show your result with a figure.- How many eighths ([latex]{\Large\frac{1}{8}}[/latex]) equal one-half ([latex]{\Large\frac{1}{2}}[/latex])?
- How many tenths ([latex]{\Large\frac{1}{10}}[/latex]) equal one-half ([latex]{\Large\frac{1}{2}}[/latex])?
- How many twelfths ([latex]{\Large\frac{1}{12}}[/latex]) equal one-half ([latex]{\Large\frac{1}{2}}[/latex])?
 2. It takes five [latex]{\Large\frac{1}{10}}[/latex] tiles to exactly cover the [latex]{\Large\frac{1}{2}}[/latex] tile, so [latex]{\Large\frac{5}{10}}={\Large\frac{1}{2}}[/latex].
2. It takes five [latex]{\Large\frac{1}{10}}[/latex] tiles to exactly cover the [latex]{\Large\frac{1}{2}}[/latex] tile, so [latex]{\Large\frac{5}{10}}={\Large\frac{1}{2}}[/latex].
 3. It takes six [latex]{\Large\frac{1}{12}}[/latex] tiles to exactly cover the [latex]{\Large\frac{1}{2}}[/latex] tile, so [latex]{\Large\frac{6}{12}}={\Large\frac{1}{2}}[/latex].
3. It takes six [latex]{\Large\frac{1}{12}}[/latex] tiles to exactly cover the [latex]{\Large\frac{1}{2}}[/latex] tile, so [latex]{\Large\frac{6}{12}}={\Large\frac{1}{2}}[/latex].

Try it
[ohm_question height="270"]146001[/ohm_question]Find Equivalent Fractions
We used fraction tiles to show that there are many fractions equivalent to [latex]{\Large\frac{1}{2}}[/latex]. For example, [latex]{\Large\frac{2}{4},\frac{3}{6}}[/latex], and [latex]{\Large\frac{4}{8}}[/latex] are all equivalent to [latex]{\Large\frac{1}{2}}[/latex]. When we lined up the fraction tiles, it took four of the [latex]{\Large\frac{1}{8}}[/latex] tiles to make the same length as a [latex]{\Large\frac{1}{2}}[/latex] tile. This showed that [latex]{\Large\frac{4}{8}}={\Large\frac{1}{2}}[/latex]. See the previous example. We can show this with pizzas, too. Image (a) shows a single pizza, cut into two equal pieces with [latex]{\Large\frac{1}{2}}[/latex] shaded. Image (b) shows a second pizza of the same size, cut into eight pieces with [latex]{\Large\frac{4}{8}}[/latex] shaded.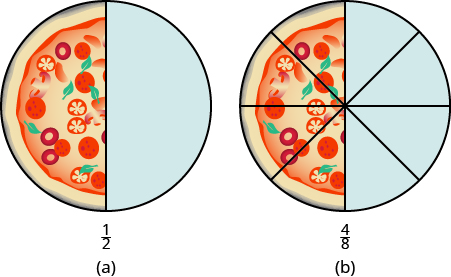 This is another way to show that [latex]{\Large\frac{1}{2}}[/latex] is equivalent to [latex]{\Large\frac{4}{8}}[/latex].
How can we use mathematics to change [latex]{\Large\frac{1}{2}}[/latex] into [latex]{\Large\frac{4}{8}}[/latex]? How could you take a pizza that is cut into two pieces and cut it into eight pieces? You could cut each of the two larger pieces into four smaller pieces! The whole pizza would then be cut into eight pieces instead of just two. Mathematically, what we’ve described could be written as:
This is another way to show that [latex]{\Large\frac{1}{2}}[/latex] is equivalent to [latex]{\Large\frac{4}{8}}[/latex].
How can we use mathematics to change [latex]{\Large\frac{1}{2}}[/latex] into [latex]{\Large\frac{4}{8}}[/latex]? How could you take a pizza that is cut into two pieces and cut it into eight pieces? You could cut each of the two larger pieces into four smaller pieces! The whole pizza would then be cut into eight pieces instead of just two. Mathematically, what we’ve described could be written as:
[latex]{\Large\frac{1\cdot\color{blue}{4}}{2\cdot\color{blue}{4}}}={\Large\frac{4}{8}}[/latex]
These models lead to the Equivalent Fractions Property, which states that if we multiply the numerator and denominator of a fraction by the same number, the value of the fraction does not change.Equivalent Fractions Property
If [latex]a,b[/latex], and [latex]c[/latex] are numbers where [latex]b\ne 0[/latex] and [latex]c\ne 0[/latex], then [latex-display]{\Large\frac{a}{b}}={\Large\frac{a\cdot c}{b\cdot c}}[/latex-display][latex]{\Large\frac{1\cdot\color{blue}{3}}{2\cdot\color{blue}{3}}}={\Large\frac{3}{6}}[/latex] so [latex]{\Large\frac{1}{2}}={\Large\frac{3}{6}}[/latex]
[latex]{\Large\frac{1\cdot\color{blue}{2}}{2\cdot\color{blue}{2}}}={\Large\frac{2}{4}}[/latex] so [latex]{\Large\frac{1}{2}}={\Large\frac{2}{4}}[/latex]
[latex]{\Large\frac{1\cdot\color{blue}{10}}{2\cdot\color{blue}{10}}}={\Large\frac{10}{20}}[/latex] so [latex]{\Large\frac{1}{2}}={\Large\frac{10}{20}}[/latex]
So, we say that [latex]{\Large\frac{1}{2},\frac{2}{4},\frac{3}{6}}[/latex], and [latex]{\Large\frac{10}{20}}[/latex] are equivalent fractions.Example
Find three fractions equivalent to [latex]{\Large\frac{2}{5}}[/latex].Answer: Solution To find a fraction equivalent to [latex]{\Large\frac{2}{5}}[/latex], we multiply the numerator and denominator by the same number (but not zero). Let us multiply them by [latex]2,3[/latex], and [latex]5[/latex]. [latex-display]{\Large\frac{2\cdot\color{blue}{2}}{5\cdot\color{blue}{2}}}={\Large\frac{4}{10}}[/latex] [latex]{\Large\frac{2\cdot\color{blue}{3}}{5\cdot\color{blue}{3}}}={\Large\frac{6}{15}}[/latex] [latex]{\Large\frac{2\cdot\color{blue}{5}}{5\cdot\color{blue}{5}}}={\Large\frac{10}{25}}[/latex-display] So, [latex]{\Large\frac{4}{10},\frac{6}{15}}[/latex], and [latex]{\Large\frac{10}{25}}[/latex] are equivalent to [latex]{\Large\frac{2}{5}}[/latex].
Try it
Find three fractions equivalent to [latex]{\Large\frac{3}{5}}[/latex].Answer: Correct answers include [latex]{\Large\frac{6}{10},\frac{9}{15}},\text{and }{\Large\frac{12}{20}}[/latex].
Find three fractions equivalent to [latex]{\Large\frac{4}{5}}[/latex].Answer: Correct answers include [latex]{\Large\frac{8}{10},\frac{12}{15}},\text{and }{\Large\frac{16}{20}}[/latex].
Example
Find a fraction with a denominator of [latex]21[/latex] that is equivalent to [latex]{\Large\frac{2}{7}}[/latex].Answer: Solution To find equivalent fractions, we multiply the numerator and denominator by the same number. In this case, we need to multiply the denominator by a number that will result in [latex]21[/latex]. Since we can multiply [latex]7[/latex] by [latex]3[/latex] to get [latex]21[/latex], we can find the equivalent fraction by multiplying both the numerator and denominator by [latex]3[/latex].
[latex]{\Large\frac{2}{7}}={\Large\frac{2\cdot\color{blue}{3}}{7\cdot\color{blue}{3}}}={\Large\frac{6}{21}}[/latex]
Try it
[ohm_question height="270"]146005[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Question ID: 146001, 146005. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Ex: Determine Equivalent Fractions. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
