Linear Systems in Two Variables
Learning Objectives
- Define and classify solutions to systems of linear equations
- Recognize consistent and inconsistent, dependent and independent systems of linear equations
- Determine whether an ordered pair is a solution to a system of linear equations
- Solve a system of linear equations by graphing
- Methods for solving systems
- Use substitution to solve a system algebraically
- Solve a system using the addition method
- Recognize when a system is inconsistent from algebraic results
- Recognize when a system is dependent using algebraic results
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables, and three types of solutions.- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
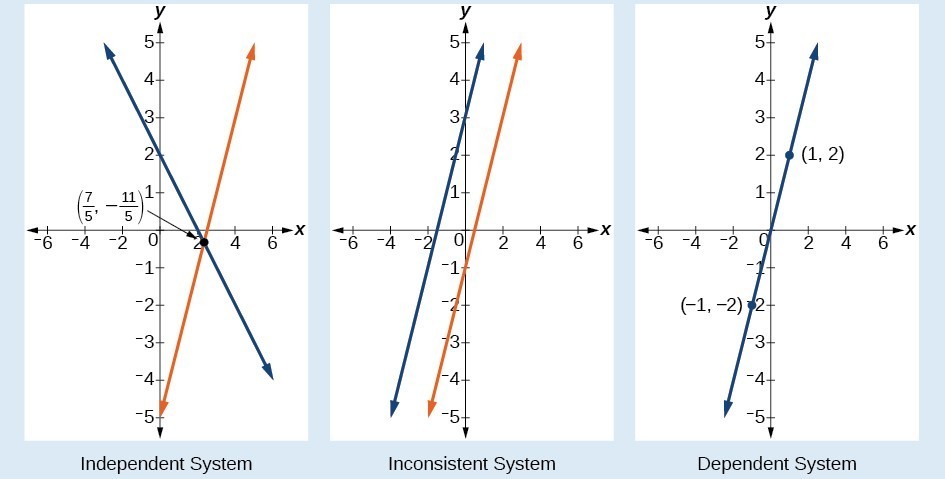 The independent and dependent systems are also consistent because they both have at least one solution.
The independent and dependent systems are also consistent because they both have at least one solution.
How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution.
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
Example
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.Answer: Substitute the ordered pair [latex]\left(5,1\right)[/latex] into both equations.
[latex]\begin{array}{ll}\left(5\right)+3\left(1\right)=8\hfill & \hfill \\ \text{ }8=8\hfill & \text{True}\hfill \\ 2\left(5\right)-9=\left(1\right)\hfill & \hfill \\ \text{ }\text{1=1}\hfill & \text{True}\hfill \end{array}[/latex]
The ordered pair [latex]\left(5,1\right)[/latex] satisfies both equations, so it is the solution to the system. We can see the solution clearly by plotting the graph of each equation. Since the solution is an ordered pair that satisfies both equations, it is a point on both of the lines and thus the point of intersection of the two lines.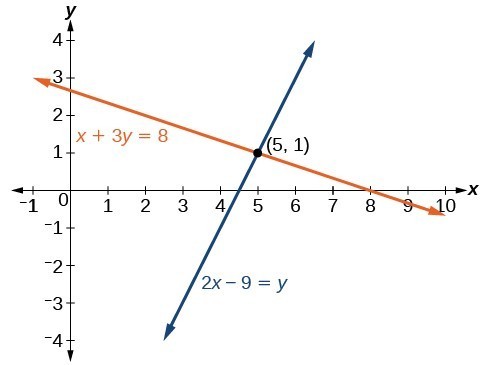
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.Example
Solve the following system of equations by graphing. Identify the type of system.[latex]\begin{array}{c}2x+y=-8\\ x-y=-1\end{array}[/latex]
Answer: Solve the first equation for [latex]y[/latex].
[latex]\begin{array}{c}2x+y=-8\\ y=-2x - 8\end{array}[/latex]
Solve the second equation for [latex]y[/latex].[latex]\begin{array}{c}x-y=-1\\ y=x+1\end{array}[/latex]
Graph both equations on the same set of axes as in the figure below.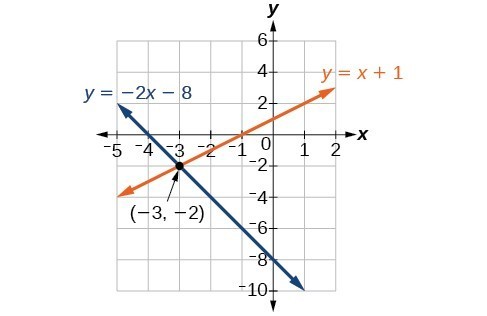 The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex]. We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations
The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex]. We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations
[latex]\begin{array}{ll}2\left(-3\right)+\left(-2\right)=-8\hfill & \hfill \\ \text{ }-8=-8\hfill & \text{True}\hfill \\ \text{ }\left(-3\right)-\left(-2\right)=-1\hfill & \hfill \\ \text{ }-1=-1\hfill & \text{True}\hfill \end{array}[/latex]
The solution to the system is the ordered pair [latex]\left(-3,-2\right)[/latex], so the system is independent.Substitution
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example
Solve the following system of equations by substitution.Answer: First, we will solve the first equation for [latex]y[/latex].
[latex]\begin{array}{llll}-x+y=-5\hfill & \hfill & \hfill & \hfill \\ -\left(8\right)+\left(3\right)=-5\hfill & \hfill & \hfill & \text{True}\hfill \\ 2x - 5y=1\hfill & \hfill & \hfill & \hfill \\ 2\left(8\right)-5\left(3\right)=1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex]
The substitution method can be used to solve any linear system in two variables, but the method works best if one of the equations contains a coefficient of 1 or [latex]–1[/latex] so that we do not have to deal with fractions.Example
Solve the following system of equations.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
Answer: We can approach this problem in two ways. Because one equation is already solved for x, the most obvious step is to use substitution.
[latex]\begin{array}{r}x+2y=13\hfill \\ \left(9 - 2y\right)+2y=13\hfill \\ 9+0y=13\hfill \\ 9=13\hfill \end{array}[/latex]
Clearly, this statement is a contradiction because [latex]9\ne 13[/latex]. Therefore, the system has no solution. The second approach would be to first manipulate the equations so that they are both in slope-intercept form. We manipulate the first equation as follows.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ 2y=-x+9\hfill \\ \text{ }y=-\frac{1}{2}x+\frac{9}{2}\hfill \end{array}[/latex]
We then convert the second equation expressed to slope-intercept form.[latex]\begin{array}{l}x+2y=13\hfill \\ \text{ }2y=-x+13\hfill \\ \text{ }y=-\frac{1}{2}x+\frac{13}{2}\hfill \end{array}[/latex]
Comparing the equations, we see that they have the same slope but different y-intercepts. Therefore, the lines are parallel and do not intersect.[latex]\begin{array}{l}\begin{array}{l}\\ y=-\frac{1}{2}x+\frac{9}{2}\end{array}\hfill \\ y=-\frac{1}{2}x+\frac{13}{2}\hfill \end{array}[/latex]
Writing the equations in slope-intercept form confirms that the system is inconsistent because all lines will intersect eventually unless they are parallel. Parallel lines will never intersect; thus, the two lines have no points in common. The graphs of the equations in this example are shown below.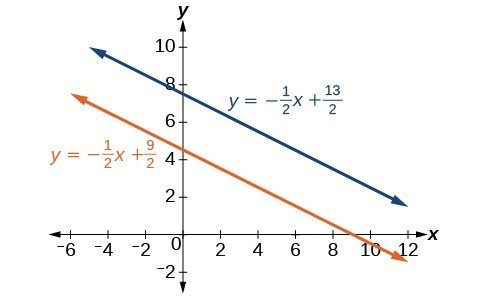
Answer
There is no solution to this system of linear equations.Solving Systems of Equations in Two Variables by the Addition Method
A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.How To: Given a system of equations, solve using the addition method.
- Write both equations with x- and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Example: Solving a System by the Addition Method
Solve the given system of equations by addition. [latex-display]\begin{array}{l}x+2y=-1\hfill \\ -x+y=3\hfill \end{array}[/latex-display]Answer: Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, –1, is the opposite of the coefficient of [latex]x[/latex] in the first equation, 1. We can add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant. [latex-display]\frac{\begin{array}{l}\hfill \\ x+2y=-1\hfill \\ -x+y=3\hfill \end{array}}{\text{}\text{}\text{}\text{}\text{}3y=2}[/latex-display] Now that we have eliminated [latex]x[/latex], we can solve the resulting equation for [latex]y[/latex]. [latex-display]\begin{array}{l}3y=2\hfill \\ \text{ }y=\frac{2}{3}\hfill \end{array}[/latex-display] Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex]. [latex-display]\begin{array}{l}\text{ }-x+y=3\hfill \\ \text{ }-x+\frac{2}{3}=3\hfill \\ \text{ }-x=3-\frac{2}{3}\hfill \\ \text{ }-x=\frac{7}{3}\hfill \\ \text{ }x=-\frac{7}{3}\hfill \end{array}[/latex-display] The solution to this system is [latex]\left(-\frac{7}{3},\frac{2}{3}\right)[/latex]. Check the solution in the first equation. [latex-display]\begin{array}{llll}\text{ }x+2y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }\left(-\frac{7}{3}\right)+2\left(\frac{2}{3}\right)=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\frac{7}{3}+\frac{4}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\frac{3}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-1=-1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex-display]
Analysis of the Solution
We gain an important perspective on systems of equations by looking at the graphical representation. See the graph below to find that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.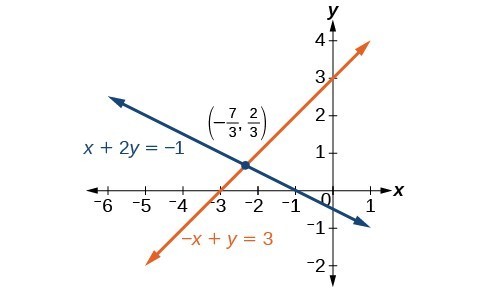
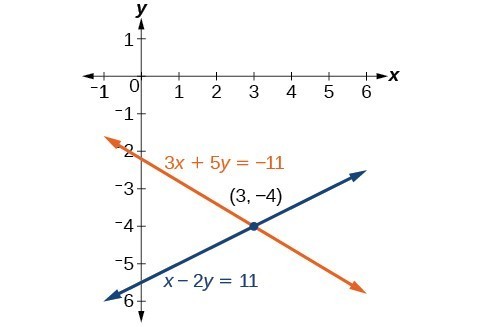
Example: Using the Addition Method When Multiplication of One Equation Is Required
Solve the given system of equations by the addition method. [latex-display]\begin{array}{l}3x+5y=-11\hfill \\ \hfill \\ x - 2y=11\hfill \end{array}[/latex-display]Answer:
Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the x-terms will add to zero.
[latex-display]\begin{array}{llll}\text{ }x - 2y=11\hfill & \hfill & \hfill & \hfill \\ -3\left(x - 2y\right)=-3\left(11\right)\hfill & \hfill & \hfill & \text{Multiply both sides by }-3.\hfill \\ \text{ }-3x+6y=-33\hfill & \hfill & \hfill & \text{Use the distributive property}.\hfill \end{array}[/latex-display]
Now, let’s add them.
[latex-display]\begin{array}\ \hfill 3x+5y=−11 \\ \hfill −3x+6y=−33 \\ \text{_____________} \\ \hfill 11y=−44 \\ \hfill y=−4 \end{array}[/latex-display]
For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex].
[latex-display]\begin{array}{c}3x+5y=-11\\ 3x+5\left(-4\right)=-11\\ 3x - 20=-11\\ 3x=9\\ x=3\end{array}[/latex-display]
Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation.
[latex-display]\begin{array}{llll}\text{ }x - 2y=11\hfill & \hfill & \hfill & \hfill \\ \left(3\right)-2\left(-4\right)=3+8\hfill & \hfill & \hfill & \hfill \\ \text{ }=11\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex-display]
Try It
Solve the system of equations by addition. [latex-display]\begin{array}{c}2x - 7y=2\\ 3x+y=-20\end{array}[/latex-display]Answer: [latex]\left(-6,-2\right)[/latex]
Example: Using the Addition Method When Multiplication of Both Equations Is Required
Solve the given system of equations in two variables by addition. [latex-display]\begin{array}{c}2x+3y=-16\\ 5x - 10y=30\end{array}[/latex-display]Answer:
One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. The least common multiple is [latex]10x[/latex] so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex].
[latex-display]\begin{array}{l} -5\left(2x+3y\right)=-5\left(-16\right)\hfill \\ \text{ }-10x - 15y=80\hfill \\ \text{ }2\left(5x - 10y\right)=2\left(30\right)\hfill \\ \text{ }10x - 20y=60\hfill \end{array}[/latex-display]
Then, we add the two equations together.
[latex-display]\begin{array}\ −10x−15y=80 \\ 10x−20y=60 \\ \text{______________} \\ \text{ }−35y=140 \\ y=−4 \end{array}[/latex-display]
Substitute [latex]y=-4[/latex] into the original first equation.
[latex-display]\begin{array}{c}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{array}[/latex-display]
The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the other equation.
[latex-display]\begin{array}{r}\hfill \text{ }5x - 10y=30\\ \hfill 5\left(-2\right)-10\left(-4\right)=30\\ \hfill \text{ }-10+40=30\\ \hfill \text{ }30=30\end{array}[/latex-display]

Example: Using the Addition Method in Systems of Equations Containing Fractions
Solve the given system of equations in two variables by addition. [latex-display]\begin{array}{l}\frac{x}{3}+\frac{y}{6}=3\hfill \\ \frac{x}{2}-\frac{y}{4}=\text{ }1\hfill \end{array}[/latex-display]Answer: First clear each equation of fractions by multiplying both sides of the equation by the least common denominator. [latex-display]\begin{array}{l}6\left(\frac{x}{3}+\frac{y}{6}\right)=6\left(3\right)\hfill \\ \text{ }2x+y=18\hfill \\ 4\left(\frac{x}{2}-\frac{y}{4}\right)=4\left(1\right)\hfill \\ \text{ }2x-y=4\hfill \end{array}[/latex-display] Now multiply the second equation by [latex]-1[/latex] so that we can eliminate the x-variable. [latex-display]\begin{array}{l}-1\left(2x-y\right)=-1\left(4\right)\hfill \\ \text{ }-2x+y=-4\hfill \end{array}[/latex-display] Add the two equations to eliminate the x-variable and solve the resulting equation. [latex-display]\begin{array}\ \hfill 2x+y=18 \\ \hfill−2x+y=−4 \\ \text{_____________} \\ \hfill 2y=14 \\ \hfill y=7 \end{array}[/latex-display] Substitute [latex]y=7[/latex] into the first equation. [latex-display]\begin{array}{l}2x+\left(7\right)=18\hfill \\ \text{ }2x=11\hfill \\ \text{ }x=\frac{11}{2}\hfill \\ \text{ }=7.5\hfill \end{array}[/latex-display] The solution is [latex]\left(\frac{11}{2},7\right)[/latex]. Check it in the other equation. [latex-display]\begin{array}{c}\frac{x}{2}-\frac{y}{4}=1\\ \frac{\frac{11}{2}}{2}-\frac{7}{4}=1\\ \frac{11}{4}-\frac{7}{4}=1\\ \frac{4}{4}=1\end{array}[/latex-display]
Try It
Solve the system of equations by addition. [latex-display]\begin{array}{c}2x+3y=8\\ 3x+5y=10\end{array}[/latex-display]Answer: [latex]\left(10,-4\right)[/latex]
Classify Solutions to Systems
Now that we have several methods for solving systems of equations, we can use the methods to identify inconsistent systems. Recall that an inconsistent system consists of parallel lines that have the same slope but different [latex]y[/latex] -intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement, such as [latex]12=0[/latex].Example: Solving an Inconsistent System of Equations
Solve the following system of equations.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
Answer: We can approach this problem in two ways. Because one equation is already solved for [latex]x[/latex], the most obvious step is to use substitution.
[latex]\begin{array}{l}x+2y=13\hfill \\ \left(9 - 2y\right)+2y=13\hfill \\ 9+0y=13\hfill \\ 9=13\hfill \end{array}[/latex]
Clearly, this statement is a contradiction because [latex]9\ne 13[/latex]. Therefore, the system has no solution. The second approach would be to first manipulate the equations so that they are both in slope-intercept form. We manipulate the first equation as follows.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ 2y=-x+9\hfill \\ \text{ }y=-\frac{1}{2}x+\frac{9}{2}\hfill \end{array}[/latex]
We then convert the second equation expressed to slope-intercept form.[latex]\begin{array}{l}x+2y=13\hfill \\ \text{ }2y=-x+13\hfill \\ \text{ }y=-\frac{1}{2}x+\frac{13}{2}\hfill \end{array}[/latex]
Comparing the equations, we see that they have the same slope but different y-intercepts. Therefore, the lines are parallel and do not intersect.[latex]\begin{array}{l}\begin{array}{l}\\ y=-\frac{1}{2}x+\frac{9}{2}\end{array}\hfill \\ y=-\frac{1}{2}x+\frac{13}{2}\hfill \end{array}[/latex]
Analysis of the Solution
Writing the equations in slope-intercept form confirms that the system is inconsistent because all lines will intersect eventually unless they are parallel. Parallel lines will never intersect; thus, the two lines have no points in common. The graphs of the equations in this example are shown below.
Try It
Solve the following system of equations in two variables.[latex]\begin{array}{l}2y - 2x=2\\ 2y - 2x=6\end{array}[/latex]
Answer: No solution. It is an inconsistent system.
Expressing the Solution of a System of Dependent Equations Containing Two Variables
Recall that a dependent system of equations in two variables is a system in which the two equations represent the same line. Dependent systems have an infinite number of solutions because all of the points on one line are also on the other line. After using substitution or addition, the resulting equation will be an identity, such as [latex]0=0[/latex].Example: Finding a Solution to a Dependent System of Linear Equations
Find a solution to the system of equations using the addition method.[latex]\begin{array}{c}x+3y=2\\ 3x+9y=6\end{array}[/latex]
Answer: With the addition method, we want to eliminate one of the variables by adding the equations. In this case, let’s focus on eliminating [latex]x[/latex]. If we multiply both sides of the first equation by [latex]-3[/latex], then we will be able to eliminate the [latex]x[/latex] -variable.
[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \left(-3\right)\left(x+3y\right)=\left(-3\right)\left(2\right)\hfill \\ \text{ }-3x - 9y=-6\hfill \end{array}[/latex]
Now add the equations.[latex]\begin{array} \hfill−3x−9y=−6 \\ \hfill+3x+9y=6 \\ \hfill \text{_____________} \\ \hfill 0=0 \end{array}[/latex]
We can see that there will be an infinite number of solutions that satisfy both equations.Analysis of the Solution
If we rewrote both equations in the slope-intercept form, we might know what the solution would look like before adding. Let’s look at what happens when we convert the system to slope-intercept form.[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \text{ }3y=-x+2\hfill \\ \text{ }y=-\frac{1}{3}x+\frac{2}{3}\hfill \\ 3x+9y=6\hfill \\ \text{ }9y=-3x+6\hfill \\ \text{ }y=-\frac{3}{9}x+\frac{6}{9}\hfill \\ \text{ }y=-\frac{1}{3}x+\frac{2}{3}\hfill \end{array}[/latex]
Look at the graph below. Notice the results are the same. The general solution to the system is [latex]\left(x, -\frac{1}{3}x+\frac{2}{3}\right)[/latex].
Writing the general solution
In the previous example, we presented an analysis of the solution to the following system of equations:[latex]\begin{array}{c}x+3y=2\\ 3x+9y=6\end{array}[/latex]
After a little algebra, we found that these two equations were exactly the same. We then wrote the general solution as [latex]\left(x, -\frac{1}{3}x+\frac{2}{3}\right)[/latex]. Why would we write the solution this way? In some ways, this representation tells us a lot. It tells us that x can be anything, x is x. It also tells us that y is going to depend on x, just like when we write a function rule. In this case, depending on what you put in for x, y will be defined in terms of x as [latex]-\frac{1}{3}x+\frac{2}{3}[/latex]. In other words, there are infinitely many (x,y) pairs that will satisfy this system of equations, and they all fall on the line [latex]y=-\frac{1}{3}x+\frac{2}{3}[/latex].Try It
Solve the following system of equations in two variables.[latex]\begin{array}{l}\begin{array}{l}\\ \text{ }\text{}\text{}y - 2x=5\end{array}\hfill \\ -3y+6x=-15\hfill \end{array}[/latex]
Answer: The system is dependent so there are infinite solutions of the form [latex]\left(x,2x+5\right)[/latex].
Licenses & Attributions
CC licensed content, Original
- Determine if an Ordered Pair is a Solution to a System of Linear Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Determine the Number of Solutions to a System of Linear Equations From a Graph. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Solve a System of Equations by Graphing. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 2: Solve a System of Equations Using Substitution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - No Solution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve an Application Problem Using a System of Linear Equations (09x-43). Authored by: James Sousa (Mathispower4u.com) . License: Public Domain: No Known Copyright.
- Ex 1: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Eliminations (Fractions). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: System of Equations Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: System of Equations Using Elimination (No Solution). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- College Algebra. Provided by: Open Stax Authored by: Abramson, Jay et al... Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free: http://cnx.org/contents/[email protected].
- Question ID 29699. Authored by: McClure, Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 115164, 115120, 115110. Authored by: Shabazian, Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
