Imaginary and Complex Numbers
Learning Outcomes
- Express roots of negative numbers in terms of [latex]i[/latex]
- Express imaginary numbers as [latex]bi[/latex] and complex numbers as [latex]a+bi[/latex]
[latex] i=\sqrt{-1}[/latex]
Because [latex] \sqrt{x}\,\cdot \,\sqrt{x}=x[/latex], we can also see that [latex] \sqrt{-1}\,\cdot \,\sqrt{-1}=-1[/latex] or [latex] i\,\cdot \,i=-1[/latex]. We also know that [latex] i\,\cdot \,i={{i}^{2}}[/latex], so we can conclude that [latex] {{i}^{2}}=-1[/latex].[latex] {{i}^{2}}=-1[/latex]
The number [latex]−1[/latex] allows us to work with roots of all negative numbers, not just [latex] \sqrt{-1}[/latex]. There are two important rules to remember: [latex] \sqrt{-1}=i[/latex], and [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex]. You will use these rules to rewrite the square root of a negative number as the square root of a positive number times [latex] \sqrt{-1}[/latex]. Next you will simplify the square root and rewrite [latex] \sqrt{-1}[/latex] as [latex]i[/latex]. Let us try an example.Example
Simplify. [latex] \sqrt{-4}[/latex]Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] \sqrt{-4}=\sqrt{4\cdot -1}=\sqrt{4}\sqrt{-1}[/latex-display] Since [latex]4[/latex] is a perfect square [latex](4=2^{2})[/latex], you can simplify the square root of [latex]4[/latex]. [latex-display] \sqrt{4}\sqrt{-1}=2\sqrt{-1}[/latex-display] Use the definition of [latex]i[/latex] to rewrite [latex] \sqrt{-1}[/latex] as [latex]i[/latex]. [latex-display] 2\sqrt{-1}=2i[/latex-display] The answer is [latex]2i[/latex].
Example
Simplify. [latex] \sqrt{-18}[/latex]Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] \sqrt{-18}=\sqrt{18\cdot -1}=\sqrt{18}\sqrt{-1}[/latex-display] Since [latex]18[/latex] is not a perfect square, use the same rule to rewrite it using factors that are perfect squares. In this case, [latex]9[/latex] is the only perfect square factor, and the square root of [latex]9[/latex] is [latex]3[/latex]. [latex-display] \sqrt{18}\sqrt{-1}=\sqrt{9}\sqrt{2}\sqrt{-1}=3\sqrt{2}\sqrt{-1}[/latex-display] Use the definition of [latex]i[/latex] to rewrite [latex] \sqrt{-1}[/latex] as [latex]i[/latex]. [latex-display] 3\sqrt{2}\sqrt{-1}=3\sqrt{2}i=3i\sqrt{2}[/latex-display] Remember to write [latex]i[/latex] in front of the radical. The answer is [latex]3i\sqrt[{}]{2}[/latex].
Example
Simplify. [latex] -\sqrt{-72}[/latex]Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] -\sqrt{-72}=-\sqrt{72\cdot -1}=-\sqrt{72}\sqrt{-1}[/latex-display] Since [latex]72[/latex] is not a perfect square, use the same rule to rewrite it using factors that are perfect squares. Notice that [latex]72[/latex] has three perfect squares as factors: [latex]4, 9[/latex], and [latex]36[/latex]. It is easiest to use the largest factor that is a perfect square. [latex-display] -\sqrt{72}\sqrt{-1}=-\sqrt{36}\sqrt{2}\sqrt{-1}=-6\sqrt{2}\sqrt{-1}[/latex-display] Use the definition of [latex]i[/latex] to rewrite [latex] \sqrt{-1}[/latex] as [latex]i[/latex]. [latex-display] -6\sqrt{2}\sqrt{-1}=-6\sqrt{2}i=-6i\sqrt{2}[/latex-display] Remember to write [latex]i[/latex] in front of the radical. The answer is [latex]-6i\sqrt{2}[/latex]
Rewriting the Square Root of a Negative Number
- Find perfect squares within the radical.
- Rewrite the radical using the rule [latex] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
- Rewrite [latex] \sqrt{-1}[/latex] as [latex]i[/latex].
Try It
[ohm_question]3907[/ohm_question]Complex Numbers
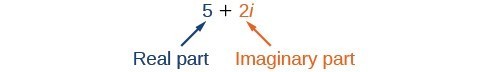
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written [latex]a+bi[/latex] where [latex]a[/latex] is the real part and [latex]bi[/latex] is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4i\sqrt{3}[/latex].
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers. You can use the usual operations (addition, subtraction, multiplication, and so on) with imaginary numbers. You will see more of that later.
| Complex Number | Real Part | Imaginary Part |
|---|---|---|
| [latex]3+7i[/latex] | [latex]3[/latex] | [latex]7i[/latex] |
| [latex]18–32i[/latex] | [latex]18[/latex] | [latex]−32i[/latex] |
| [latex] -\frac{3}{5}+i\sqrt{2}[/latex] | [latex] -\frac{3}{5}[/latex] | [latex] i\sqrt{2}[/latex] |
| [latex] \frac{\sqrt{2}}{2}-\frac{1}{2}i[/latex] | [latex] \frac{\sqrt{2}}{2}[/latex] | [latex]-\frac{1}{2}i[/latex] |
| Number | Complex Form: [latex]a+bi[/latex] | Real Part | Imaginary Part |
|---|---|---|---|
| [latex]17[/latex] | [latex]17+0i[/latex] | [latex]17[/latex] | [latex]0i[/latex] |
| [latex]−3i[/latex] | [latex]0–3i[/latex] | [latex]0[/latex] | [latex]−3i[/latex] |
Example
Write [latex]83.6[/latex] as a complex number.Answer: Remember that a complex number has the form [latex]a+bi[/latex]. You need to figure out what a and b need to be. [latex-display]a+bi[/latex-display] Since [latex]83.6[/latex] is a real number, it is the real part (a) of the complex number [latex]a+bi[/latex]. [latex-display]83.6+bi[/latex-display] A real number does not contain any imaginary parts, so the value of [latex]b[/latex] is [latex]0[/latex]. The answer is [latex]83.6+0i[/latex].
Try It
[ohm_question]197339[/ohm_question]Example
Write [latex]−3i[/latex] as a complex number.Answer: Remember that a complex number has the form [latex]a+bi[/latex]. You need to figure out what [latex]a[/latex] and [latex]b[/latex] need to be. [latex-display]a+bi[/latex-display] Since [latex]−3i[/latex] is an imaginary number, it is the imaginary part [latex]bi[/latex] of the complex number [latex]a+bi[/latex]. [latex-display]a–3i[/latex-display] This imaginary number has no real parts, so the value of [latex]a[/latex] is [latex]0[/latex]. The answer is [latex]0–3i[/latex].
Summary
Square roots of negative numbers can be simplified using [latex] \sqrt{-1}=i[/latex] and [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex]. Complex numbers have the form [latex]a+bi[/latex], where [latex]a[/latex] and [latex]b[/latex] are real numbers and [latex]i[/latex] is the square root of [latex]−1[/latex]. All real numbers can be written as complex numbers by setting [latex]b=0[/latex]. Imaginary numbers have the form [latex]bi[/latex] and can also be written as complex numbers by setting [latex]a=0[/latex].Contribute!
Licenses & Attributions
CC licensed content, Original
- Write Number in the Form of Complex Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Simplify Square Roots to Imaginary Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
