The Elimination Method Without Multiplication
Learning Outcomes
- Use the elimination method without multiplication
- Express the solution of an inconsistent system of equations containing two variables
- Express the solution of a dependent system of equations containing two variables
[latex] \displaystyle \begin{array}{l}\,\,\,\,\,x-y=\,-6\\\underline{+\,x+y=\,\,\,8}\\\,2x+0\,=\,\,\,\,2\end{array}[/latex]
You have eliminated the y term, and this equation can be solved using the methods for solving equations with one variable. Let’s see how this system is solved using the elimination method.Example
Use elimination to solve the system.[latex]\begin{array}{r}x–y=−6\\x+y=\,\,\,\,8\end{array}[/latex]
Answer: Add the equations.
[latex] \displaystyle \begin{array}{r}x-y=\,\,-6\\+\underline{\,\,x+y=\,\,\,\,\,8}\\\,\,\,\,\,\,2x\,\,\,\,\,=\,\,\,\,\,\,2\end{array}[/latex]
Solve for [latex]x[/latex].[latex]\begin{array}{r}2x=2\\x=1\end{array}[/latex]
Substitute [latex]x=1[/latex] into one of the original equations and solve for [latex]y[/latex].[latex]\begin{array}{l}x+y=8\\1+y=8\\\,\,\,\,\,\,\,\,\,\,y=8–1\\\,\,\,\,\,\,\,\,\,\,y=7\end{array}[/latex]
Be sure to check your answer in both equations![latex]\begin{array}{r}x–y=−6\\1–7=−6\\−6=−6\\\text{TRUE}\\\\x+y=8\\1+7=8\\8=8\\\text{TRUE}\end{array}[/latex]
The answers check.Answer
The solution is [latex](1, 7)[/latex].Example
Solve the given system of equations by elimination.Answer: Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, [latex]–1[/latex], is the opposite of the coefficient of [latex]x[/latex] in the first equation, [latex]1[/latex]. As a result, we can simply add the two equations together to eliminate [latex]x[/latex].
[latex]\begin{array}{l}3y=2\hfill \\ \text{ }y=\dfrac{2}{3}\hfill \end{array}[/latex]
Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex][latex]\begin{array}{l}\text{ }-x+y=3\hfill \\ \text{ }-x+\dfrac{2}{3}=3\hfill \\ \text{ }-x=3-\dfrac{2}{3}\hfill \\ \text{ }-x=\dfrac{7}{3}\hfill \\ \text{ }\:\:\:\:\:x=-\dfrac{7}{3}\hfill \end{array}[/latex]
The solution to this system is [latex]\left(-\dfrac{7}{3},\dfrac{2}{3}\right)[/latex]. Check the solution in the first equation.[latex]\begin{array}{llll}\text{ }x+2y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }\left(-\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right)=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{7}{3}+\dfrac{4}{3}=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{3}{3}=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }-1=-1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex]
We gain an important perspective on systems of equations by looking at the graphical representation. In the graph below, you will see that the equations intersect at the solution. We do not need to ask whether there may be a second solution, because observing the graph confirms that the system has exactly one solution.
[latex] \displaystyle \begin{array}{l}\,\,\,\,2x+y=12\\\underline{-3x+y=\,\,\,2}\\-x+2y=14\end{array}[/latex]
But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation. This means multiply every term in one of the equations by [latex]-1[/latex], so that the sign of every terms is opposite.[latex]\begin{array}{l}\,\,\,\,2x+\,\,y\,=12\rightarrow2x+y=12\rightarrow2x+y=12\\−3x+\,\,y\,=2\rightarrow−\left(−3x+y\right)=−(2)\rightarrow3x–y=−2\\\,\,\,\,5x+0y=10\end{array}[/latex]
You have eliminated the y variable, and the problem can now be solved. The following video describes a similar problem where you can eliminate one variable by adding the two equations together. https://youtu.be/M4IEmwcqR3c Caution! When you add the opposite of one entire equation to another, make sure to change the sign of EVERY term on both sides of the equation. This is a very common mistake to make.
Caution! When you add the opposite of one entire equation to another, make sure to change the sign of EVERY term on both sides of the equation. This is a very common mistake to make.Example
Use elimination to solve the system.[latex]\begin{array}{r}2x+y=12\\−3x+y=2\,\,\,\end{array}[/latex]
Answer: You can eliminate the y-variable if you add the opposite of one of the equations to the other equation.
[latex]\begin{array}{r}2x+y=12\\−3x+y=2\,\,\,\end{array}[/latex]
Rewrite the second equation as its opposite. Add. Solve for [latex]x[/latex].[latex]\begin{array}{r}2x+y=12\,\\3x–y=−2\\5x=10\,\\x=2\,\,\,\,\end{array}[/latex]
Substitute [latex]y=2[/latex] into one of the original equations and solve for [latex]y[/latex].[latex]\begin{array}{r}2\left(2\right)+y=12\\4+y=12\\y=8\,\,\,\end{array}[/latex]
Be sure to check your answer in both equations![latex]\begin{array}{r}2x+y=12\\2\left(2\right)+8=12\\4+8=12\\12=12\\\text{TRUE}\\\\−3x+y=2\\−3\left(2\right)+8=2\\−6+8=2\\2=2\\\text{TRUE}\end{array}[/latex]
The answers check.Answer
The solution is [latex](2, 8)[/latex].Try It
[ohm_question]38342[/ohm_question]Example
Use elimination to solve the system.[latex]\begin{array}{r}−2x+3y=−1\\2x+5y=\,25\end{array}[/latex]
Answer: Notice the coefficients of each variable in each equation. If you add these two equations, the x term will be eliminated since [latex]−2x+2x=0[/latex].
[latex]\begin{array}{r}−2x+3y=−1\\2x+5y=\,25\end{array}[/latex]
Add and solve for [latex]y[/latex].[latex]\begin{array}{r}−2x+3y=−1\\2x+5y=25\,\\8y=24\,\\y=3\,\,\,\,\end{array}[/latex]
Substitute [latex]y=3[/latex] into one of the original equations.[latex]\begin{array}{r}2x+5y=25\\2x+5\left(3\right)=25\\2x+15=25\\2x=10\\x=5\,\,\,\end{array}[/latex]
Check solutions.[latex]\begin{array}{r}−2x+3y=−1\\−2\left(5\right)+3\left(3\right)=−1\\−10+9=−1\\−1=−1\\\text{TRUE}\\\\2x+5y=25\\2\left(5\right)+5\left(3\right)=25\\10+15=25\\25=25\\\text{TRUE}\end{array}[/latex]
The answers check.Answer
The solution is [latex](5, 3)[/latex].Example
Use elimination to solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{r}4x+2y=14\\5x+2y=16\end{array}[/latex]
Answer: Notice the coefficients of each variable in each equation. You will need to add the opposite of one of the equations to eliminate the variable y, as [latex]2y+2y=4y[/latex], but [latex]2y+\left(−2y\right)=0[/latex].
[latex]\begin{array}{r}4x+2y=14\\5x+2y=16\end{array}[/latex]
Change one of the equations to its opposite, add and solve for [latex]x[/latex].[latex]\begin{array}{r}4x+2y=14\,\,\,\,\\−5x–2y=−16\\−x=−2\,\,\,\\x=2\,\,\,\,\,\,\,\end{array}[/latex]
Substitute [latex]x=2[/latex] into one of the original equations and solve for [latex]y[/latex].[latex]\begin{array}{r}4x+2y=14\\4\left(2\right)+2y=14\\8+2y=14\\2y=6\,\,\,\\y=3\,\,\,\end{array}[/latex]
Answer
The solution is [latex](2, 3)[/latex].Recognize systems that have no solution or an infinite number of solutions
Just as with the substitution method, the elimination method will sometimes eliminate both variables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution. Let’s look at an example.Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{r}-x–y=-4\\x+y=2\,\,\,\,\end{array}[/latex]
Answer: Add the equations to eliminate the [latex]x[/latex]-term.
[latex]\begin{array}{r}-x–y=-4\\\underline{x+y=2\,\,\,}\\0=−2\end{array}[/latex]
Answer
There is no solution.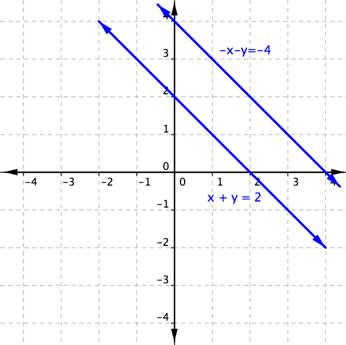
Try It
[ohm_question]115196[/ohm_question]Example
Solve for [latex]x[/latex] and [latex]y[/latex].[latex]\begin{array}{r}x+y=2\,\,\,\,\\-x−y=-2\end{array}[/latex]
Answer: Add the equations to eliminate the x-term.
[latex]\begin{array}{r}x+y=2\,\,\,\,\\\underline{-x−y=-2}\\0=0\,\,\,\,\,\end{array}[/latex]
Answer
There are an infinite number of solutions.
Try It
[ohm_question]115192[/ohm_question]Summary
Combining equations is a powerful tool for solving a system of equations. Adding or subtracting two equations in order to eliminate a common variable is called the elimination (or addition) method. Once one variable is eliminated, it becomes much easier to solve for the other one.Contribute!
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 1: Solve a System of Equations Using the Elimination Method . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex: System of Equations Using Elimination (Infinite Solutions) . Authored by: mathispower4u. License: All Rights Reserved. License terms: Standard YouTube License.
- Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
