Quadratic Equations
Learning Outcomes
- Recognize a quadratic equation
- Use the zero product principle to solve a quadratic equation that can be factored
Quadratic Equation
A quadratic equation is an equation containing a second-degree polynomial; for example,Principle of Zero Products
The Principle of Zero Products states that if the product of two numbers is [latex]0[/latex], then at least one of the factors is [latex]0[/latex]. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are [latex]0[/latex].How to solve a quadratic equation using factoring
- Make sure your quadratic equation is written in standard form, that is, [latex]a{x}^{2}+bx+c=0[/latex] where a, b, and c are real numbers, and [latex]a\ne 0[/latex].
- Factor the quadratic expression on the left-hand side of the equation.
- Solve using the zero-product property by setting each factor equal to zero and solving for the variable.
Example
Solve: [latex-display]-t^2+t=0[/latex-display]Answer: Each term has a common factor of [latex]t[/latex], so we can factor and use the zero product principle. Rewrite each term as the product of the GCF and the remaining terms. [latex-display]\begin{array}{c}-t^2=t\left(-t\right)\\t=t\left(1\right)\end{array}[/latex-display] Rewrite the polynomial equation using the factored terms in place of the original terms.
[latex]\begin{array}{c}-t^2+t=0\\t\left(-t\right)+t\left(1\right)\\t\left(-t+1\right)=0\end{array}[/latex]
Now we have a product on one side and zero on the other, so we can set each factor equal to zero using the zero product principle.
[latex]\begin{array}{c}t=0\,\,\,\,\,\,\,\,\text{ OR }\,\,\,\,\,\,\,\,\,\,\,-t+1=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-1}\,\,\,\underline{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-t=-1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-t}{-1}=\frac{-1}{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=1\end{array}[/latex]
Therefore, [latex]t=0\text{ OR }t=1[/latex].Example
Factor and solve the equation: [latex]{x}^{2}+x - 6=0[/latex].Answer: This equation is already in standard form, so we will proceed with factoring the left side of the equation. To factor [latex]{x}^{2}+x - 6=0[/latex], we look for two numbers whose product equals [latex]-6[/latex] and whose sum equals [latex]1[/latex]. Begin by looking at the possible factors of [latex]-6[/latex].
 In the following video, we provide more examples of factoring to solve quadratic equations where the leading coefficient is equal to 1.
https://youtu.be/bi7i_RuIGl0
In the following video, we provide more examples of factoring to solve quadratic equations where the leading coefficient is equal to 1.
https://youtu.be/bi7i_RuIGl0
Try It
[ohm_question]197328[/ohm_question]Example
Solve: [latex]s^2-4s=5[/latex]Answer: First, move all the terms to one side. The goal is to try and see if we can use the zero product principle since that is the only tool we know for solving polynomial equations.
[latex]\begin{array}{c}\,\,\,\,\,\,\,s^2-4s=5\\\,\,\,\,\,\,\,s^2-4s-5=0\\\end{array}[/latex]
We now have all the terms on the left side and zero on the other side. The polynomial [latex]s^2-4s-5[/latex] factors nicely which makes this equation a good candidate for the zero product principle.
[latex]\begin{array}{c}s^2-4s-5=0\\\left(s+1\right)\left(s-5\right)=0\end{array}[/latex]
We separate our factors into two linear equations using the principle of zero products.
[latex-display]\begin{array}{c}\left(s-5\right)=0\\s-5=0\\\,\,\,\,\,\,\,\,\,s=5\end{array}[/latex-display] OR [latex-display]\begin{array}{c}\left(s+1\right)=0\\s+1=0\\s=-1\end{array}[/latex-display] Therefore, [latex]s=-1\text{ OR }s=5[/latex].Example
Solve the quadratic equation: [latex]4{x}^{2}+15x+9=0[/latex].Answer: We can see that this equation is already in standard for, so we will proceed with factoring. Because this equation has a leading coefficient not equal to 1, we will factor by grouping: multiply [latex]ac:4\left(9\right)=36[/latex]. Then list the factors of [latex]36[/latex].
[latex]\begin{array}{lll}&\left(4x+3\right)\left(x+3\right)=0 & \hfill \\ \left(4x+3\right)\hfill=0 & & \left(x+3\right)=0 \hfill \\ x=-\frac{3}{4} & & x=-3 \hfill \end{array}[/latex]
The solutions are [latex]x=-\frac{3}{4}[/latex], [latex]x=-3[/latex].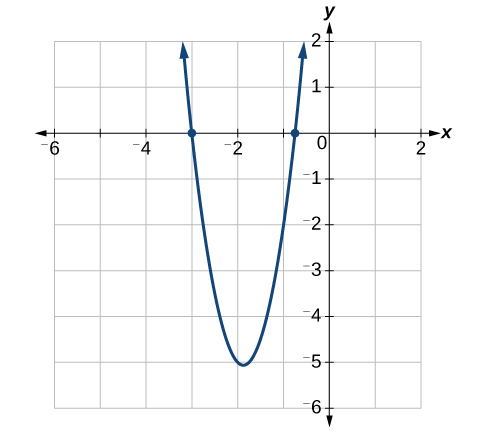 Notice that when we graph the equation [latex]y=4{x}^{2}+15x+9[/latex] we can see that the x-intercepts are [latex](-3,0)[/latex] and [latex](-\frac{3}{4},0)[/latex]. This agrees with our solutions!
Notice that when we graph the equation [latex]y=4{x}^{2}+15x+9[/latex] we can see that the x-intercepts are [latex](-3,0)[/latex] and [latex](-\frac{3}{4},0)[/latex]. This agrees with our solutions!
Example
Solve [latex]5b^{2}+4=−12b[/latex] for b.Answer: The original equation has [latex]−12b[/latex] on the right. To make this side equal to 0, add [latex]12b[/latex] to both sides.
[latex]5b^{2}+4+12b=−12b+12b[/latex]
Combine like terms.[latex]5b^{2}+12b+4=0[/latex]
Rewrite [latex]12b[/latex] as [latex]10b+2b[/latex].[latex]5b^{2}+10b+2b+4=0[/latex]
Factor out [latex]5b[/latex] from the first pair and 2 from the second pair.[latex]5b\left(b+2\right)+2\left(b+2\right)=0[/latex]
Factor out [latex]b+2[/latex].[latex]\left(5b+2\right)\left(b+2\right)=0[/latex]
Apply the Zero Product Property.[latex]5b+2=0\,\,\,\text{or}\,\,\,b+2=0[/latex]
Solve each equation.[latex]b=-\frac{2}{5}\,\,\,\text{OR}\,\,\,b=−2[/latex]
Answer
[latex-display]b=-\frac{2}{5}\,\,\,\text{or}\,\,\,b=−2[/latex-display]Example
Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]Answer: We can solve this in one of two ways. One way is to eliminate the fractions like you may have done when solving linear equations, and the second is to find a common denominator and factor fractions. Eliminating fractions is easier, so we will show that way. Start by multiplying the whole equation by [latex]2[/latex] to eliminate fractions:
[latex]\begin{array}{ccc}2\left(y^2-5=-\frac{7}{2}y+\frac{5}{2}\right)\\\,\,\,\,\,\,2(y^2)+2(-5)=2\left(-\frac{7}{2}y\right)+2\left(\frac{5}{2}\right)\\2y^2-10=-7y+5\end{array}[/latex]
Now we can move all the terms to one side and see if this will factor so we can use the principle of zero products.[latex]\begin{array}{c}2y^2-10=-7y+5\\2y^2-10+7y-5=0\\2y^2-15+7y=0\\2y^2+7y-15=0\end{array}[/latex]
We can now check whether this polynomial will factor. Using a table we can list factors until we find two numbers with a product of [latex]2\cdot-15=-30[/latex] and a sum of 7.| Factors of [latex]2\cdot-15=-30[/latex] | Sum of Factors |
|---|---|
| [latex]1,-30[/latex] | [latex]-29[/latex] |
| [latex]-1,30[/latex] | [latex]29[/latex] |
| [latex]2,-15[/latex] | [latex]-13[/latex] |
| [latex]-2,15[/latex] | [latex]13[/latex] |
| [latex]3,-10[/latex] | [latex]-7[/latex] |
| [latex]-3,10[/latex] | [latex]7[/latex] |
Therefore, [latex]y=\frac{3}{2}\text{ OR }y=-5[/latex].
Example
Solve for k: [latex]-2k^2+90=-8k[/latex]Answer: We need to move all the terms to one side so we can use the zero product principle.
[latex]\begin{array}{l}-2k^2+90=-8k\\\underline{+8k}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+8k}\\-2k^2+8k+90=0\end{array}[/latex]
You will either need to try to factor out a [latex]-2[/latex], or use the method where we multiply [latex]-2\cdot{90}[/latex] and find factors that sum to [latex]8[/latex]. Each term is divisible by [latex]2[/latex], so we can factor out [latex]-2[/latex].[latex]-2\left(k^2-4k-45\right)=0[/latex]
Note how we changed the signs when we factored out a negative number. If we can factor the polynomial, we will be able to solve. Using the shortcut for factoring we will start with the variable and place a plus and a minus sign in the binomials. We do this because [latex]45[/latex] is negative and the only way to get a product that is negative is if one of the factors is negative.[latex]-2\left(k-\,\,\,\right)\left(k+\,\,\,\right)=0[/latex]
We want our factors to have a product of [latex]-45[/latex] and a sum of [latex]-4[/latex]:
| Factors whose product is -45 | Sum of the factors |
|---|---|
| [latex]1\cdot-45=-45[/latex] | [latex]1-45=-44[/latex] |
| [latex]3\cdot-15=-45[/latex] | [latex]3-15=-12[/latex] |
| [latex]5\cdot-9=-45[/latex] | [latex]5-9=-4[/latex] |
[latex]-2\left(k-9\right)\left(k+5\right)=0[/latex]
Now we can set each factor equal to zero using the zero product rule.
[latex]-2=0[/latex] This solution is nonsense so we discard it.
[latex]k-9=0, k=9[/latex]
[latex]k+5=0, k=-5[/latex]
Answers
[latex-display]k=9\text{ and }k=-5[/latex-display]Example
Solve the difference of squares equation using the zero-product property: [latex]{x}^{2}-9=0[/latex].Answer: Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property. [latex-display]\begin{array}{lll}& {x}^{2}-9=0 & \hfill \\ \left(x - 3\right)\hfill=0 & & \left(x+3\right)=0 \hfill \\ x=3 & & x=-3 \hfill \end{array}[/latex-display] The solutions are [latex]x=3[/latex] and [latex]x=-3[/latex].
Example
Solve the equation by factoring: [latex]-3{x}^{3}-5{x}^{2}-2x=0[/latex].Answer: This equation does not look like a quadratic, as the highest power is [latex]3[/latex], not [latex]2[/latex]. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out [latex]-x[/latex] from all of the terms and then proceed with grouping.
[latex]\begin{array}{ccc}-x=0&\left(3x+2\right)=0&\left(x+1\right)=0 \hfill \\ x=0 & x=-\frac{2}{3} & x=-1 \hfill \end{array}[/latex]
The solutions are [latex]x=0[/latex], [latex]x=-\frac{2}{3}[/latex], and [latex]x=-1[/latex].Summary
You can find the solutions, or roots, of quadratic equations by setting one side equal to zero, factoring the polynomial, and then applying the Zero Product Property. The Principle of Zero Products states that if [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are [latex]0[/latex]. Once the polynomial is factored, set each factor equal to zero and solve them separately. The answers will be the set of solutions for the original equation.Contribute!
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Quadratic Equation App - Find the Dimensions of a Rectangle Given Area (Factoring). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve a Quadratic Equation Using Factor By Grouping. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Factor and Solve Quadratic Equation - Trinomial a = -1. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
