We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > ALGEBRA / TRIG I

Finding All the Factors of a Number

Learning Outcomes

  • Find all the factors of a number
  • Determine whether a number is prime or composite
There are often several ways to talk about the same idea. So far, we’ve seen that if [latex]m[/latex] is a multiple of [latex]n[/latex], we can say that [latex]m[/latex] is divisible by [latex]n[/latex]. We know that [latex]72[/latex] is the product of [latex]8[/latex] and [latex]9[/latex], so we can say [latex]72[/latex] is a multiple of [latex]8[/latex] and [latex]72[/latex] is a multiple of [latex]9[/latex]. We can also say [latex]72[/latex] is divisible by [latex]8[/latex] and by [latex]9[/latex]. Another way to talk about this is to say that [latex]8[/latex] and [latex]9[/latex] are factors of [latex]72[/latex]. When we write [latex]72=8\cdot 9[/latex] we can say that we have factored [latex]72[/latex]. The image shows the equation 8 times 9 equals 72. The 8 and 9 are labeled as factors and the 72 is labeled product.

Factors

If [latex]a\cdot b=m[/latex], then [latex]a\text{ and }b[/latex] are factors of [latex]m[/latex], and [latex]m[/latex] is the product of [latex]a\text{ and }b[/latex].
In algebra, it can be useful to determine all of the factors of a number. This is called factoring a number, and it can help us solve many kinds of problems. For example, suppose a choreographer is planning a dance for a ballet recital. There are [latex]24[/latex] dancers, and for a certain scene, the choreographer wants to arrange the dancers in groups of equal sizes on stage. In how many ways can the dancers be put into groups of equal size? Answering this question is the same as identifying the factors of [latex]24[/latex]. The table below summarizes the different ways that the choreographer can arrange the dancers.
Number of Groups Dancers per Group Total Dancers
[latex]1[/latex] [latex]24[/latex] [latex]1\cdot 24=24[/latex]
[latex]2[/latex] [latex]12[/latex] [latex]2\cdot 12=24[/latex]
[latex]3[/latex] [latex]8[/latex] [latex]3\cdot 8=24[/latex]
[latex]4[/latex] [latex]6[/latex] [latex]4\cdot 6=24[/latex]
[latex]6[/latex] [latex]4[/latex] [latex]6\cdot 4=24[/latex]
[latex]8[/latex] [latex]3[/latex] [latex]8\cdot 3=24[/latex]
[latex]12[/latex] [latex]2[/latex] [latex]12\cdot 2=24[/latex]
[latex]24[/latex] [latex]1[/latex] [latex]24\cdot 1=24[/latex]
What patterns do you see in the table above? Did you notice that the number of groups times the number of dancers per group is always [latex]24?[/latex] This makes sense, since there are always [latex]24[/latex] dancers. You may notice another pattern if you look carefully at the first two columns. These two columns contain the exact same set of numbers—but in reverse order. They are mirrors of one another, and in fact, both columns list all of the factors of [latex]24[/latex], which are:

[latex]1,2,3,4,6,8,12,24[/latex]

We can find all the factors of any counting number by systematically dividing the number by each counting number, starting with [latex]1[/latex]. If the quotient is also a counting number, then the divisor and the quotient are factors of the number. We can stop when the quotient becomes smaller than the divisor.

Find all the factors of a counting number

  1. Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
    • If the quotient is a counting number, the divisor and quotient are a pair of factors.
    • If the quotient is not a counting number, the divisor is not a factor.
  2. List all the factor pairs.
  3. Write all the factors in order from smallest to largest.
 

example

Find all the factors of [latex]72[/latex]. Solution: Divide [latex]72[/latex] by each of the counting numbers starting with [latex]1[/latex]. If the quotient is a whole number, the divisor and quotient are a pair of factors. The figure shows a table with ten rows and four columns. The first row is a header row and labels the rows The next line would have a divisor of [latex]9[/latex] and a quotient of [latex]8[/latex]. The quotient would be smaller than the divisor, so we stop. If we continued, we would end up only listing the same factors again in reverse order. Listing all the factors from smallest to greatest, we have [latex]1,2,3,4,6,8,9,12,18,24,36,\text{ and }72[/latex]
  In the following video we show how to find all the factors of [latex]30[/latex]. https://youtu.be/3EL3VA2v9iI

Identify Prime and Composite Numbers

Some numbers, like [latex]72[/latex], have many factors. Other numbers, such as [latex]7[/latex], have only two factors: [latex]1[/latex] and the number. A number with only two factors is called a prime number. A number with more than two factors is called a composite number. The number [latex]1[/latex] is neither prime nor composite. It has only one factor, itself.

Prime Numbers and Composite Numbers

A prime number is a counting number greater than [latex]1[/latex] whose only factors are [latex]1[/latex] and itself. A composite number is a counting number that is not prime.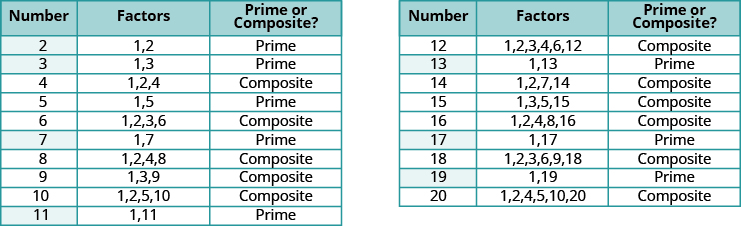
The table below lists the counting numbers from [latex]2[/latex] through [latex]20[/latex] along with their factors. The highlighted numbers are prime, since each has only two factors. Factors of the counting numbers from [latex]2[/latex] through [latex]20[/latex], with prime numbers highlighted This figure shows a table with twenty rows and three columns. The first row is a header row. It labels the columns as The prime numbers less than [latex]20[/latex] are [latex]2,3,5,7,11,13,17,\text{and }19[/latex]. There are many larger prime numbers too. In order to determine whether a number is prime or composite, we need to see if the number has any factors other than [latex]1[/latex] and itself. To do this, we can test each of the smaller prime numbers in order to see if it is a factor of the number. If none of the prime numbers are factors, then that number is also prime.

Determine if a number is prime

  1. Test each of the primes, in order, to see if it is a factor of the number.
  2. Start with [latex]2[/latex] and stop when the quotient is smaller than the divisor or when a prime factor is found.
  3. If the number has a prime factor, then it is a composite number. If it has no prime factors, then the number is prime.
 

example

Identify each number as prime or composite:
  1. [latex]83[/latex]
  2. [latex]77[/latex]

Answer: Solution: 1. Test each prime, in order, to see if it is a factor of [latex]83[/latex] , starting with [latex]2[/latex], as shown. We will stop when the quotient is smaller than the divisor.

Prime Test Factor of [latex]83?[/latex]
[latex]2[/latex] Last digit of [latex]83[/latex] is not [latex]0,2,4,6,\text{or }8[/latex]. No.
[latex]3[/latex] [latex]8+3=11[/latex], and [latex]11[/latex] is not divisible by [latex]3[/latex]. No.
[latex]5[/latex] The last digit of [latex]83[/latex] is not [latex]5[/latex] or [latex]0[/latex]. No.
[latex]7[/latex] [latex]83\div 7=(11.857\dots)[/latex] No.
[latex]11[/latex] [latex]83\div 11=(7.545\dots)[/latex] No.
We can stop when we get to [latex]11[/latex] because the quotient [latex](7.545\dots)[/latex] is less than the divisor. We did not find any prime numbers that are factors of [latex]83[/latex], so we know [latex]83[/latex] is prime. 2. Test each prime, in order, to see if it is a factor of [latex]77[/latex].
Prime Test Factor of [latex]77?[/latex]
[latex]2[/latex] Last digit is not [latex]0,2,4,6,\text{or }8[/latex]. No.
[latex]3[/latex] [latex]7+7=14[/latex], and [latex]14[/latex] is not divisible by [latex]3[/latex]. No.
[latex]5[/latex] the last digit is not [latex]5[/latex] or [latex]0[/latex]. No.
[latex]7[/latex] [latex]77\div 11=7[/latex] Yes.
Since [latex]77[/latex] is divisible by [latex]7[/latex], we know it is not a prime number. It is composite.

 

try it

[ohm_question]145441[/ohm_question]
In the following video we show more examples of how to determine whether a number is prime or composite. https://youtu.be/8v7baCT33xw

Contribute!

Did you have an idea for improving this content? We’d love your input.

Licenses & Attributions

CC licensed content, Original

  • Question ID 145441, 145439. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License.

CC licensed content, Shared previously

  • Ex 1: Determine Factors of a Number. License: CC BY: Attribution.
  • Ex 1: Prime Factorization Using Stacked Division. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Determine if Numbers Are Prime or Composite (Algorithm). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Specific attribution