Using the Slope Formula to Find the Slope between Two Points
Learning Outcomes
- Use the slope formula to find the slope of a line between two points
- Find the slope of horizontal and vertical lines
The Slope Formula
You’ve seen that you can find the slope of a line on a graph by measuring the rise and the run. You can also find the slope of a straight line without its graph if you know the coordinates of any two points on that line. Every point has a set of coordinates: an [latex]x[/latex]-value and a [latex]y[/latex]-value, written as an ordered pair [latex](x, y)[/latex]. The [latex]x[/latex] value tells you where a point is horizontally. The [latex]y[/latex] value tells you where the point is vertically. Consider two points on a line—Point 1 and Point 2. Point 1 has coordinates [latex]\left(x_{1},y_{1}\right)[/latex] and Point 2 has coordinates [latex]\left(x_{2},y_{2}\right)[/latex]. The rise is the vertical distance between the two points, which is the difference between their [latex]y[/latex]-coordinates. That makes the rise [latex]\left(y_{2}-y_{1}\right)[/latex]. The run between these two points is the difference in the [latex]x[/latex]-coordinates, or [latex]\left(x_{2}-x_{1}\right)[/latex].
So, [latex] \displaystyle \text{Slope}=\frac{\text{rise}}{\text{run}}[/latex] or [latex] \displaystyle m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}[/latex].
To see how the rise and run relate to the coordinates of the two points, let’s take another look at the slope of the line between the points [latex]\left(2,3\right)[/latex] and [latex]\left(7,6\right)[/latex] below.
The rise is the vertical distance between the two points, which is the difference between their [latex]y[/latex]-coordinates. That makes the rise [latex]\left(y_{2}-y_{1}\right)[/latex]. The run between these two points is the difference in the [latex]x[/latex]-coordinates, or [latex]\left(x_{2}-x_{1}\right)[/latex].
So, [latex] \displaystyle \text{Slope}=\frac{\text{rise}}{\text{run}}[/latex] or [latex] \displaystyle m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}[/latex].
To see how the rise and run relate to the coordinates of the two points, let’s take another look at the slope of the line between the points [latex]\left(2,3\right)[/latex] and [latex]\left(7,6\right)[/latex] below.
 Since we have two points, we will use subscript notation.
Since we have two points, we will use subscript notation.
[latex]\stackrel{{x}_{1},{y}_{1}}{\left(2,3\right)}\stackrel{{x}_{2},{y}_{2}}{\left(7,6\right)}[/latex]
On the graph, we counted the rise of [latex]3[/latex]. The rise can also be found by subtracting the [latex]y\text{-coordinates}[/latex] of the points.[latex]\begin{array}{c}{y}_{2}-{y}_{1}\\ 6 - 3\\ 3\end{array}[/latex]
We counted a run of [latex]5[/latex]. The run can also be found by subtracting the [latex]x\text{-coordinates}[/latex].[latex]\begin{array}{c}{x}_{2}-{x}_{1}\\ 7 - 2\\ 5\end{array}[/latex]
| We know | [latex]m={\Large\frac{\text{rise}}{\text{run}}}[/latex] |
| So | [latex]m={\Large\frac{3}{5}}[/latex] |
| We rewrite the rise and run by putting in the coordinates. | [latex]m={\Large\frac{6 - 3}{7 - 2}}[/latex] |
| But [latex]6[/latex] is the [latex]y[/latex] -coordinate of the second point, [latex]{y}_{2}[/latex] and [latex]3[/latex] is the [latex]y[/latex] -coordinate of the first point [latex]{y}_{1}[/latex] . So we can rewrite the rise using subscript notation. | [latex]m={\Large\frac{{y}_{2}-{y}_{1}}{7 - 2}}[/latex] |
| Also [latex]7[/latex] is the [latex]x[/latex] -coordinate of the second point, [latex]{x}_{2}[/latex] and [latex]2[/latex] is the [latex]x[/latex] -coordinate of the first point [latex]{x}_{2}[/latex] . So we rewrite the run using subscript notation. | [latex]m={\Large\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}[/latex] |
Slope Formula
The slope of the line between two points [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex] is [latex-display]m={\Large\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}[/latex-display] Say the formula to yourself to help you remember it:[latex]\text{Slope is }y\text{ of the second point minus }y\text{ of the first point}[/latex] [latex-display]\text{over}[/latex-display] [latex]x\text{ of the second point minus }x\text{ of the first point.}[/latex]
example
Find the slope of the line between the points [latex]\left(1,2\right)[/latex] and [latex]\left(4,5\right)[/latex]. Solution| We’ll call [latex]\left(1,2\right)[/latex] point #1 and [latex]\left(4,5\right)[/latex] point #2. | [latex]\stackrel{{x}_{1},{y}_{1}}{\left(1,2\right)}\text{and}\stackrel{{x}_{2},{y}_{2}}{\left(4,5\right)}[/latex] |
| Use the slope formula. | [latex]m={\Large\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}[/latex] |
| Substitute the values in the slope formula: | |
| [latex]y[/latex] of the second point minus [latex]y[/latex] of the first point | [latex]m={\Large\frac{5 - 2}{{x}_{2}-{x}_{1}}}[/latex] |
| [latex]x[/latex] of the second point minus [latex]x[/latex] of the first point | [latex]m={\Large\frac{5 - 2}{4 - 1}}[/latex] |
| Simplify the numerator and the denominator. | [latex]m={\Large\frac{3}{3}}[/latex] |
| [latex]m=1[/latex] |
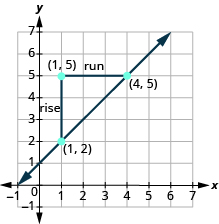 The rise is [latex]3[/latex] and the run is [latex]3[/latex], so
[latex-display]\begin{array}{}\\ m=\frac{\text{rise}}{\text{run}}\hfill \\ m={\Large\frac{3}{3}}\hfill \\ m=1\hfill \end{array}[/latex-display]
The rise is [latex]3[/latex] and the run is [latex]3[/latex], so
[latex-display]\begin{array}{}\\ m=\frac{\text{rise}}{\text{run}}\hfill \\ m={\Large\frac{3}{3}}\hfill \\ m=1\hfill \end{array}[/latex-display]
 You can see from the graph that the rise going from Point 1 to Point 2 is [latex]4[/latex], because you are moving [latex]4[/latex] units in a positive direction (up). The run is [latex]−2[/latex], because you are then moving in a negative direction (left) [latex]2[/latex] units (think of it like running backwards!). Using the slope formula,
You can see from the graph that the rise going from Point 1 to Point 2 is [latex]4[/latex], because you are moving [latex]4[/latex] units in a positive direction (up). The run is [latex]−2[/latex], because you are then moving in a negative direction (left) [latex]2[/latex] units (think of it like running backwards!). Using the slope formula,
[latex] \displaystyle \text{Slope}=\frac{\text{rise}}{\text{run}}=\frac{4}{-2}=-2[/latex].
You do not need the graph to find the slope. You can just use the coordinates, keeping careful track of which is Point 1 and which is Point 2. Let’s organize the information about the two points:| Name | Ordered Pair | Coordinates |
|---|---|---|
| Point 1 | [latex](0,2)[/latex] | [latex]\begin{array}{l}x_{1}=0\\y_{1}=2\end{array}[/latex] |
| Point 2 | [latex](−2,6)[/latex] | [latex]\begin{array}{l}x_{2}=-2\\y_{2}=6\end{array}[/latex] |
try it
[ohm_question]147021[/ohm_question]example
Find the slope of the line through the points [latex]\left(-2,-3\right)[/latex] and [latex]\left(-7,4\right)[/latex].Answer: Solution
| We’ll call [latex]\left(-2,-3\right)[/latex] point #1 and [latex]\left(-7,4\right)[/latex] point #2. | [latex]\stackrel{{x}_{1},{y}_{1}}{\left(-2,-3\right)}\text{and}\stackrel{{x}_{2},{y}_{2}}{\left(-7,4\right)}[/latex] |
| Use the slope formula. | [latex]m={\Large\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}[/latex] |
| Substitute the values | |
| [latex]y[/latex] of the second point minus [latex]y[/latex] of the first point | [latex]m={\Large\frac{4-\left(-3\right)}{{x}_{2}-{x}_{1}}}[/latex] |
| [latex]x[/latex] of the second point minus [latex]x[/latex] of the first point | [latex]m={\Large\frac{4-\left(-3\right)}{-7-\left(-2\right)}}[/latex] |
| Simplify. | [latex]m={\Large\frac{7}{-5}}[/latex] |
| [latex]m=-{\Large\frac{7}{5}}[/latex] |
 [latex-display]\begin{array}{}\\ \\ \\ m=\frac{\text{rise}}{\text{run}}\\ m={\Large\frac{-7}{5}}\\ m=-{\Large\frac{7}{5}}\end{array}[/latex-display]
[latex-display]\begin{array}{}\\ \\ \\ m=\frac{\text{rise}}{\text{run}}\\ m={\Large\frac{-7}{5}}\\ m=-{\Large\frac{7}{5}}\end{array}[/latex-display]
try it
[ohm_question]147022[/ohm_question]Example
What is the slope of the line that contains the points [latex](4,2)[/latex] and [latex](5,5)[/latex]?Answer:
| [latex]\begin{array}{l}x_{1}=4\\y_{1}=2\end{array}[/latex] | [latex]\left(4,2\right)=\text{Point }1,\left(x_{1},y_{1}\right)[/latex] |
| [latex]\begin{array}{l}x_{2}=5\\y_{2}=5\end{array}[/latex] | [latex]\left(5,5\right)=\text{Point }2,\left(x_{2},y_{2}\right)[/latex] |
| [latex]\begin{array}{l}m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-2}{5-4}=\frac{3}{1}\\\\m=3\end{array}[/latex] | Substitute the values into the slope formula and simplify. |
Answer
The slope is [latex]3[/latex].Example
What is the slope of the line that contains the points [latex](5,5)[/latex] and [latex](4,2)[/latex]?Answer:
| [latex]\begin{array}{l}x_{1}=5\\y_{1}=5\end{array}[/latex] | [latex](5,5)=\text{Point }1[/latex], [latex]\left(x_{1},y_{1}\right)[/latex] |
| [latex]\begin{array}{l}x_{2}=4\\y_{2}=2\end{array}[/latex] | [latex](4,2)=\text{Point }2[/latex], [latex]\left(x_{2},y_{2}\right)[/latex] |
| [latex]\begin{array}{l}m=\frac{y_{2}-y_{1}}{{x_2}-x_{1}}\\\\m=\frac{2-5}{4-5}=\frac{-3}{-1}=3\\\\m=3\end{array}[/latex] | Substitute the values into the slope formula and simplify. |
Answer
The slope is [latex]3[/latex].Example (Advanced)
What is the slope of the line that contains the points [latex](3,-6.25)[/latex] and [latex](-1,8.5)[/latex]?Answer:
| [latex]\begin{array}{l}x_{1}=3\\y_{1}=-6.25\end{array}[/latex] | [latex](3,-6.25)=\text{Point }1[/latex], [latex] \displaystyle ({{x}_{1}},{{y}_{1}})[/latex] |
| [latex] \displaystyle \begin{array}{l}{{x}_{2}}=-1\\{{y}_{2}}=8.5\end{array}[/latex] | [latex](-1,8.5)=\text{Point }2[/latex], [latex] \displaystyle ({{x}_{2}},{{y}_{2}})[/latex] |
| [latex] \displaystyle \begin{array}{l}m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\\\\m=\frac{8.5-(-6.25)}{-1-3}\\\\m=\frac{14.75}{-4}\\\\m=-3.6875\end{array}[/latex] | Substitute the values into the slope formula and simplify. |
Answer
The slope is [latex]-3.6875[/latex]Finding the Slopes of Horizontal and Vertical Lines
Now, let's revisit horizontal and vertical lines. So far in this section, we have considered lines that run “uphill” or “downhill.” Their slopes are always positive or negative numbers. But what about horizontal and vertical lines? Can we still use the slope formula to calculate their slopes? Consider the line above. We learned in the previous section that because it is horizontal, its slope is [latex]0[/latex]. You can also use the slope formula with two points on this horizontal line to calculate the slope of this horizontal line. Using [latex](−3,3)[/latex] as Point 1 and (2, 3) as Point 2, you get:
Consider the line above. We learned in the previous section that because it is horizontal, its slope is [latex]0[/latex]. You can also use the slope formula with two points on this horizontal line to calculate the slope of this horizontal line. Using [latex](−3,3)[/latex] as Point 1 and (2, 3) as Point 2, you get:
[latex] \displaystyle \begin{array}{l}m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\\\\m=\frac{3-3}{2-\left(-3\right)}=\frac{0}{5}=0\end{array}[/latex]
The slope of this horizontal line is [latex]0[/latex]. Let’s consider any horizontal line. No matter which two points you choose on the line, they will always have the same y-coordinate. So, when you apply the slope formula, the numerator will always be [latex]0[/latex]. Zero divided by any non-zero number is [latex]0[/latex], so the slope of any horizontal line is always [latex]0[/latex]. The equation for the horizontal line [latex]y=3[/latex] is telling you that no matter which two points you choose on this line, the y-coordinate will always be [latex]3[/latex]. How about vertical lines? In their case, no matter which two points you choose, they will always have the same x-coordinate. The equation for this line is [latex]x=2[/latex]. So, what happens when you use the slope formula with two points on this vertical line to calculate the slope? Using [latex](2,1)[/latex] as Point 1 and [latex](2,3)[/latex] as Point 2, you get:
So, what happens when you use the slope formula with two points on this vertical line to calculate the slope? Using [latex](2,1)[/latex] as Point 1 and [latex](2,3)[/latex] as Point 2, you get:
[latex] \displaystyle \begin{array}{l}m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\\\\m=\frac{3-1}{2-2}=\frac{2}{0}\end{array}[/latex]
But division by zero has no meaning for the set of real numbers. Because of this fact, it is said that the slope of this vertical line is undefined. This is true for all vertical lines—they all have a slope that is undefined.Example
What is the slope of the line that contains the points [latex](3,2)[/latex] and [latex](−8,2)[/latex]?Answer:
| [latex] \displaystyle \begin{array}{l}{{x}_{1}}=3\\{{y}_{1}}=2\end{array}[/latex] | [latex](3,2)=\text{Point }1[/latex], [latex] \displaystyle \left(x_{1},x_{2}\right)[/latex] |
| [latex] \displaystyle \begin{array}{l}{{x}_{2}}=-8\\\\{{y}_{2}}=2\end{array}[/latex] | [latex](−8,2)=\text{Point }2[/latex], [latex] \displaystyle ({{x}_{2}},{{y}_{2}})[/latex] |
| [latex] \displaystyle \begin{array}{l}\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\\\\\frac{(2)-(2)}{(-8)-(3)}=\frac{0}{-11}=0\\\\m=0\end{array}[/latex] | Substitute the values into the slope formula and simplify. |
Answer
The slope is [latex]0[/latex], so the line is horizontal.Try It
[ohm_question]76720[/ohm_question] [ohm_question]195555[/ohm_question]Contribute!
Licenses & Attributions
CC licensed content, Original
- Question ID 147022, 147021, 147020. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Determine the Slope a Line Given Two Points on a Line. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
