Volume and Surface Area of a Sphere
For a sphere with radius [latex]r\text{:}[/latex]

example
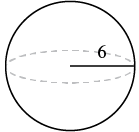
A sphere has a radius [latex]6[/latex] inches. Find 1. its volume and 2. its surface area.
Solution
Step 1 is the same for both 1. and 2., so we will show it just once.
| Step 1. Read the problem. Draw the figure and label
it with the given information. |
 |
| 1. |
|
| Step 2. Identify what you are looking for. |
The volume of the sphere |
| Step 3. Name. Choose a variable to represent it. |
Let [latex]V[/latex] = volume. |
| Step 4. Translate.
Write the appropriate formula. |
[latex]V=\Large\frac{4}{3}\normalsize\pi {r}^{3}[/latex] |
| Step 5. Solve. |
[latex]V\approx
\Large\frac{4}{3}\normalsize\left(3.14\right)({6}in)^{3}[/latex]
[latex]V\approx 904.32in^3[/latex] |
| Step 6. Check: Double-check your math on a calculator. |
|
| Step 7. Answer the question. |
The volume is approximately [latex]904.32[/latex] cubic inches. |
| 2. |
|
| Step 2. Identify what you are looking for. |
The surface area of the cube |
| Step 3. Name. Choose a variable to represent it. |
Let S = surface area. |
| Step 4. Translate.
Write the appropriate formula. |
[latex]S=4\pi {r}^{2}[/latex] |
| Step 5. Solve. |
[latex]S\approx 4\left(3.14\right)({6}in)^{2}[/latex]
[latex]S\approx 452.16in^2[/latex] |
| Step 6. Check: Double-check your math on a calculator |
|
| Step 7. Answer the question. |
The surface area is approximately [latex]452.16[/latex] square inches. |
example
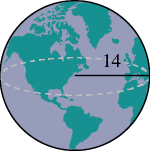
A globe of Earth is in the shape of a sphere with radius [latex]14[/latex] centimeters. Find 1. its volume and 2. its surface area. Round the answer to the nearest hundredth.
Answer:
Solution
| Step 1. Read the problem. Draw a figure with the
given information and label it. |
 |
| 1. |
|
| Step 2. Identify what you are looking for. |
The volume of the sphere |
| Step 3. Name. Choose a variable to represent it. |
Let [latex]V[/latex] = volume. |
| Step 4. Translate.
Write the appropriate formula.
Substitute. (Use 3.14 for [latex]\pi [/latex] ) |
[latex]V=\Large\frac{4}{3}\normalsize\pi {r}^{3}[/latex]
[latex]V\approx \Large\frac{4}{3}\normalsize\left(3.14\right)({14}cm)^{3}[/latex] |
| Step 5. Solve. |
[latex]V\approx 11,488.21cm^3[/latex] |
| Step 6. Check: We leave it to you to check your calculations. |
|
| Step 7. Answer the question. |
The volume is approximately [latex]11,488.21[/latex] cubic centimeters. |
| 2. |
|
| Step 2. Identify what you are looking for. |
The surface area of the sphere |
| Step 3. Name. Choose a variable to represent it. |
Let S = surface area. |
| Step 4. Translate.
Write the appropriate formula.
Substitute. (Use 3.14 for [latex]\pi [/latex] ) |
[latex]S=4\pi {r}^{2}[/latex]
[latex]S\approx 4\left(3.14\right)({14}cm)^{2}[/latex] |
| Step 5. Solve. |
[latex]S\approx 2461.76cm^2[/latex] |
| Step 6. Check: We leave it to you to check your calculations. |
|
| Step 7. Answer the question. |
The surface area is approximately [latex]2461.76[/latex] square centimeters. |
Did you have an idea for improving this content? We’d love your input.



