Identifying the Intercepts on the Graph of a Line
Learning Outcomes
- Identify the [latex]x[/latex] and [latex]y[/latex]-intercepts from the graph of a line
- Identify the [latex]x[/latex] and [latex]y[/latex]-intercepts from the equation of a line
Every linear equation has a unique line that represents all the solutions of the equation. When graphing a line by plotting points, each person who graphs the line can choose any three points, so two people graphing the line might use different sets of points.
At first glance, their two lines might appear different since they would have different points labeled. But if all the work was done correctly, the lines will be exactly the same line. One way to recognize that they are indeed the same line is to focus on where the line crosses the axes. Each of these points is called an intercept of the line.
The intercepts of a line are the points where the line intercepts, or crosses, the horizontal and vertical axes. To help you remember what “intercept” means, think about the word “intersect.” The two words sound alike and in this case mean the same thing.
Intercepts of a Line
Each of the points at which a line crosses the [latex]x\text{-axis}[/latex] and the [latex]y\text{-axis}[/latex] is called an intercept of the line.
Identify the [latex]x[/latex]- and [latex]y[/latex]- Intercepts From a Graph
The straight line on the graph below intercepts the two coordinate axes. The point where the line crosses the x-axis is called the [latex]x[/latex]-intercept. The [latex]y[/latex]-intercept is the point where the line crosses the y-axis.
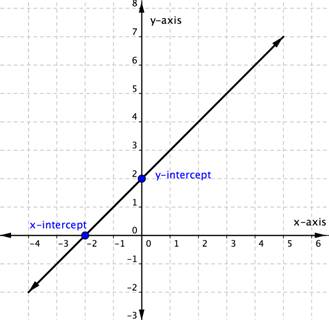 In the graph above, the x-intercept occurs when [latex]x=-2[/latex] and the y-intercept occurs when [latex]y=2[/latex]. We typically express the intercepts by giving the ordered pair, so we say that the x-intercept above is at the point [latex](−2,0)[/latex] and the y-intercept above is at the point [latex](0, 2)[/latex].
Notice that the intercept always occurs where [latex]x=0[/latex], and the x-intercept always occurs where [latex]y=0[/latex].
Let’s look at the graph of the lines shown below.
In the graph above, the x-intercept occurs when [latex]x=-2[/latex] and the y-intercept occurs when [latex]y=2[/latex]. We typically express the intercepts by giving the ordered pair, so we say that the x-intercept above is at the point [latex](−2,0)[/latex] and the y-intercept above is at the point [latex](0, 2)[/latex].
Notice that the intercept always occurs where [latex]x=0[/latex], and the x-intercept always occurs where [latex]y=0[/latex].
Let’s look at the graph of the lines shown below.
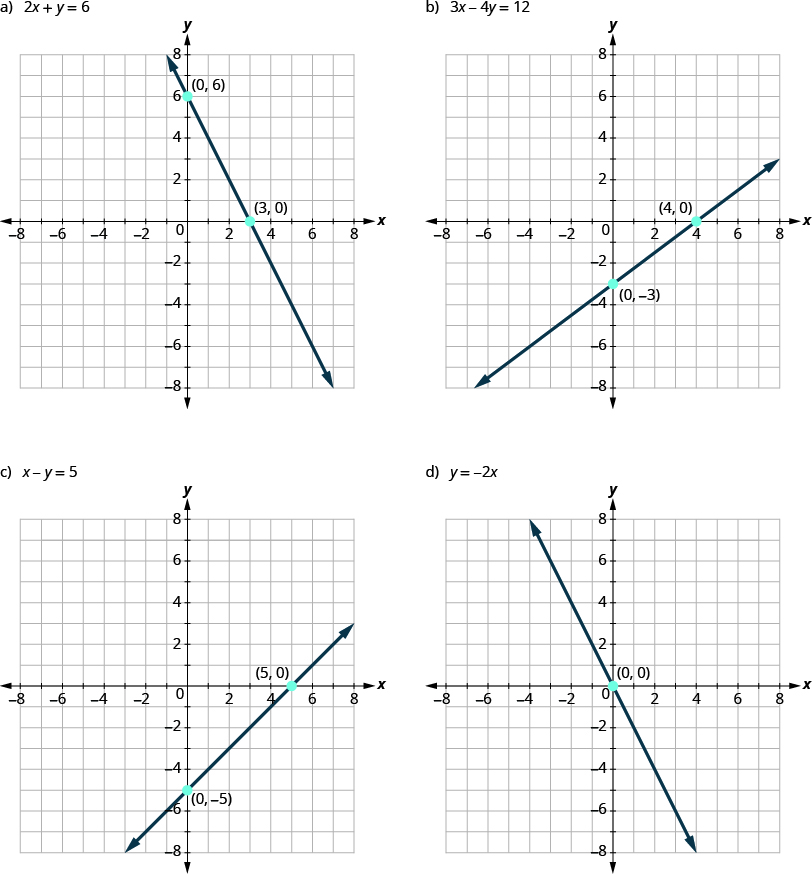 First, notice where each of these lines crosses the x- axis:
First, notice where each of these lines crosses the x- axis:
| Figure: |
The line crosses the x-axis at: |
Ordered pair of this point |
| [latex]a[/latex] |
[latex]3[/latex] |
[latex](3,0)[/latex] |
| [latex]b[/latex] |
[latex]4[/latex] |
[latex](4,0)[/latex] |
| [latex]c[/latex] |
[latex]5[/latex] |
[latex](5,0)[/latex] |
| [latex]d[/latex] |
[latex]0[/latex] |
[latex](0,0)[/latex] |
Do you see a pattern?
For each row, the y- coordinate of the point where the line crosses the x- axis is zero. The point where the line crosses the x- axis has the form [latex]\left(a,0\right)[/latex] ; and is called the x-intercept of the line. The x-intercept occurs when y is zero.
Now, let's look at the points where these lines cross the y-axis.
| Figure: |
The line crosses the y-axis at: |
Ordered pair for this point |
| [latex]a[/latex] |
[latex]6[/latex] |
[latex](0,6)[/latex] |
| [latex]b[/latex] |
[latex]-3[/latex] |
[latex](0,-3)[/latex] |
| [latex]c[/latex] |
[latex]-5[/latex] |
[latex](0,-5)[/latex] |
| [latex]d[/latex] |
[latex]0[/latex] |
[latex](0,0)[/latex] |
[latex]x[/latex]-intercept and [latex]y[/latex]-intercept of a line
The [latex]x\text{-intercept}[/latex] is the point, [latex]\left(a,0\right)[/latex], where the graph crosses the [latex]x\text{-axis}[/latex]. The [latex]x\text{-intercept}[/latex] occurs when [latex]\text{y}[/latex] is zero.
The [latex]y\text{-intercept}[/latex] is the point, [latex]\left(0,b\right)[/latex], where the graph crosses the [latex]y\text{-axis}[/latex]. The [latex]y\text{-intercept}[/latex] occurs when [latex]\text{x}[/latex] is zero.
example
Find the [latex]x\text{- and }y\text{-intercepts}[/latex] of each line:
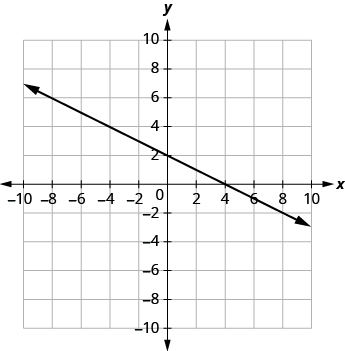
| 1. [latex]x+2y=4[/latex] |
 |
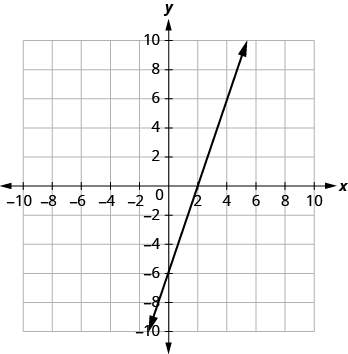
| 2. [latex]3x-y=6[/latex] |
 |
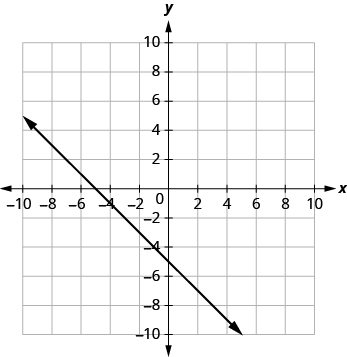
| 3. [latex]x+y=-5[/latex] |
 |
Solution
| 1. |
|
| The graph crosses the x-axis at the point [latex](4, 0)[/latex]. |
The x-intercept is [latex](4, 0)[/latex]. |
| The graph crosses the y-axis at the point [latex](0, 2)[/latex]. |
The y-intercept is [latex](0, 2)[/latex]. |
| 2. |
|
| The graph crosses the x-axis at the point [latex](2, 0)[/latex]. |
The x-intercept is [latex](2, 0)[/latex] |
| The graph crosses the y-axis at the point [latex](0, −6)[/latex]. |
The y-intercept is [latex](0, −6)[/latex]. |
| 3. |
|
| The graph crosses the x-axis at the point [latex](−5, 0)[/latex]. |
The x-intercept is [latex](−5, 0)[/latex]. |
| The graph crosses the y-axis at the point [latex](0, −5)[/latex]. |
The y-intercept is [latex](0, −5)[/latex]. |
try it
[ohm_question]146950[/ohm_question]
In the following video, we provide another example of how to find the intercepts of a line from a graph.
https://youtu.be/m5eQ_SjLVuw
Find the Intercepts From an Equation of a Line
Recognizing that the [latex]x\text{-intercept}[/latex] occurs when [latex]y[/latex] is zero and that the [latex]y\text{-intercept}[/latex] occurs when [latex]x[/latex] is zero gives us a method to find the intercepts of a line from its equation.
How to Find the [latex]x[/latex]-intercept and [latex]y[/latex]-intercept Given An Equation of a line
To find the [latex]x\text{-intercept,}[/latex] let [latex]y=0[/latex] and solve for [latex]x[/latex].
To find the [latex]y\text{-intercept}[/latex], let [latex]x=0[/latex] and solve for [latex]y[/latex].
For example, the linear equation [latex]3y+2x=6[/latex] has an x intercept when [latex]y=0[/latex], so [latex]3\left(0\right)+2x=6[/latex].
[latex]\begin{array}{r}2x=6\\x=3\end{array}[/latex]
The x-intercept is [latex](3,0)[/latex].
Likewise the y-intercept occurs when [latex]x=0[/latex].
[latex]\begin{array}{r}3y+2\left(0\right)=6\\3y=6\\y=2\end{array}[/latex]
The y-intercept is [latex](0,2)[/latex].
example
Find the intercepts of [latex]2x+y=6[/latex]
We'll fill in the table below.
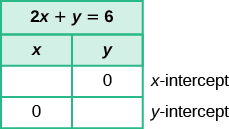
To find the x- intercept, let [latex]y=0[/latex] :
|
[latex]2x+y=6[/latex] |
| Substitute [latex]0[/latex] for y. |
[latex]2x+\color{red}{0}=6[/latex] |
| Add. |
[latex]2x=6[/latex] |
| Divide by [latex]2[/latex]. |
[latex]x=3[/latex] |
| The x-intercept is [latex](3, 0)[/latex]. |
|
To find the y- intercept, let [latex]x=0[/latex] :
|
[latex]2x+y=6[/latex] |
| Substitute [latex]0[/latex] for x. |
[latex]2\cdot\color{red}{0}+y=6[/latex] |
| Multiply. |
[latex]0+y=6[/latex] |
| Add. |
[latex]y=6[/latex] |
| The y-intercept is [latex](0, 6)[/latex]. |
|
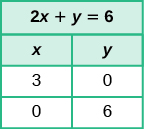
The intercepts are the points [latex]\left(3,0\right)[/latex] and [latex]\left(0,6\right)[/latex] .
try it
[ohm_question]146996[/ohm_question]
example
Find the intercepts of [latex]4x - 3y=12[/latex]
Answer:
Solution
To find the [latex]x\text{-intercept,}[/latex] let [latex]y=0[/latex].
|
[latex]4x - 3y=12[/latex] |
| Substitute [latex]0[/latex] for [latex]y[/latex]. |
[latex]4x - 3\cdot 0=12[/latex] |
| Multiply. |
[latex]4x - 0=12[/latex] |
| Subtract. |
[latex]4x=12[/latex] |
| Divide by [latex]4[/latex]. |
[latex]x=3[/latex] |
The [latex]x\text{-intercept}[/latex] is [latex]\left(3,0\right)[/latex].
To find the [latex]y\text{-intercept}[/latex], let [latex]x=0[/latex].
|
[latex]4x - 3y=12[/latex] |
| Substitute [latex]0[/latex] for [latex]x[/latex]. |
[latex]4\cdot 0 - 3y=12[/latex] |
| Multiply. |
[latex]0 - 3y=12[/latex] |
| Simplify. |
[latex]-3y=12[/latex] |
| Divide by [latex]−3[/latex]. |
[latex]y=-4[/latex] |
The [latex]y\text{-intercept}[/latex] is [latex]\left(0,-4\right)[/latex].
The intercepts are the points [latex]\left(-3,0\right)[/latex] and [latex]\left(0,-4\right)[/latex].
| [latex]4x - 3y=12[/latex] |
| x |
y |
| [latex]3[/latex] |
[latex]0[/latex] |
| [latex]0[/latex] |
[latex]-4[/latex] |
try it
[ohm_question]146997[/ohm_question]
In the following example we show you how to find the intercepts of a line given in a different form than the examples above.
https://youtu.be/vmaMT188ChA
Contribute!
Did you have an idea for improving this content? We’d love your input.
Licenses & Attributions
CC licensed content, Original
- Question ID 146997, 146996, 146950. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: State the X and Y Intercepts Given the Graph of a Line. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
- Ex: Determine the x and y Intercepts of a Linear Equation in Slope Intercept Form. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
 In the graph above, the x-intercept occurs when [latex]x=-2[/latex] and the y-intercept occurs when [latex]y=2[/latex]. We typically express the intercepts by giving the ordered pair, so we say that the x-intercept above is at the point [latex](−2,0)[/latex] and the y-intercept above is at the point [latex](0, 2)[/latex].
Notice that the intercept always occurs where [latex]x=0[/latex], and the x-intercept always occurs where [latex]y=0[/latex].
Let’s look at the graph of the lines shown below.
In the graph above, the x-intercept occurs when [latex]x=-2[/latex] and the y-intercept occurs when [latex]y=2[/latex]. We typically express the intercepts by giving the ordered pair, so we say that the x-intercept above is at the point [latex](−2,0)[/latex] and the y-intercept above is at the point [latex](0, 2)[/latex].
Notice that the intercept always occurs where [latex]x=0[/latex], and the x-intercept always occurs where [latex]y=0[/latex].
Let’s look at the graph of the lines shown below.
 First, notice where each of these lines crosses the x- axis:
First, notice where each of these lines crosses the x- axis:



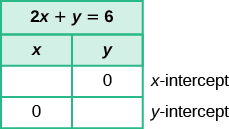 To find the x- intercept, let [latex]y=0[/latex] :
To find the x- intercept, let [latex]y=0[/latex] :
 The intercepts are the points [latex]\left(3,0\right)[/latex] and [latex]\left(0,6\right)[/latex] .
The intercepts are the points [latex]\left(3,0\right)[/latex] and [latex]\left(0,6\right)[/latex] .
