Inconsistent and Dependent Systems in Three Variables
Learning Outcomes
- Express the solution of an inconsistent system of equations containing three variables
- Express the solution of a dependent system of equations containing three variables
Infinitely Many or No Solutions
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as . Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space. The graphic below shows how three planes can intersect to form a line giving the system infinitely many solutions.
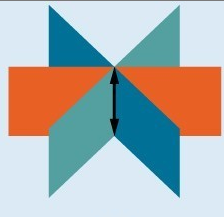 Infinitely many solutions.
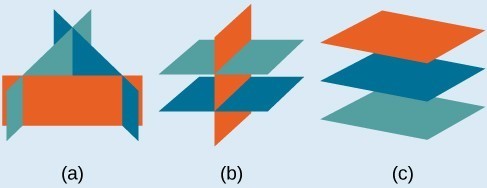
Infinitely many solutions.- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as . Graphically, a system with no solution is represented by three planes with no point in common. Three parallel planes (c), two parallel planes and one intersecting plane (b), three planes that intersect the other two but not at the same location (a).
Example
Solve the following system.
Answer: If you multiply equation by and add and together, you can eliminate y and solve for . First, multiply both sides of equation by .
[latex]\begin{array}\,\,\,\,\,\,2(-y-4z)=2(7)\\-2y-8z=14\end{array}[/latex]
Next, add equations [latex](2)[/latex] and [latex](3)[/latex] together to eliminate y and solve for [latex]z[/latex].
[latex]\begin{array}\,\,\,\,\,\,-2y-8z=14\\\underline{2y+8z=-12}\\0+0=2\\0=2\end{array}[/latex]
Recall that when we were solving systems with two variables, a non-true solution such as [latex]0=2[/latex] implied that there was no solution to the system.
This can happen with a system of three variables as well.
This system has no solution.Example
Find the solution to the given system of three equations in three variables.[latex]\begin{array}{rr}\hfill \text{ }2x+y - 3z=0& \hfill \left(1\right)\\ \hfill 4x+2y - 6z=0& \hfill \left(2\right)\\ \hfill \text{ }x-y+z=0& \hfill \left(3\right)\end{array}[/latex]
Answer: First, we can multiply equation [latex](1)[/latex] by [latex]-2[/latex] and add it to equation [latex](2)[/latex].
[latex]\begin{array}\,-4x−2y+6z=0 \hfill& \text{equation }\left(1\right)\text{multiplied by }−2 \\ \,4x+2y−6z=0\hfill&\left(2\right) \end{array}[/latex]
We do not need to proceed any further. The result we get when adding the two equations is an identity, [latex]0=0[/latex] which tells us that this system has an infinite number of solutions. As shown in the figure below, two of the planes are the same and they intersect the third plane on a line. The solution set is infinite, as all points along the intersection line will satisfy all three equations.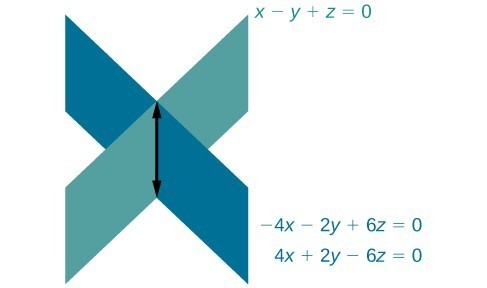
Try It
[ohm_question]183169[/ohm_question]Try It
[ohm_question]183152[/ohm_question]Summary
- A system with three variables can have one, none, or many solutions.
- A system with no solutions will have a non-true result when solving.
- A system with many solutions will have an identity result when solving.
