We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Guías de estudio > ALGEBRA / TRIG I

Radical Expressions and Rational Exponents

Learning Outcomes

  • Convert between radical and exponent notations
Square roots are most often written using a radical sign, like this, [latex] \sqrt{4}[/latex]. But there is another way to represent them. You can use rational exponents instead of a radical. A rational exponent is an exponent that is a fraction. For example, [latex] \sqrt{4}[/latex] can be written as [latex] {{4}^{\tfrac{1}{2}}}[/latex]. Having difficulty imagining a number being raised to a rational power? They may be hard to get used to, but rational exponents can actually help simplify some problems. Writing radicals with rational exponents will come in handy when we discuss techniques for simplifying more complex radical expressions. Radical expressions are expressions that contain radicals. Radical expressions come in many forms, from simple and familiar, such as[latex] \sqrt{16}[/latex], to quite complicated, as in [latex] \sqrt[3]{250{{x}^{4}}y}[/latex]. Radicals and fractional exponents are alternate ways of expressing the same thing.  In the table below we show equivalent ways to express radicals: with a root, with a rational exponent, and as a principal root.

Radical Form

Exponent Form

Principal Root
[latex] \sqrt{16}[/latex] [latex] {{16}^{\tfrac{1}{2}}}[/latex] [latex]4[/latex]
[latex] \sqrt{25}[/latex] [latex] {{25}^{\tfrac{1}{2}}}[/latex] [latex]5[/latex]
[latex] \sqrt{100}[/latex] [latex] {{100}^{\tfrac{1}{2}}}[/latex] [latex]10[/latex]
Use the example below to familiarize yourself with the different ways to write square roots.

Example

Fill in the missing cells in the table.
Exponent Form Root Form Root of a Square Simplified
[latex] {{36}^{\frac{1}{2}}}[/latex]
[latex]\sqrt{81}[/latex]
[latex] \sqrt{{{12}^{2}}}[/latex]

Answer:

Exponent Form Root Form Root of a Square Simplified
[latex] {{36}^{\frac{1}{2}}}[/latex] [latex] \sqrt{36}[/latex] [latex] \sqrt{{{6}^{2}}}[/latex] [latex]6[/latex]
[latex] {{81}^{\frac{1}{2}}}[/latex] [latex] \sqrt{81}[/latex] [latex] \sqrt{{{9}^{2}}}[/latex] [latex]9[/latex]
[latex] {{144}^{\frac{1}{2}}}[/latex] [latex] \sqrt{144}[/latex] [latex]\sqrt{{{12}^{2}}}[/latex] [latex]12[/latex]

In the following video, we show another example of filling in a table to connect the different notation used for roots. https://youtu.be/eGJgmo2CpN4 Let us look at some more examples, but this time with cube roots. Remember, cubing a number raises it to the power of three. Notice that in the examples in the table below, the denominator of the rational exponent is the number [latex]3[/latex].

Radical Form

Exponent Form

Principal Root
[latex] \sqrt[3]{8}[/latex] [latex] {{8}^{\tfrac{1}{3}}}[/latex] [latex]2[/latex]
[latex] \sqrt[3]{125}[/latex] [latex] {{125}^{\tfrac{1}{3}}}[/latex] [latex]5[/latex]
[latex] \sqrt[3]{1000}[/latex] [latex] {{1000}^{\tfrac{1}{3}}}[/latex] [latex]10[/latex]
These examples help us model a relationship between radicals and rational exponents: namely, that the nth root of a number can be written as either [latex] \sqrt[n]{x}[/latex] or [latex] {{x}^{\frac{1}{n}}}[/latex].

Radical Form

Exponent Form
[latex] \sqrt{x}[/latex] [latex] {{x}^{\tfrac{1}{2}}}[/latex]
[latex] \sqrt[3]{x}[/latex] [latex] {{x}^{\tfrac{1}{3}}}[/latex]
[latex] \sqrt[4]{x}[/latex] [latex] {{x}^{\tfrac{1}{4}}}[/latex]
… …
[latex] \sqrt[n]{x}[/latex] [latex] {{x}^{\tfrac{1}{n}}}[/latex]
In the table above, notice how the denominator of the rational exponent determines the index of the root. So, an exponent of [latex] \frac{1}{2}[/latex] translates to the square root, an exponent of [latex] \frac{1}{5}[/latex] translates to the fifth root or [latex] \sqrt[5]{a}[/latex], and [latex] \frac{1}{8}[/latex] translates to the eighth root or [latex] \sqrt[8]{a}[/latex].

Example

Write [latex] \sqrt[4]{81}[/latex] as an expression with a rational exponent.

Answer: The radical form [latex]\sqrt[4]{{a}}[/latex] can be rewritten as the exponent [latex]a^{\frac{1}{4}}[/latex]. Remove the radical and place the exponent next to the base.

[latex]\sqrt[4]{{81}}=81^{\frac{1}{4}}[/latex]

When converting from radical to rational exponent notation, the degree of the root becomes the denominator of the exponent. If you start with a square root, you will have an exponent of [latex]\frac{1}{2}[/latex] on the expression in the radical (the radicand). On the other hand, if you start with an exponent of [latex]\frac{1}{3}[/latex] you will use a cube root. The following statement summarizes this idea.

Writing Fractional Exponents

Any radical in the form [latex]\sqrt[n]{a}[/latex]  can be written using a fractional exponent in the form [latex]a^{\frac{1}{n}}[/latex].

Write an Expression with a Rational Exponent as a Radical

In the following examples, we will show how to convert expressions with rational exponents to expressions with a radical.

Example

Express [latex] {{(2x)}^{^{\frac{1}{3}}}}[/latex] in radical form.

Answer: Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

[latex]\sqrt[3]{2x} [/latex]

The parentheses in [latex] {{\left( 2x \right)}^{\frac{1}{3}}}[/latex] indicate that the exponent refers to everything within the parentheses.

Remember that exponents only refer to the quantity immediately to their left unless a grouping symbol is used. The example below looks very similar to the previous example with one important difference—there are no parentheses! Look what happens.

Example

Express [latex] 2{{x}^{^{\frac{1}{3}}}}[/latex] in radical form.

Answer: Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.

[latex] 2\sqrt[3]{x}[/latex]

The exponent refers only to the part of the expression immediately to the left of the exponent, in this case x, but not the [latex]2[/latex].

Write an Expression with a Radical as a Rational Exponent

Person sitting on the ground with one leg arched behind them and one leg curved in front of them. Flexibility
  We can rewrite radicals using rational exponents.  As we will see when we simplify more complex radical expressions, this can make things easier. Having different ways to express and write algebraic expressions allows us to have flexibility in solving and simplifying them. It is like having a thesaurus when you write. You want to have options for expressing yourself!  

Example

Express [latex] 4\sqrt[3]{xy}[/latex] with rational exponents.

Answer: Rewrite the radical using a rational exponent. The root determines the fraction. In this case, the index of the radical is [latex]3[/latex], so the rational exponent will be [latex] \frac{1}{3}[/latex].

[latex] 4{{(xy)}^{\frac{1}{3}}}[/latex]

Since [latex]4[/latex] is outside the radical, it is not included in the grouping symbol and the exponent does not refer to it.

Rational Exponents Whose Numerator is Not Equal to One

Notice that in the previous two examples, the radicands had exponents.  We simplified these expressions using factorsing, but we can still convert these radical expressions to expressions with rational exponents.  Also, note that all of the numerators for the fractional exponents in the previous examples above were [latex]1[/latex]. You can use fractional exponents that have numerators other than [latex]1[/latex] to express roots, as shown below.

Radical

Exponent
[latex] \sqrt{9}[/latex] [latex]9^{\frac{1}{2}}[/latex]
[latex] \sqrt[3]{{{9}^{2}}}[/latex] [latex]9^{\frac{2}{3}}[/latex]
[latex]\sqrt[4]{9^{3}}[/latex] [latex]9^{\frac{3}{4}}[/latex]
[latex]\sqrt[5]{9^{2}}[/latex] [latex]9^{\frac{2}{5}}[/latex]
… …
[latex]\sqrt[n]{9^{x}}[/latex] [latex]9^{\frac{x}{n}}[/latex]
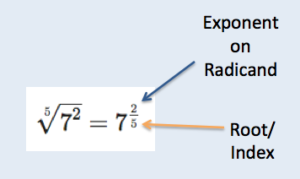Screen Shot 2016-07-29 at 3.56.45 PM To rewrite a radical using a fractional exponent, the power to which the radicand is raised becomes the numerator and the root/index becomes the denominator.

Writing Rational Exponents

Any radical in the form [latex]\sqrt[n]{a^{x}}[/latex]  can be written using a fractional exponent in the form [latex]a^{\frac{x}{n}}[/latex].
The relationship between [latex] \sqrt[n]{{{a}^{x}}}[/latex]and [latex] {{a}^{\frac{x}{n}}}[/latex] works for rational exponents that have a numerator of [latex]1[/latex] as well. For example, the radical [latex] \sqrt[3]{8}[/latex] can also be written as [latex] \sqrt[3]{{{8}^{1}}}[/latex], since any number remains the same value if it is raised to the first power. You can now see where the numerator of [latex]1[/latex] comes from in the equivalent form of [latex] {{8}^{\frac{1}{3}}}[/latex]. In the next example, we practice writing radicals with rational exponents where the numerator is not equal to one.

Example

Rewrite the radicals using a rational exponent, then simplify your result.
  1. [latex]\sqrt[3]{{{a}^{6}}}[/latex]
  2. [latex]\sqrt[12]{16^3}[/latex]

Answer: 1.[latex]\sqrt[n]{a^{x}}[/latex] can be rewritten as [latex]a^{\frac{x}{n}}[/latex], so in this case [latex]n=3,\text{ and }x=6[/latex], therefore [latex-display]\sqrt[3]{{{a}^{6}}}={{a}^{\frac{6}{3}}}[/latex-display] Simplify the exponent. [latex-display]{{a}^{\frac{6}{3}}}={{a}^{2}}[/latex-display] 2. [latex]\sqrt[n]{a^{x}}[/latex] can be rewritten as [latex]a^{\frac{x}{n}}[/latex], so in this case [latex]n=12,\text{ and }x=3[/latex], therefore

[latex]\sqrt[12]{16^3}={16}^{\frac{3}{12}}={16}^{\frac{1}{4}}[/latex]

Simplify the expression using rules for exponents. [latex-display]{16}^{\frac{1}{4}}=2[/latex-display]

Try It

[ohm_question]3537[/ohm_question]
In our last example we will rewrite expressions with rational exponents as radicals. This practice will help us when we simplify more complicated radical expressions and as we learn how to solve radical equations. Typically it is easier to simplify when we use rational exponents, but this exercise is intended to help you understand how the numerator and denominator of the exponent are the exponent of a radicand and index of a radical.

Example

Rewrite the expressions using a radical.
  1. [latex]{x}^{\frac{2}{3}}[/latex]
  2. [latex]{5}^{\frac{4}{7}}[/latex]

Answer:

  1. [latex]{x}^{\frac{2}{3}}[/latex], the numerator is [latex]2[/latex] and the denominator is [latex]3[/latex], therefore we will have the third root of x squared, [latex]\sqrt[3]{x^2}[/latex]
  2. [latex]{5}^{\frac{4}{7}}[/latex], the numerator is [latex]4[/latex] and the denominator is [latex]7[/latex], so we will have the seventh root of [latex]5[/latex] raised to the fourth power. [latex]\sqrt[7]{5^4}[/latex]

 
In the following video, we show more examples of writing radical expressions with rational exponents and expressions with rational exponents as radical expressions. https://youtu.be/5cWkVrANBWA We will use this notation later, so come back for practice if you forget how to write a radical with a rational exponent.

Summary

Any radical in the form [latex]\sqrt[n]{a^{x}}[/latex] can be written using a fractional exponent in the form [latex]a^{\frac{x}{n}}[/latex]. Rewriting radicals using fractional exponents can be useful when simplifying some radical expressions. When working with fractional exponents, remember that fractional exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Licenses & Attributions

CC licensed content, Original

  • Write Expressions Using Radicals and Rational Exponents. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Precalculus. Provided by: OpenStax Authored by: Abramson, Jay. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: Public Domain: No Known Copyright. License terms: Dwonload fro free at : http://cnx.org/contents/[email protected]:1/Preface.