We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > ALGEBRA / TRIG I

Square Roots and Completing the Square

Learning Outcomes

  • Use the square root property to solve a quadratic equation
  • Complete the square to solve a quadratic equation with irrational roots
Quadratic equations can be solved using many methods. You may already be familiar with factoring to solve some quadratic equations. However, not all quadratic equations can be factored. In this section, you will use square roots to learn another way to solve quadratic equations—and this method will work with all quadratic equations.

Solve a Quadratic Equation by the Square Root Property

One way to solve the quadratic equation [latex]x^{2}=9[/latex] is to subtract [latex]9[/latex] from both sides to get one side equal to 0: [latex]x^{2}-9=0[/latex]. The expression on the left can be factored; it is a difference of squares: [latex]\left(x+3\right)\left(x–3\right)=0[/latex]. Using the zero factor property, you know this means [latex]x+3=0[/latex] or [latex]x–3=0[/latex], so [latex]x=−3[/latex] or [latex]3[/latex]. Another property that would let you solve this equation more easily is called the square root property.

The Square Root Property

If [latex]x^{2}=a[/latex], then [latex] x=\sqrt{a}[/latex] or [latex] -\sqrt{a}[/latex].   The solutions of [latex]x^2=a[/latex] are called the square roots of a.
  • When a is positive, [latex]a > 0[/latex], [latex]x^2=a[/latex] has two solutions, [latex]+\sqrt{a},-\sqrt{a}[/latex]. [latex]+\sqrt{a}[/latex] is the nonnegative square root of a, and [latex]-\sqrt{a}[/latex] is the negative square root of a.
  • When a is negative, [latex]a < 0[/latex], [latex]x^2=a[/latex] has no solutions.
  • When a is zero, [latex]a = 0[/latex], [latex]x^2=a[/latex] has one solution: [latex]a = 0[/latex]
A shortcut way to write “[latex] \sqrt{a}[/latex]” or “[latex] -\sqrt{a}[/latex]” is [latex] \pm \sqrt{a}[/latex]. The symbol [latex]\pm[/latex] is often read “positive or negative.” If it is used as an operation (addition or subtraction), it is read “plus or minus.”

Example

Solve using the Square Root Property. [latex]x^{2}=9[/latex]

Answer: Since one side is simply [latex]x^{2}[/latex], you can take the square root of both sides to get x on one side. Do not forget to use both positive and negative square roots!

[latex]\begin{array}{c}x^{2}=9 \\ x=\pm\sqrt{9} \end{array}[/latex]

[latex]x=\pm3[/latex] (that is, [latex]x=3[/latex] or [latex]-3[/latex])

Notice that there is a difference here in solving [latex]x^{2}=9[/latex] and finding [latex] \sqrt{9}[/latex]. For [latex]x^{2}=9[/latex], you are looking for all numbers whose square is [latex]9[/latex]. For [latex] \sqrt{9}[/latex], you only want the principal (nonnegative) square root. The negative of the principal square root is [latex] -\sqrt{9}[/latex]; both would be [latex] \pm \sqrt{9}[/latex]. Unless there is a symbol in front of the radical sign, only the nonnegative value is wanted! In the example above, you can take the square root of both sides easily because there is only one term on each side. In some equations, you may need to do some work to get the equation in this form. You will find that this involves isolating [latex]x^{2}[/latex]. In our first video, we will show more examples of using the square root property to solve a quadratic equation. https://youtu.be/Fj-BP7uaWrI

Example

Solve. [latex]10x^{2}+5=85[/latex]

Answer: If you try taking the square root of both sides of the original equation, you will have [latex] \sqrt{10{{x}^{2}}+5}[/latex] on the left, and you cannot simplify that. Subtract [latex]5[/latex] from both sides to get the [latex]x^{2}[/latex] term by itself.

[latex]10x^{2}=80[/latex]

You could now take the square root of both sides, but you would have [latex] \sqrt{10}[/latex] as a coefficient, and you would need to divide by that coefficient. Dividing by [latex]10[/latex] before you take the square root will be a little easier.

[latex]x^{2}=8[/latex]

Now you have only [latex]x^{2}[/latex] on the left, so you can use the Square Root Property easily. Be sure to simplify the radical if possible.

[latex] \begin{array}{ll}{{x}^{2}} & =8\\ x & =\pm \sqrt{8}\\ & =\pm \sqrt{(4)(2)}\\ & =\pm \sqrt{4}\sqrt{2}\\ & =\pm 2\sqrt{2}\end{array}[/latex]

The answer is [latex] x=\pm 2\sqrt{2}[/latex].

Try It

[ohm_question]197330[/ohm_question]
Sometimes more than just the [latex]x[/latex] is being squared:

Example

Solve. [latex]\left(x–2\right)^{2}–50=0[/latex]

Answer: Again, taking the square root of both sides at this stage will leave something you cannot work with on the left. Start by adding 50 to both sides.

[latex]\left(x-2\right)^{2}=50[/latex]

Because [latex]\left(x–2\right)^{2}[/latex] is a squared quantity, you can take the square root of both sides.

[latex]\begin{array}{r}\left(x-2\right)^{2}=50 \\ x-2=\pm\sqrt{50}\end{array}[/latex]

To isolate [latex]x[/latex] on the left, you need to add [latex]2[/latex] to both sides. Be sure to simplify the radical if possible.

[latex] \begin{array}{ll}x & =2\pm \sqrt{50} \\ & =2\pm \sqrt{(25)(2)} \\ & =2\pm \sqrt{25}\sqrt{2} \\ & =2\pm 5\sqrt{2}\end{array}[/latex]

The answer is [latex] x=2\pm 5\sqrt{2}[/latex].

In the next video, you will see more examples of using square roots to solve quadratic equations. https://youtu.be/4H5qZ_-8YM4

Solve a Quadratic Equation by Completing the Square

Not all quadratic equations can be factored or solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square. Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. Some of the above examples have squared binomials: [latex]\left(1+r\right)^{2}[/latex] and [latex]\left(x–2\right)^{2}[/latex] are squared binomials. If you expand these, you get a perfect square trinomial. Perfect square trinomials have the form [latex]x^{2}+2xs+s^{2}[/latex] and can be factored as [latex]\left(x+s\right)^{2}[/latex], or they have the form [latex]x^{2}–2xs+s^{2}[/latex] and can be factored as [latex]\left(x–s\right)^{2}[/latex]. Let’s factor a perfect square trinomial into a squared binomial.

Example

Factor [latex]9x^{2}–24x+16[/latex].

Answer: First notice that the [latex]x^{2}[/latex] term and the constant term are both perfect squares. [latex-display]\begin{array}{l}9x^{2}=\left(3x\right)^{2} \\ 16=4^{2}\end{array}[/latex-display] Then notice that the middle term (ignoring the sign) is twice the product of the square roots of these squared terms. [latex-display]24x=2\left(3x\right)\left(4\right)[/latex-display] A trinomial in the form [latex]r^{2}-2rs+s^{2}[/latex] can be factored as [latex](r–s)^{2}[/latex]. In this case, the middle term is subtracted, so subtract r and s and square it to get [latex](r–s)^{2}[/latex]. [latex-display]\begin{array}{c}\,\,\,r=3x\\s=4\\9x^{2}-24x+16=\left(3x-4\right)^{2}\end{array}[/latex-display]

If this were an equation, we could solve using either the square root property or the zero product property. You can use the same procedure in this next example to help you solve equations where you identify perfect square trinomials, even if the equation is not set equal to [latex]0[/latex].

Example

Solve. [latex]4x^{2}+20x+25=8[/latex]

Answer: Since there’s an x term, you can’t use the Square Root Property immediately (or even after adding or dividing by a constant). Notice, however, that the [latex]x^{2}[/latex] and constant terms on the left are both perfect squares: [latex]\left(2x\right)^{2}[/latex] and [latex]5^{2}[/latex]. Check the middle term: is it [latex]2\left(2x\right)\left(5\right)[/latex]? Yes!

[latex]4x^{2}+20x+25=8[/latex]

A trinomial in the form [latex]r^{2}+2rs+s^{2}[/latex] can be factored as [latex]\left(r+s\right)^{2}[/latex], so rewrite the left side as a squared binomial.

[latex](2x+5)^{2}=8[/latex]

Now you can use the Square Root Property. Some additional steps are needed to isolate x.

[latex] \begin{array}{r}2x+5=\pm \sqrt{8}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\2x=-5\pm \sqrt{8}\,\,\,\,\,\\\\x=-\frac{5}{2}\pm \frac{1}{2}\sqrt{8}\end{array}[/latex]

Simplify the radical when possible.

[latex] \begin{array}{l}x=-\frac{5}{2}\pm \frac{1}{2}\sqrt{4}\sqrt{2}\\\\x=-\frac{5}{2}\pm \frac{1}{2}(2)\sqrt{2}\\\\x=-\frac{5}{2}\pm \sqrt{2}\end{array}[/latex]

Answer

[latex-display] x=-\frac{5}{2}\pm \sqrt{2}[/latex-display]

One way to solve quadratic equations is by completing the square. When you don’t have a perfect square trinomial, you can create one by adding a constant term that is a perfect square to both sides of the equation. Let’s see how to find that constant term. “Completing the square” does exactly what it says—it takes something that is not a square and makes it one. This idea can be illustrated using an area model of the binomial [latex]x^{2}+bx[/latex]. X times X is x squared. X times b is bx. x(x+b)=x^{2}+bx In this example, the area of the overall rectangle is given by [latex]x\left(x+b\right)[/latex]. Now let's make this rectangle into a square. First, divide the red rectangle with area bx into two equal rectangles each with area [latex] \frac{b}{2}x[/latex]. Then rotate and reposition one of them. You haven't changed the size of the red area—it still adds up to [latex]bx[/latex].
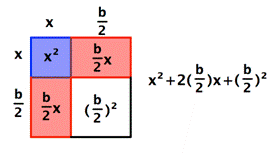X times X is X squared. X times b/2 is equal to b/2 x. X times b/2 is equal to b/2 x. X times X is X squared. X times b/2 is equal to b/2 x. X times b/2 is equal to b/2 x. B\2 times b\2 is b\2 squared. X squared plus 2 times b\2 x + b\2 squared
The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex]. Here comes the cool part—do you see that when the white square is added to the blue and red regions, the whole shape is also now a square? In other words, you've "completed the square!" By adding the quantity [latex]\left(\frac{b}{2}\right)^{2}[/latex] to the original binomial, you've made a square, a square with sides of [latex]x+\frac{b}{2}[/latex]. X times X is X squared. X times b/2 is equal to b/2 x. X times b/2 is equal to b/2 x. B\2 times b\2 is b\2 squared. The lengths of the overall square is now x + b\2. X squared +bx+ b\2 squared equals x squared + 2 times b\2 x + b\2 squared = the square of x + b\2. Notice that the area of this square can be written as a squared binomial: [latex]\left(x+\frac{b}{2}\right)^{2}[/latex].

Finding a Value that will Complete the Square in an Expression

To complete the square for an expression of the form [latex]x^{2}+bx[/latex]:
  • Identify the value of b;
  • Calculate and add [latex]\left(\frac{b}{2}\right)^{2}[/latex].
The expression becomes [latex]x^{2}+bx+\left(\frac{b}{2}\right)^{2}=\left(x+\frac{b}{2}\right)^{2}[/latex].

Example

Find the number to add to [latex]x^{2}+8x[/latex] to make it a perfect square trinomial.

Answer: First identify b if this has the form [latex]x^{2}+bx[/latex].

[latex]\begin{array}{c}x^{2}+8x\\b=8\end{array}[/latex]

To complete the square, add [latex]\left(\frac{b}{2}\right)^{2}[/latex].

[latex]b=8[/latex], so [latex]\left(\frac{b}{2}\right)^{2}=\left(\frac{8}{2}\right)^{2}[/latex]

Simplify.

[latex]\begin{array}{c}x^{2}+8x+\left(4\right)^{2}\\x^{2}+8x+16\end{array}[/latex]

Check that the result is a perfect square trinomial. [latex]\left(x+4\right)^{2}=x^{2}+4x+4x+16=x^{2}+8x+16[/latex], so it is.

Answer

Adding [latex]+16[/latex] will make [latex]x^{2}+8x[/latex] a perfect square trinomial.

Notice that [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] is always positive, since it is the square of a number. When you complete the square, you are always adding a positive value. In the following video, we show more examples of how to find a constant term that will make a trinomial a perfect square. https://youtu.be/vt-pM1LEP1M You can use completing the square to help you solve a quadratic equation that cannot be solved by factoring (and it will still work even when you can factor!). Let’s start by seeing what happens when you complete the square in an equation. In the example below, notice that completing the square will result in adding a number to both sides of the equation—you have to do this in order to keep both sides equal!

Example

Rewrite [latex]x^{2}+6x=8[/latex] so that the left side is a perfect square trinomial.

Answer: This equation has a constant of 8. Ignore it for now and focus on the [latex]x^{2}[/latex] and x terms on the left side of the equation. The left side has the form [latex]x^{2}+bx[/latex], so you can identify b.

[latex]\begin{array}{r}x^{2}+6x=8\\b=6\end{array}[/latex]

To complete the square, add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] to the left side. [latex-display]b=6[/latex], so [latex] {{\left( \frac{b}{2} \right)}^{2}}={{\left( \frac{6}{2} \right)}^{2}}={{3}^{2}}=9.[/latex-display] This is an equation, though, so you must add the same number to the right side as well.

[latex]x^{2}+6x+9=8+9[/latex]

Simplify. Check that the left side is a perfect square trinomial. [latex]\begin{array}{r}\left(x+3\right)^{2}=x^{2}+3x+3x+9=x^{2}+6x+9\end{array}{r}[/latex], so it is.

[latex]\begin{array}{r}x^{2}+6x+9=17\\x^{2}+6x+9=17\\(x+3)^{2}=17\end{array}[/latex]

Answer

[latex-display]x^{2}+6x+9=17[/latex-display]

Can you see that completing the square in an equation is very similar to completing the square in an expression? The main difference is that you have to add the new number ([latex]+9[/latex] in this case) to both sides of the equation to maintain equality. Now let’s look at an example where you are using completing the square to actually solve an equation, finding a value for the variable.

Example

Solve. [latex]x^{2}–12x–4=0[/latex]

Answer: Since you cannot factor the trinomial on the left side, you will use completing the square to solve the equation. Rewrite the equation with the left side in the form [latex]x^{2}+bx[/latex], to prepare to complete the square. Identify b.

[latex]\begin{array}{r}x^{2}-12x=4\,\,\,\,\,\,\,\,\\b=-12\end{array}[/latex]

Figure out what value to add to complete the square. Add [latex] {{\left( \frac{b}{2}\right)}^{2}}[/latex] to complete the square, so [latex] {{\left( \frac{b}{2} \right)}^{2}}={{\left( \frac{-12}{2} \right)}^{2}}={{\left( -6 \right)}^{2}}=36[/latex]. Add the value to both sides of the equation and simplify.

[latex]\begin{array}{l}x^{2}-12x+36=4+36\\x^{2}-12x+36=40\end{array}[/latex]

Rewrite the left side as a squared binomial.

[latex]\left(x-6\right)^{2}=40[/latex]

Use the Square Root Property. Remember to include both the positive and negative square root, or you’ll miss one of the solutions.

[latex] x-6=\pm\sqrt{40}[/latex]

Solve for x by adding 6 to both sides. Simplify as needed.

[latex] \begin{array}{l}x=6\pm \sqrt{40}\\\,\,\,\,=6\pm \sqrt{4}\sqrt{10}\\\,\,\,\,=6\pm 2\sqrt{10}\end{array}[/latex]

Answer

[latex-display] x=6\pm 2\sqrt{10}[/latex-display]

Notice that, to complete the square, the leading coefficient, a, must equal 1. If it does not, then divide the entire equation by a. Then, we can use the following procedures to solve a quadratic equation by completing the square.

Steps for Completing The Square

  1. Given a quadratic equation with [latex]a=1[/latex], first add or subtract the constant term c to the right side of the equal sign.
    [latex]{x}^{2}+bx=-c[/latex]
  2. Multiply the b term by [latex]\frac{1}{2}[/latex] and square it.
    [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex]
  3. Add [latex]{\left(\frac{1}{2}b\right)}^{2}[/latex] to both sides of the equal sign and simplify the right side
  4. The left side of the equation can now be factored as a perfect square.  [latex]x^{2}+bx+\left(\frac{b}{2}\right)^{2}=\left(x+\frac{b}{2}\right)^{2}[/latex]
  5. Use the square root property to solve.

Try It

[ohm_question]147603[/ohm_question]
 

Example

Solve by completing the square: [latex]{x}^{2}-3x - 5=0[/latex].

Answer: First, move the constant term to the right side of the equal sign.

[latex]{x}^{2}-3x=5[/latex]
Identify [latex]b[/latex]:   [latex]b=-3[/latex] Then, take [latex]\frac{1}{2}[/latex] of the b term and square it.
[latex]\begin{array}{l}\frac{1}{2}\left(-3\right)=-\frac{3}{2}\hfill \\ {\left(-\frac{3}{2}\right)}^{2}=\frac{9}{4}\hfill \end{array}[/latex]
Add the result to both sides of the equal sign.
[latex]\begin{array}{l}\text{ }{x}^{2}-3x+{\left(-\frac{3}{2}\right)}^{2}=5+{\left(-\frac{3}{2}\right)}^{2}\hfill \\ {x}^{2}-3x+\frac{9}{4}=5+\frac{9}{4}\hfill \end{array}[/latex]
Factor the left side as a perfect square and simplify the right side.
[latex]{\left(x-\frac{3}{2}\right)}^{2}=\frac{29}{4}[/latex]
Use the square root property and solve.
[latex]\begin{array}{rl}\sqrt{{\left(x-\frac{3}{2}\right)}^{2}}\hfill & = \pm \sqrt{\frac{29}{4}}\hfill \\ x-\frac{3}{2} & =\pm \frac{\sqrt{29}}{2}\hfill \\ x & =\frac{3}{2}\pm \frac{\sqrt{29}}{2}\hfill \end{array}[/latex]
The solutions are [latex]x=\frac{3+\sqrt{29}}{2}[/latex], [latex]x=\frac{3-\sqrt{29}}{2}[/latex].

In the next video, you will see more examples of how to use completing the square to solve a quadratic equation. https://youtu.be/PsbYUySRjFo You may have noticed that because you have to use both square roots, all the examples have two solutions. Here is another example that is slightly different.

Example

Solve by completing the square. [latex]x^{2}+16x+17=-47[/latex].

Answer: Rewrite the equation so the left side has the form [latex]x^{2}+bx[/latex]. Identify b.

[latex]\begin{array}{c}x^{2}+16x=-64\\b=16\end{array}[/latex]

Add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex], which is [latex] {{\left( \frac{16}{2} \right)}^{2}}={{8}^{2}}=64[/latex], to both sides.

[latex]\begin{array}{l}x^{2}+16x+64=-64+64\\x^{2}+16x+64=0\end{array}[/latex]

Write the left side as a squared binomial.

[latex]\left(x+8\right)^{2}=0[/latex]

Take the square roots of both sides. Normally both positive and negative square roots are needed, but 0 is neither positive nor negative. [latex]0[/latex] has only one root.

[latex]x+8=0[/latex]

[latex]x=-8[/latex]

Take a closer look at this problem and you may see something familiar. Instead of completing the square, try adding [latex]47[/latex] to both sides in the equation. The equation [latex]x^{2}+16x+17=−47[/latex] becomes [latex]x^{2}+16x+64=0[/latex]. Can you factor this equation using grouping? (Think of two numbers whose product is 64 and whose sum is [latex]16[/latex]). It can be factored as [latex](x+8)(x+8)=0[/latex], of course! Knowing how to complete the square is very helpful, but it is not always the only way to solve an equation. In our last video, we show an example of how to use completing the square to solve a quadratic equation whose solutions are irrational. https://youtu.be/IjCjbtrPWHM

Summary

Completing the square is used to change a binomial of the form [latex]x^{2}+bx[/latex] into a perfect square trinomial [latex] {{x}^{2}}+bx+{{\left( \frac{b}{2} \right)}^{2}}[/latex] which can be factored to [latex] {{\left( x+\frac{b}{2} \right)}^{2}}[/latex]. When solving quadratic equations by completing the square, be careful to add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] to both sides of the equation to maintain equality. The Square Root Property can then be used to solve for [latex]x[/latex]. With the Square Root Property, be careful to include both the principal square root and its opposite. Be sure to simplify as needed.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Licenses & Attributions

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at: http://cnx.org/contents/[email protected]:1/Preface.
  • Ex 1: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 2: Solving Quadratic Equations Using Square Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 1: Completing the Square - Real Rational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 2: Completing the Square - Real Irrational Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.