Using the Properties of Rectangles to Solve Problems
Learning Outcomes
- Use properties of rectangles
 The perimeter, [latex]P[/latex], of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk [latex]L+W+L+W[/latex] units, or two lengths and two widths. The perimeter then is
The perimeter, [latex]P[/latex], of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk [latex]L+W+L+W[/latex] units, or two lengths and two widths. The perimeter then is
[latex]\begin{array}{c}P=L+W+L+W\hfill \\ \hfill \text{or}\hfill \\ P=2L+2W\hfill \end{array}[/latex]
What about the area of a rectangle? Remember the rectangular rug from the beginning of this section. It was [latex]2[/latex] feet long by [latex]3[/latex] feet wide, and its area was [latex]6[/latex] square feet. See the image below. Since [latex]A=2\cdot 3[/latex], we see that the area, [latex]A[/latex], is the length, [latex]L[/latex], times the width, [latex]W[/latex], so the area of a rectangle is [latex]A=L\cdot W[/latex]. The area of this rectangular rug is [latex]6[/latex] square feet, its length times its width.
Properties of Rectangles
- Rectangles have four sides and four right [latex]\left(\text{90}^ \circ\right)[/latex] angles.
- The lengths of opposite sides are equal.
- The perimeter, [latex]P[/latex], of a rectangle is the sum of twice the length and twice the width. See the first image. [latex]P=2L+2W[/latex]
- The area, [latex]A[/latex], of a rectangle is the length times the width. [latex]A=L\cdot W[/latex]
Use a Problem Solving Strategy for Geometry Applications
- Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
example
The length of a rectangle is [latex]32[/latex] meters and the width is [latex]20[/latex] meters. 1. Find the perimeter 2. Find the area Solution| 1. | |
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | the perimeter of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let [latex]P[/latex] = the perimeter |
| Step 4. Translate. Write the appropriate formula. Substitute. |  |
| Step 5. Solve the equation. | [latex]P=64m+40m[/latex] [latex]P=104m[/latex] |
| Step 6. Check: [latex-display]p\stackrel{?}{=}104m[/latex-display] [latex-display]20m+32m+20m+32m\stackrel{?}{=}104m[/latex-display] [latex]104m=104m\checkmark[/latex] | |
| Step 7. Answer the question. | The perimeter of the rectangle is [latex]104[/latex] meters. |
| 2. | |
| Step 1. Read the problem. Draw the figure and label it with the given information. |  |
| Step 2. Identify what you are looking for. | the area of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4. Translate. Write the appropriate formula. Substitute. |  |
| Step 5. Solve the equation. | [latex]A=640m^2[/latex] |
| Step 6. Check: [latex-display]A\stackrel{?}{=}640m^2[/latex-display] [latex-display]32m\cdot 20m\stackrel{?}{=}640m^2[/latex-display] [latex]640m^2=640m^2\checkmark[/latex] | |
| Step 7. Answer the question. | The area of the rectangle is [latex]640[/latex] square meters. |
try it
[ohm_question]146510[/ohm_question]example
Find the length of a rectangle with perimeter [latex]50[/latex] inches and width [latex]10[/latex] inches.Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 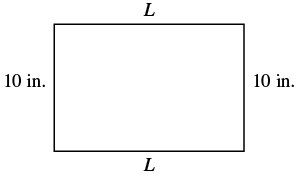 |
| Step 2. Identify what you are looking for. | the length of the rectangle |
| Step 3. Name. Choose a variable to represent it. | Let [latex]L[/latex] = the length |
| Step 4. Translate. Write the appropriate formula. Substitute. | 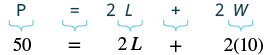 |
| Step 5. Solve the equation. | [latex]50\color{red}{- 20}=2L+20\color{red}{- 20}[/latex] [latex-display]30=2L[/latex-display] [latex-display]{\Large\frac{30}{\color{red}{2}}}={\Large\frac{2L}{\color{red}{2}}}[/latex-display] [latex]15=L[/latex] |
| Step 6. Check: [latex-display]p=50[/latex-display] [latex-display]15+10+15+10\stackrel{?}{=}50[/latex-display] [latex]50=50\checkmark[/latex] | |
| Step 7. Answer the question. | The length is [latex]15[/latex] inches. |
try it
[ohm_question]146518[/ohm_question]example
The width of a rectangle is two inches less than the length. The perimeter is [latex]52[/latex] inches. Find the length and width.Answer: Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width of the rectangle |
| Step 3. Name. Choose a variable to represent it. Now we can draw a figure using these expressions for the length and width. | Since the width is defined in terms of the length, we let L = length. The width is two feet less that the length, so we let L − 2 = width
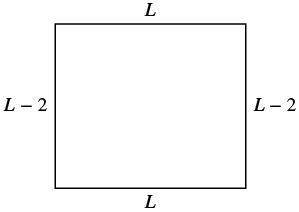 |
| Step 4.Translate. Write the appropriate formula. The formula for the perimeter of a rectangle relates all the information. Substitute in the given information. | 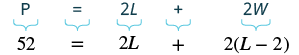 |
| Step 5. Solve the equation. | [latex]52=2L+2L - 4[/latex] |
| Combine like terms. | [latex]52=4L - 4[/latex] |
| Add [latex]4[/latex] to each side. | [latex]56=4L[/latex] |
| Divide by [latex]4[/latex]. | [latex]{\Large\frac{56}{4}}={\Large\frac{4L}{4}}[/latex] |
| [latex]14=L[/latex] | |
| The length is [latex]14[/latex] inches. | |
| Now we need to find the width. | [latex]L-2[/latex] [latex-display]\color{red}{14}-2[/latex-display] [latex]12[/latex] |
| The width is [latex]L−2[/latex]. | The width is [latex]12[/latex] inches. |
| Step 6. Check: Since [latex]14+12+14+12=52[/latex] , this works! | |
| Step 7. Answer the question. | The length is [latex]14[/latex] feet and the width is [latex]12[/latex] feet. |
try it
[ohm_question]146504[/ohm_question]example
The length of a rectangle is four centimeters more than twice the width. The perimeter is [latex]32[/latex] centimeters. Find the length and width.Answer: Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width |
| Step 3. Name. Choose a variable to represent it. | let W = width
The length is four more than twice the width.
[latex]2w+4[/latex] = length
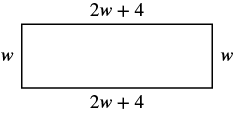 |
| Step 4.Translate. Write the appropriate formula and substitute in the given information. | 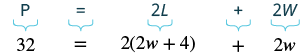 |
| Step 5. Solve the equation. | [latex]32=4w+8+2w[/latex] [latex-display]32=6w+8[/latex-display] [latex-display]24=6w[/latex-display] [latex]4=w[/latex] (width) [latex]2w+4=[/latex] length [latex-display]2(\color{red}{4})+4[/latex-display] [latex-display]8+4=12[/latex-display] The length is [latex]12[/latex]cm. |
| Step 6. Check: [latex-display]P=2L+2W[/latex-display] [latex-display]P\stackrel{?}{=}2\cdot 12+2\cdot 4[/latex-display] [latex]32=32\quad\checkmark[/latex] | |
| Step 7. Answer the question. | The length is [latex]12[/latex] cm and the width is [latex]4[/latex] cm. |
try it
[ohm_question]146521[/ohm_question] [ohm_question]146522[/ohm_question]example
The area of a rectangular room is [latex]168[/latex] square feet. The length is [latex]14[/latex] feet. What is the width?Answer: Solution
| Step 1. Read the problem. | 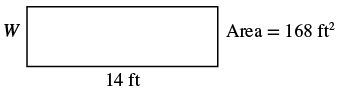 |
| Step 2. Identify what you are looking for. | the width of a rectangular room |
| Step 3. Name. Choose a variable to represent it. | Let W = width |
| Step 4.Translate. Write the appropriate formula and substitute in the given information. | [latex]A=LW[/latex] [latex]168=14W[/latex] |
| Step 5. Solve the equation. | [latex]\Large\frac{168}{14}\normalsize= \Large\frac{14W}{14}[/latex] [latex]12=W[/latex] |
| Step 6. Check: [latex-display]A=LW[/latex-display] [latex-display]168\stackrel{?}{=}14\cdot 12[/latex-display] [latex]168=168\checkmark[/latex] | |
| Step 7. Answer the question. | The width of the room is [latex]12[/latex] feet. |
try it
[ohm_question]146523[/ohm_question]example
The perimeter of a rectangular swimming pool is [latex]150[/latex] feet. The length is [latex]15[/latex] feet more than the width. Find the length and width.Answer: Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 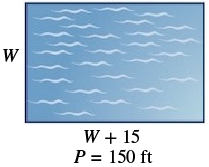 |
| Step 2. Identify what you are looking for. | the length and width of the pool |
| Step 3. Name. Choose a variable to represent it. The length is [latex]15[/latex] feet more than the width. | Let [latex]W=\text{width}[/latex] [latex]W+15=\text{length}[/latex] |
| Step 4.Translate. Write the appropriate formula and substitute. | 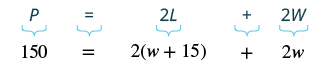 |
| Step 5. Solve the equation. | [latex]150=2w+30+2w[/latex] [latex-display]150=4w+30[/latex-display] [latex-display]120=4w[/latex-display] [latex]30=w[/latex] the width of the pool. [latex]w+15[/latex] the length of the pool. [latex-display]\color{red}{30}+15[/latex-display] [latex]45[/latex] |
| Step 6. Check: [latex-display]P=2L+2W[/latex-display] [latex-display]150\stackrel{?}{=}2(45)+2(30)[/latex-display] [latex]150=150\checkmark[/latex] | |
| Step 7. Answer the question. | The length of the pool is [latex]45[/latex] feet and the width is [latex]30[/latex] feet. |
try it
[ohm_question]146524[/ohm_question]Contribute!
Did you have an idea for improving this content? We’d love your input.
Licenses & Attributions
CC licensed content, Original
- Question ID 146524, 146522, 146518, 146504. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: Find the Area of a Rectangle Given the Perimeter. Authored by: James Sousa (amthispower4u.com). License: CC BY: Attribution.
- Find the Width of a Rectangle Given the Perimeter / Literal Equation. Authored by: James Sousa (mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
