One-Sided Limits
Learning Objectives
- Define one-sided limits and provide examples.
- Explain the relationship between one-sided and two-sided limits.
- Define a vertical asymptote.
One-Sided Limits
Sometimes indicating that the limit of a function fails to exist at a point does not provide us with enough information about the behavior of the function at that particular point. To see this, we now revisit the function [latex]g(x)=|x-2|/(x-2)[/latex] introduced at the beginning of the section (see (Figure)(b)). As we pick values of [latex]x[/latex] close to 2, [latex]g(x)[/latex] does not approach a single value, so the limit as [latex]x[/latex] approaches 2 does not exist—that is, [latex]\underset{x\to 2}{\lim}g(x)[/latex] DNE. However, this statement alone does not give us a complete picture of the behavior of the function around the [latex]x[/latex]-value 2. To provide a more accurate description, we introduce the idea of a one-sided limit. For all values to the left of 2 (or the negative side of 2), [latex]g(x)=-1[/latex]. Thus, as [latex]x[/latex] approaches 2 from the left, [latex]g(x)[/latex] approaches −1. Mathematically, we say that the limit as [latex]x[/latex] approaches 2 from the left is −1. Symbolically, we express this idea as
Similarly, as [latex]x[/latex] approaches 2 from the right (or from the positive side), [latex]g(x)[/latex] approaches 1. Symbolically, we express this idea as
We can now present an informal definition of one-sided limits.
Definition
We define two types of one-sided limits.
Limit from the left: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form z, and let [latex]L[/latex] be a real number. If the values of the function [latex]f(x)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]x<a[/latex]) approach the number [latex]a[/latex], then we say that [latex]L[/latex] is the limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches a from the left. Symbolically, we express this idea as
Limit from the right: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](a,c)[/latex], and let [latex]L[/latex] be a real number. If the values of the function [latex]f(x)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]x>a[/latex]) approach the number [latex]a[/latex], then we say that [latex]L[/latex] is the limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]a[/latex] from the right. Symbolically, we express this idea as
Evaluating One-Sided Limits
For the function [latex]f(x)=\begin{cases} x+1, & \text{if} \, x < 2 \\ x^2-4, & \text{if} \, x \ge 2 \end{cases}[/latex], evaluate each of the following limits.
- [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
Answer:
We can use tables of functional values again (Figure). Observe that for values of [latex]x[/latex] less than 2, we use [latex]f(x)=x+1[/latex] and for values of [latex]x[/latex] greater than 2, we use [latex]f(x)=x^2-4[/latex].
| [latex]x[/latex] | [latex]f(x)=x+1[/latex] | [latex]x[/latex] | [latex]f(x)=x^2-4[/latex] | |
|---|---|---|---|---|
| 1.9 | 2.9 | 2.1 | 0.41 | |
| 1.99 | 2.99 | 2.01 | 0.0401 | |
| 1.999 | 2.999 | 2.001 | 0.004001 | |
| 1.9999 | 2.9999 | 2.0001 | 0.00040001 | |
| 1.99999 | 2.99999 | 2.00001 | 0.0000400001 |
Based on this table, we can conclude that a. [latex]\underset{x\to 2^-}{\lim}f(x)=3[/latex] and b. [latex]\underset{x\to 2^+}{\lim}f(x)=0[/latex]. Therefore, the (two-sided) limit of [latex]f(x)[/latex] does not exist at [latex]x=2[/latex]. (Figure) shows a graph of [latex]f(x)[/latex] and reinforces our conclusion about these limits.
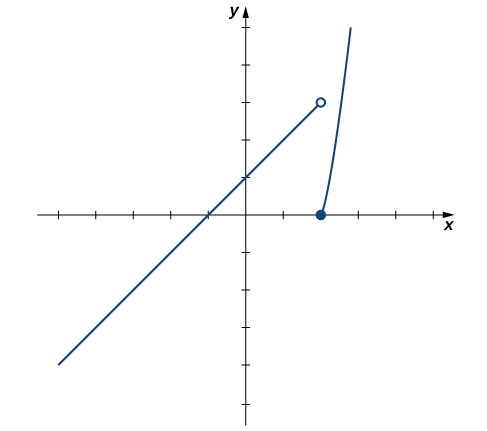 Figure 7. The graph of [latex]f(x)=\begin{cases} x+1, & \text{if} \, x < 2 \\ x^2-4, & \text{if} \, x \ge 2 \end{cases}[/latex] has a break at [latex]x=2[/latex].
Figure 7. The graph of [latex]f(x)=\begin{cases} x+1, & \text{if} \, x < 2 \\ x^2-4, & \text{if} \, x \ge 2 \end{cases}[/latex] has a break at [latex]x=2[/latex].Use a table of functional values to estimate the following limits, if possible.
- [latex]\underset{x\to 2^-}{\lim}\frac{|x^2-4|}{x-2}[/latex]
- [latex]\underset{x\to 2^+}{\lim}\frac{|x^2-4|}{x-2}[/latex]
Answer:
a. [latex]\underset{x\to 2^-}{\lim}\frac{|x^2-4|}{x-2}=-4[/latex]; b. [latex]\underset{x\to 2^+}{\lim}\frac{|x^2-4|}{x-2}=4[/latex]
Simple modifications in the limit laws allow us to apply them to one-sided limits. For example, to apply the limit laws to a limit of the form [latex]\underset{x\to a^-}{\lim}h(x)[/latex], we require the function [latex]h(x)[/latex] to be defined over an open interval of the form [latex](b,a)[/latex]; for a limit of the form [latex]\underset{x\to a^+}{\lim}h(x)[/latex], we require the function [latex]h(x)[/latex] to be defined over an open interval of the form [latex](a,c)[/latex]. (Figure) illustrates this point.
Evaluating a One-Sided Limit Using the Limit Laws
Evaluate each of the following limits, if possible.
- [latex]\underset{x\to 3^-}{\lim}\sqrt{x-3}[/latex]
- [latex]\underset{x\to 3^+}{\lim}\sqrt{x-3}[/latex]
Answer:
(Figure) illustrates the function [latex]f(x)=\sqrt{x-3}[/latex] and aids in our understanding of these limits.
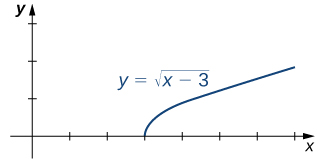 Figure 2. The graph shows the function [latex]f(x)=\sqrt{x-3}[/latex].
Figure 2. The graph shows the function [latex]f(x)=\sqrt{x-3}[/latex].- The function [latex]f(x)=\sqrt{x-3}[/latex] is defined over the interval [latex][3,+\infty)[/latex]. Since this function is not defined to the left of 3, we cannot apply the limit laws to compute [latex]\underset{x\to 3^-}{\lim}\sqrt{x-3}[/latex]. In fact, since [latex]f(x)=\sqrt{x-3}[/latex] is undefined to the left of 3, [latex]\underset{x\to 3^-}{\lim}\sqrt{x-3}[/latex] does not exist.
- Since [latex]f(x)=\sqrt{x-3}[/latex] is defined to the right of 3, the limit laws do apply to [latex]\underset{x\to 3^+}{\lim}\sqrt{x-3}[/latex]. By applying these limit laws we obtain [latex]\underset{x\to 3^+}{\lim}\sqrt{x-3}=0[/latex].
In (Figure) we look at one-sided limits of a piecewise-defined function and use these limits to draw a conclusion about a two-sided limit of the same function.
Evaluating a Two-Sided Limit Using the Limit Laws
For [latex]f(x)=\begin{cases} 4x-3 & \text{if} \, x<2 \\ (x-3)^2 & \text{if} \, x \ge 2 \end{cases}[/latex] evaluate each of the following limits:
- [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2}{\lim}f(x)[/latex]
Answer:
(Figure) illustrates the function [latex]f(x)[/latex] and aids in our understanding of these limits.
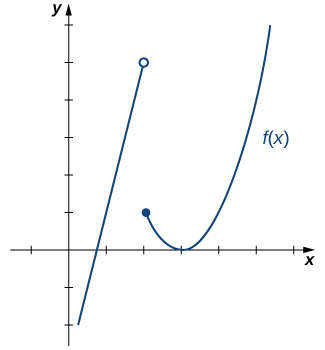 Figure 3. This graph shows the function [latex]f(x)[/latex].
Figure 3. This graph shows the function [latex]f(x)[/latex].- Since [latex]f(x)=4x-3[/latex] for all [latex]x[/latex] in [latex](−\infty,2)[/latex], replace [latex]f(x)[/latex] in the limit with [latex]4x-3[/latex] and apply the limit laws:
[latex]\underset{x\to 2^-}{\lim}f(x)=\underset{x\to 2^-}{\lim}(4x-3)=5[/latex].
- Since [latex]f(x)=(x-3)^2[/latex] for all [latex]x[/latex] in [latex](2,+\infty)[/latex], replace [latex]f(x)[/latex] in the limit with [latex](x-3)^2[/latex] and apply the limit laws:
[latex]\underset{x\to 2^+}{\lim}f(x)=\underset{x\to 2^-}{\lim}(x-3)^2=1[/latex].
- Since [latex]\underset{x\to 2^-}{\lim}f(x)=5[/latex] and [latex]\underset{x\to 2^+}{\lim}f(x)=1[/latex], we conclude that [latex]\underset{x\to 2}{\lim}f(x)[/latex] does not exist.
Graph [latex]f(x)=\begin{cases} -x-2 & \text{if} \, x<-1 \\ 2 & \text{if} \, x = -1 \\ x^3 & \text{if} \, x > -1 \end{cases}[/latex] and evaluate [latex]\underset{x\to -1^-}{\lim}f(x)[/latex].
Answer:  [latex]\underset{x\to -1^-}{\lim}f(x)=-1[/latex]
[latex]\underset{x\to -1^-}{\lim}f(x)=-1[/latex]
Hint
Use the method in (Figure) to evaluate the limit.
evaluating one-sided limits from a graph
Use the graph of [latex]f(x)[/latex] in (Figure) to determine each of the following values:
- [latex]\underset{x\to -4^-}{\lim}f(x); \, \underset{x\to -4^+}{\lim}f(x); \, \underset{x\to -4}{\lim}f(x); \, f(-4)[/latex]
- [latex]\underset{x\to -2^-}{\lim}f(x); \, \underset{x\to -2^+}{\lim}f(x); \, \underset{x\to -2}{\lim}f(x); \, f(-2)[/latex]
- [latex]\underset{x\to 1^-}{\lim}f(x); \, \underset{x\to 1^+}{\lim}f(x); \, \underset{x\to 1}{\lim}f(x); \, f(1)[/latex]
![The graph of a function f(x) described by the above limits and values. There is a smooth curve for values below x=-2; at (-2, 3), there is an open circle. There is a smooth curve between (-2, 1] with a closed circle at (1,6). There is an open circle at (1,3), and a smooth curve stretching from there down asymptotically to negative infinity along x=3. The function also curves asymptotically along x=3 on the other side, also stretching to negative infinity. The function then changes concavity in the first quadrant around y=4.5 and continues up.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11202918/CNX_Calc_Figure_02_02_015.jpg) Figure 10. The graph shows [latex]f(x)[/latex].
Figure 10. The graph shows [latex]f(x)[/latex].Answer:
Using (Figure) and the graph for reference, we arrive at the following values:
- [latex]\underset{x\to -4^-}{\lim}f(x)=0; \, \underset{x\to -4^+}{\lim}f(x)=0; \, \underset{x\to -4}{\lim}f(x)=0; \, f(-4)=0[/latex]
- [latex]\underset{x\to -2^-}{\lim}f(x)=3; \, \underset{x\to -2^+}{\lim}f(x)=3; \, \underset{x\to -2}{\lim}f(x)=3; \, f(-2)[/latex] is undefined
- [latex]\underset{x\to 1^-}{\lim}f(x)=6; \, \underset{x\to 1^+}{\lim}f(x)=3; \, \underset{x\to 1}{\lim}f(x)=DNE[/latex]; [latex]f(1)=6[/latex]
We will now recall the Squeeze Theorem to prove two special limits. The first of these limits is [latex]\underset{\theta \to 0}{\lim} \sin \theta[/latex]. Consider the unit circle shown in (Figure). In the figure, we see that [latex] \sin \theta [/latex] is the [latex]y[/latex]-coordinate on the unit circle and it corresponds to the line segment shown in blue. The radian measure of angle θ is the length of the arc it subtends on the unit circle. Therefore, we see that for [latex]0<\theta <\frac{\pi }{2}, \, 0 < \sin \theta < \theta[/latex].
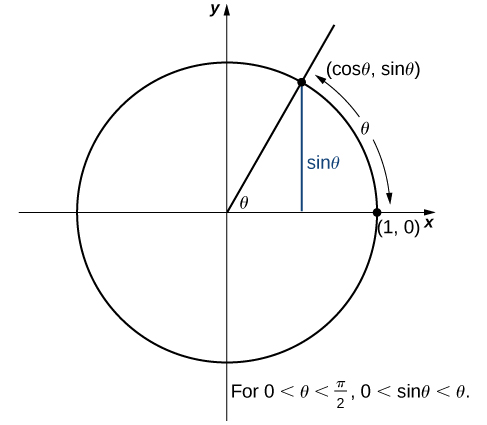 Figure 6. The sine function is shown as a line on the unit circle.
Figure 6. The sine function is shown as a line on the unit circle.Because [latex]\underset{\theta \to 0^+}{\lim}0=0[/latex] and [latex]\underset{\theta \to 0^+}{\lim}\theta =0[/latex], by using the Squeeze Theorem we conclude that
To see that [latex]\underset{\theta \to 0^-}{\lim} \sin \theta =0[/latex] as well, observe that for [latex]-\frac{\pi }{2} < \theta <0, \, 0 < −\theta < \frac{\pi}{2}[/latex] and hence, [latex]0 < \sin(-\theta) < −\theta[/latex]. Consequently, [latex]0 < -\sin \theta < −\theta[/latex] It follows that [latex]0 > \sin \theta > \theta[/latex]. An application of the Squeeze Theorem produces the desired limit. Thus, since [latex]\underset{\theta \to 0^+}{\lim} \sin \theta =0[/latex] and [latex]\underset{\theta \to 0^-}{\lim} \sin \theta =0[/latex],
Next, using the identity [latex] \cos \theta =\sqrt{1-\sin^2 \theta}[/latex] for [latex]-\frac{\pi}{2}<\theta <\frac{\pi}{2}[/latex], we see that
We now take a look at a limit that plays an important role in later chapters—namely, [latex]\underset{\theta \to 0}{\lim}\frac{\sin \theta}{\theta}[/latex]. To evaluate this limit, we use the unit circle in (Figure). Notice that this figure adds one additional triangle to (Figure). We see that the length of the side opposite angle [latex]\theta[/latex] in this new triangle is [latex]\tan \theta[/latex]. Thus, we see that for [latex]0 < \theta < \frac{\pi}{2}, \, \sin \theta < \theta < \tan \theta[/latex].
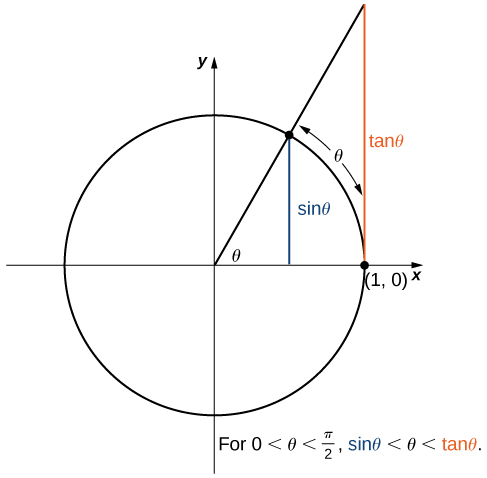 Figure 7. The sine and tangent functions are shown as lines on the unit circle.
Figure 7. The sine and tangent functions are shown as lines on the unit circle.By dividing by [latex]\sin \theta [/latex] in all parts of the inequality, we obtain
Equivalently, we have
Since [latex]\underset{\theta \to 0^+}{\lim}1=1=\underset{\theta \to 0^+}{\lim}\cos \theta[/latex], we conclude that [latex]\underset{\theta \to 0^+}{\lim}\frac{\sin \theta}{\theta}=1[/latex]. By applying a manipulation similar to that used in demonstrating that [latex]\underset{\theta \to 0^-}{\lim}\sin \theta =0[/latex], we can show that [latex]\underset{\theta \to 0^-}{\lim}\frac{\sin \theta}{\theta}=1[/latex]. Thus,
In (Figure) we use this limit to establish [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\theta}=0[/latex]. This limit also proves useful in later chapters.
Evaluating an Important Trigonometric Limit
Evaluate [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\theta}[/latex].
Answer:
In the first step, we multiply by the conjugate so that we can use a trigonometric identity to convert the cosine in the numerator to a sine:
Therefore,
Evaluate [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\sin \theta}[/latex].
Answer:
0
Hint
Multiply numerator and denominator by [latex]1+ \cos \theta[/latex].
Special Trigonometric Limits
Summarizing our work from above we have two special limits: [latex]\underset{\theta \to 0}{\lim}\frac{\sin \theta}{\theta}=1[/latex] and [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\theta}=0[/latex]Evaluating a Limit involving [latex]\frac{\sin \theta}{\theta}[/latex] and [latex]\frac{1-\cos\theta}{\theta}[/latex]
Evaluate [latex]\underset{\theta \to 0}{\lim}\frac{\sin 3\theta}{2\theta}[/latex].
Answer:
In the first step, we multiply by a power of one:
Therefore,
Evaluate [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos 3\theta}{9\theta}[/latex].
Answer:
0
Hint
Divide the numerator and denominator by [latex]3[/latex].
Key Equations
- One-Sided Limits [latex-display]\underset{x\to a^-}{\lim}f(x)=L[/latex-display] [latex]\underset{x\to a^+}{\lim}f(x)=L[/latex]
- Important Limits [latex-display]\underset{\theta \to 0}{\lim}\frac{\sin \theta}{\theta}=1[/latex-display] [latex]\underset{\theta \to 0}{\lim}\frac{1- \cos \theta}{\theta}=0[/latex]
In the following exercises, set up a table of values to find the indicated limit. Round to eight digits.
1. [T] [latex]\underset{t\to 0^+}{\lim}\frac{\cos t}{t}[/latex]
| [latex]t[/latex] | [latex]\frac{\cos t}{t}[/latex] |
|---|---|
| 0.1 | a. |
| 0.01 | b. |
| 0.001 | c. |
| 0.0001 | d. |
2. [T] [latex]\underset{x\to 2^-}{\lim}\frac{1-\frac{2}{x}}{x^2-4}[/latex]
| [latex]x[/latex] | [latex]\frac{1-\frac{2}{x}}{x^2-4}[/latex] | [latex]x[/latex] | [latex]\frac{1-\frac{2}{x}}{x^2-4}[/latex] |
|---|---|---|---|
| 1.9 | a. | 2.1 | e. |
| 1.99 | b. | 2.01 | f. |
| 1.999 | c. | 2.001 | g. |
| 1.9999 | d. | 2.0001 | h. |
Answer:
a. 0.13495277; b. 0.12594300; c. 0.12509381; d. 0.12500938; e. 0.11614402; f. 0.12406794; g. 0.12490631; h. 0.12499063;
[latex-display]\underset{x\to 2^-}{\lim}\frac{1-\frac{2}{x}}{x^2-4}=0.1250=\frac{1}{8}[/latex-display]In the following exercises, set up a table of values and round to eight significant digits. Based on the table of values, make a guess about what the limit is. Then, use a calculator to graph the function and determine the limit. Was the conjecture correct? If not, why does the method of tables fail?
3. [T] [latex]\underset{\theta \to 0^-}{\lim}\sin (\frac{\pi }{\theta })[/latex]
| θ | [latex] \sin (\frac{\pi }{\theta })[/latex] | θ | [latex] \sin (\frac{\pi }{\theta })[/latex] |
|---|---|---|---|
| −0.1 | a. | 0.1 | e. |
| −0.01 | b. | 0.01 | f. |
| −0.001 | c. | 0.001 | g. |
| −0.0001 | d. | 0.0001 | h. |
4. [T] [latex]\underset{\alpha \to 0^+}{\lim}\frac{1}{\alpha } \cos (\frac{\pi }{\alpha })[/latex]
| [latex]a[/latex] | [latex]\frac{1}{\alpha } \cos (\frac{\pi }{\alpha })[/latex] |
|---|---|
| 0.1 | a. |
| 0.01 | b. |
| 0.001 | c. |
| 0.0001 | d. |
Answer:
a. −10.00000; b. −100.00000; c. −1000.0000; d. −10,000.000; Guess: [latex]\underset{\alpha \to 0^+}{\lim}\frac{1}{\alpha } \cos (\frac{\pi }{\alpha })=\infty[/latex], Actual: DNE
![A graph of the function (1/alpha) * cos (pi / alpha), which oscillates gently until the interval [-.2, .2], where it oscillates rapidly, going to infinity and negative infinity as it approaches the y axis.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11202929/CNX_Calc_Figure_02_02_214.jpg)
In the following exercises, use direct substitution to obtain an undefined expression. Then, use the method of (Figure) to simplify the function to help determine the limit.
5. [latex]\underset{x\to 1^+}{\lim}\frac{2x^2+7x-4}{x^2+x-2}[/latex]
6. [latex]\underset{x\to -2^-}{\lim}\frac{2x^2+7x-4}{x^2+x-2}[/latex]
Answer:
[latex]-\infty[/latex]
7. [latex]\underset{x\to -2^+}{\lim}\frac{2x^2+7x-4}{x^2+x-2}[/latex]
8. [latex]\underset{x\to 1^-}{\lim}\frac{2x^2+7x-4}{x^2+x-2}[/latex]
Answer:
[latex]-\infty[/latex]
In the following exercises, use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.
9. [T] [latex]g(x)=\begin{cases} 3-x & x \le 2 \\ \frac{x}{2} & x > 2 \end{cases}[/latex]
- [latex]\underset{x\to 2^-}{\lim}g(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}g(x)[/latex]
- [latex]\underset{x\to 3^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 3^+}{\lim}f(x)[/latex]
Answer:  a. 9; b. 7
a. 9; b. 7
11. [T] [latex]g(x)=\begin{cases} x^3 - 1 & x \le 0 \\ 1 & x > 0 \end{cases}[/latex]
- [latex]\underset{x\to 0^-}{\lim}g(x)[/latex]
- [latex]\underset{x\to 0^+}{\lim}g(x)[/latex]
12. [T] [latex]h(x)=\begin{cases} x^2-2x+1 & x < 2 \\ 3 - x & x \ge 2 \end{cases}[/latex]
-
- [latex]\underset{x\to 2^-}{\lim}h(x)[/latex]
- [latex]\underset{x\to 2^+}{\lim}h(x)[/latex]
Answer:  a. 1; b. 1
a. 1; b. 1
In the following exercises, use the following graphs and the limit laws to evaluate each limit.
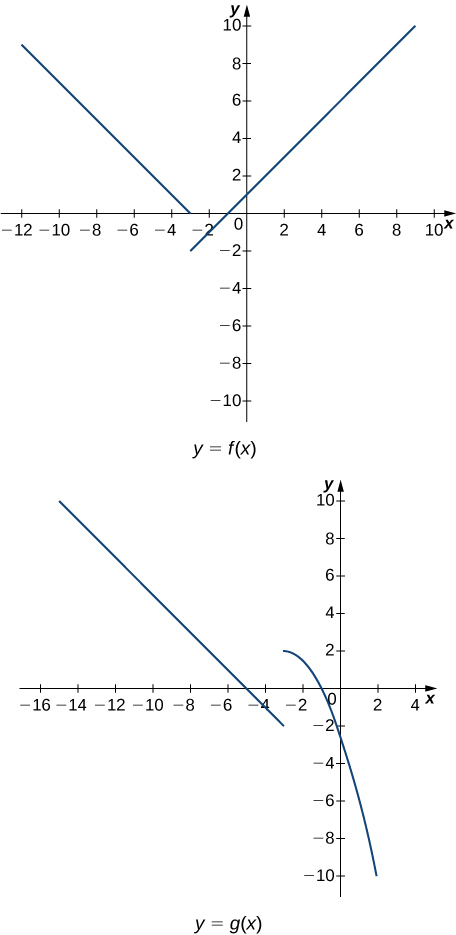
13. [latex]\underset{x\to -3^+}{\lim}(f(x)+g(x))[/latex]
14. [latex]\underset{x\to -3^-}{\lim}(f(x)-3g(x))[/latex]
Answer:
[latex]\underset{x\to -3^-}{\lim}(f(x)-3g(x))=\underset{x\to -3^-}{\lim}f(x)-3\underset{x\to -3^-}{\lim}g(x)=0+6=6[/latex]
In the following exercises, consider the graph of the function [latex]y=f(x)[/latex] shown here. Which of the statements about [latex]y=f(x)[/latex] are true and which are false? Explain why a statement is false.
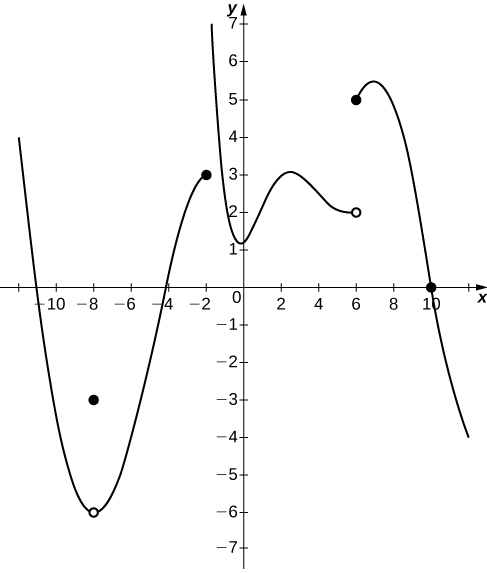
15. [latex]\underset{x\to 10^-}{\lim}f(x)=0[/latex]
16. [latex]\underset{x\to -2^+}{\lim}f(x)=3[/latex]
Answer:
False; [latex]\underset{x\to -2^+}{\lim}f(x)=+\infty [/latex]
17. [latex]\underset{x\to -8^+}{\lim}f(x)=f(-8)[/latex]
18. [latex]\underset{x\to 6}{\lim}f(x)=5[/latex]
Answer:
False; [latex]\underset{x\to 6}{\lim}f(x)[/latex] DNE since [latex]\underset{x\to 6^-}{\lim}f(x)=2[/latex] and [latex]\underset{x\to 6^+}{\lim}f(x)=5[/latex].
In the following exercises, use the following graph of the function [latex]y=f(x)[/latex] to find the values, if possible. Estimate when necessary.
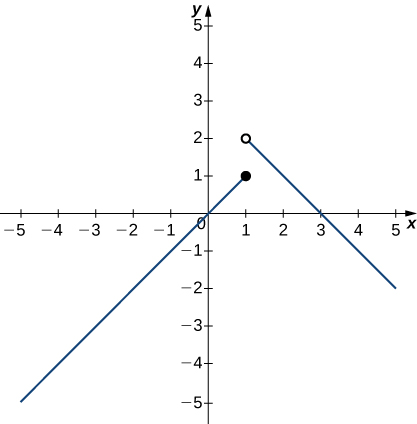
19. [latex]\underset{x\to 1^-}{\lim}f(x)[/latex]
Answer:
2
21. [latex]\underset{x\to 1}{\lim}f(x)[/latex]
In the following exercises, use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.
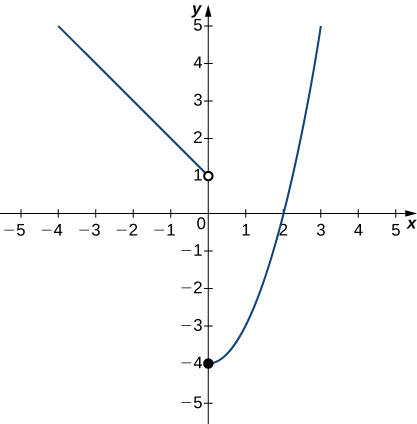
22. [latex]\underset{x\to 0^-}{\lim}f(x)[/latex]
Answer:
1
23. [latex]\underset{x\to 0^+}{\lim}f(x)[/latex]
24. [latex]\underset{x\to 2}{\lim}f(x)[/latex]
Answer:
DNE
25. [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
In the following exercises, use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.
![A graph of a piecewise function with three segments, all linear. The first exists for x < -2, has a slope of 1, and ends at the open circle at (-2, 0). The second exists over the interval [-2, 2], has a slope of -1, goes through the origin, and has closed circles at its endpoints (-2, 2) and (2,-2). The third exists for x>2, has a slope of 1, and begins at the open circle (2,2).](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11202943/CNX_Calc_Figure_02_02_204.jpg)
26. [latex]\underset{x\to -2^-}{\lim}f(x)[/latex]
Answer:
0
27. [latex]\underset{x\to -2^+}{\lim}f(x)[/latex]
28. [latex]\underset{x\to -2}{\lim}f(x)[/latex]
Answer:
DNE
29. [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]
30. [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
Answer:
2
31. [latex]\underset{x\to 2}{\lim}f(x)[/latex]
In the following exercises, use the graph of the function [latex]y=g(x)[/latex] shown here to find the values, if possible. Estimate when necessary.
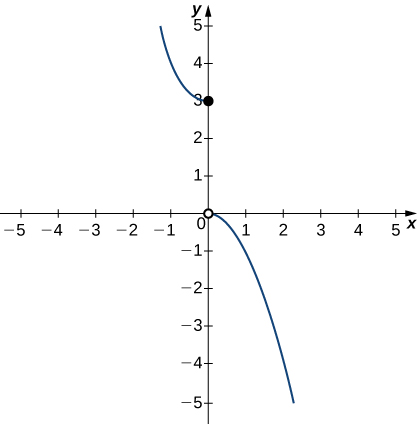
32. [latex]\underset{x\to 0^-}{\lim}g(x)[/latex]
Answer:
3
33. [latex]\underset{x\to 0^+}{\lim}g(x)[/latex]
34. [latex]\underset{x\to 0}{\lim}g(x)[/latex]
Answer:
DNE
In the following exercises, use the graph of the function [latex]y=h(x)[/latex] shown here to find the values, if possible. Estimate when necessary.
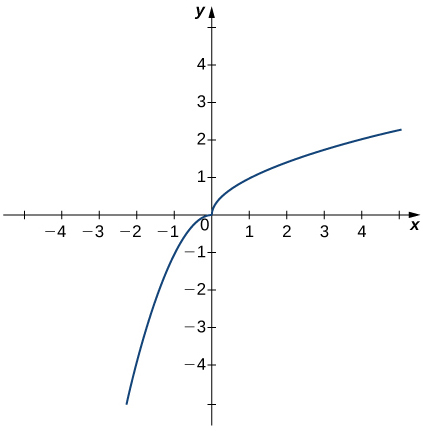
35. [latex]\underset{x\to 0^-}{\lim}h(x)[/latex]
36. [latex]\underset{x\to 0^+}{\lim}h(x)[/latex]
Answer:
0
37. [latex]\underset{x\to 0}{\lim}h(x)[/latex]
In the following exercises, use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.
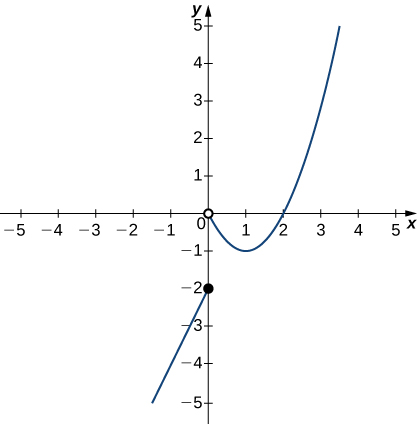
38. [latex]\underset{x\to 0^-}{\lim}f(x)[/latex]
Answer:
−2
39. [latex]\underset{x\to 0^+}{\lim}f(x)[/latex]
40. [latex]\underset{x\to 0}{\lim}f(x)[/latex]
Answer:
DNE
41. [latex]\underset{x\to 1^-}{\lim}f(x)[/latex]
42. [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]
Answer:
0
43. [latex]\underset{\theta \to 0}{\lim}\frac{\sin 2\theta}{5\theta}[/latex]
44. [latex]\underset{\theta \to 0}{\lim}\frac{\sin 4\theta}{3\theta}[/latex]
Answer:
[latex]\frac{4}{3}[/latex]
45. [latex]\underset{\theta \to 0}{\lim}\frac{1-\cos 2\theta}{9\theta}[/latex]
46. [latex]\underset{\theta \to 0}{\lim}\frac{1-\cos 2\theta}{3\theta}[/latex]
Answer:
[latex]0[/latex]
47. [latex]\underset{\theta \to 0}{\lim}\frac{\cos 2\theta+\sin 5\theta-1}{2\theta}[/latex]
48. [latex]\underset{\theta \to 0}{\lim}\frac{\cos 7\theta+\sin 2\theta-1}{7\theta}[/latex]
Answer:
[latex]\frac{2}{7}[/latex]
49. [latex]\underset{x \to 0}{\lim}\frac{x^2-x-\sin x}{3x}[/latex]
50. [latex]\underset{x \to 0}{\lim}\frac{x^2+x+\sin x}{4x}[/latex]
Answer:
[latex]\frac{1}{2}[/latex]
51. [latex]\underset{x \to 0}{\lim}\frac{\sin 5x}{\sin 4x}[/latex]
52. [latex]\underset{x \to 0}{\lim}\frac{\sin x}{\sin 2x}[/latex]
Answer:
[latex]\frac{1}{2}[/latex]

Hint