We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Calculus Volume 1

The First Derivative Test

Learning Objectives

  • Explain how the sign of the first derivative affects the shape of a function’s graph.
  • State the first derivative test for critical points.
  • Find local extrema using the first derivative test.

Earlier in this chapter we stated that if a function [latex]f[/latex] has a local extremum at a point [latex]c[/latex], then [latex]c[/latex] must be a critical point of [latex]f[/latex]. However, a function is not guaranteed to have a local extremum at a critical point. For example, [latex]f(x)=x^3[/latex] has a critical point at [latex]x=0[/latex] since [latex]f^{\prime}(x)=3x^2[/latex] is zero at [latex]x=0[/latex], but [latex]f[/latex] does not have a local extremum at [latex]x=0[/latex]. Using the results from the previous section, we are now able to determine whether a critical point of a function actually corresponds to a local extreme value. In this section, we also see how the second derivative provides information about the shape of a graph by describing whether the graph of a function curves upward or curves downward.

The First Derivative Test

Corollary 3 of the Mean Value Theorem showed that if the derivative of a function is positive over an interval [latex]I[/latex] then the function is increasing over [latex]I[/latex]. On the other hand, if the derivative of the function is negative over an interval [latex]I[/latex], then the function is decreasing over [latex]I[/latex] as shown in the following figure.

This figure is broken into four figures labeled a, b, c, and d. Figure a shows a function increasing convexly from (a, f(a)) to (b, f(b)). At two points the derivative is taken and it is noted that at both f’ > 0. In other words, f is increasing. Figure b shows a function increasing concavely from (a, f(a)) to (b, f(b)). At two points the derivative is taken and it is noted that at both f’ > 0. In other words, f is increasing. Figure c shows a function decreasing concavely from (a, f(a)) to (b, f(b)). At two points the derivative is taken and it is noted that at both f’ < 0. In other words, f is decreasing. Figure d shows a function decreasing convexly from (a, f(a)) to (b, f(b)). At two points the derivative is taken and it is noted that at both f’ < 0. In other words, f is decreasing. Figure 1. Both functions are increasing over the interval [latex](a,b)[/latex]. At each point [latex]x[/latex], the derivative [latex]f^{\prime}(x)>0[/latex]. Both functions are decreasing over the interval [latex](a,b)[/latex]. At each point [latex]x[/latex], the derivative [latex]f^{\prime}(x)<0[/latex].

A continuous function [latex]f[/latex] has a local maximum at point [latex]c[/latex] if and only if [latex]f[/latex] switches from increasing to decreasing at point [latex]c[/latex]. Similarly, [latex]f[/latex] has a local minimum at [latex]c[/latex] if and only if [latex]f[/latex] switches from decreasing to increasing at [latex]c[/latex]. If [latex]f[/latex] is a continuous function over an interval [latex]I[/latex] containing [latex]c[/latex] and differentiable over [latex]I[/latex], except possibly at [latex]c[/latex], the only way [latex]f[/latex] can switch from increasing to decreasing (or vice versa) at point [latex]c[/latex] is if [latex]{f}^{\prime }[/latex] changes sign as [latex]x[/latex] increases through [latex]c.[/latex] If [latex]f[/latex] is differentiable at [latex]c,[/latex] the only way that [latex]{f}^{\prime }.[/latex] can change sign as [latex]x[/latex] increases through [latex]c[/latex] is if [latex]f^{\prime}(c)=0[/latex]. Therefore, for a function [latex]f[/latex] that is continuous over an interval [latex]I[/latex] containing [latex]c[/latex] and differentiable over [latex]I[/latex], except possibly at [latex]c[/latex], the only way [latex]f[/latex] can switch from increasing to decreasing (or vice versa) is if [latex]f^{\prime}(c)=0[/latex] or [latex]f^{\prime}(c)[/latex] is undefined. Consequently, to locate local extrema for a function [latex]f[/latex], we look for points [latex]c[/latex] in the domain of [latex]f[/latex] such that [latex]f^{\prime}(c)=0[/latex] or [latex]f^{\prime}(c)[/latex] is undefined. Recall that such points are called critical points of [latex]f[/latex].

Note that [latex]f[/latex] need not have a local extrema at a critical point. The critical points are candidates for local extrema only. In (Figure), we show that if a continuous function [latex]f[/latex] has a local extremum, it must occur at a critical point, but a function may not have a local extremum at a critical point. We show that if [latex]f[/latex] has a local extremum at a critical point, then the sign of [latex]f^{\prime}[/latex] switches as [latex]x[/latex] increases through that point.
A function f(x) is graphed. It starts in the second quadrant and increases to x = a, which is too sharp and hence f’(a) is undefined. In this section f’ > 0. Then, f decreases from x = a to x = b (so f’ < 0 here), before increasing at x = b. It is noted that f’(b) = 0. While increasing from x = b to x = c, f’ > 0. The function has an inversion point at c, and it is marked f’(c) = 0. The function increases some more to d (so f’ > 0), which is the global maximum. It is marked that f’(d) = 0. Then the function decreases and it is marked that f’ > 0. Figure 2. The function [latex]f[/latex] has four critical points: [latex]a,b,c[/latex], and [latex]d[/latex]. The function [latex]f[/latex] has local maxima at [latex]a[/latex] and [latex]d[/latex], and a local minimum at [latex]b[/latex]. The function [latex]f[/latex] does not have a local extremum at [latex]c[/latex]. The sign of [latex]f^{\prime}[/latex] changes at all local extrema.

Using (Figure), we summarize the main results regarding local extrema.

  • If a continuous function [latex]f[/latex] has a local extremum, it must occur at a critical point [latex]c[/latex].
  • The function has a local extremum at the critical point [latex]c[/latex] if and only if the derivative [latex]f^{\prime}[/latex] switches sign as [latex]x[/latex] increases through [latex]c[/latex].
  • Therefore, to test whether a function has a local extremum at a critical point [latex]c[/latex], we must determine the sign of [latex]f^{\prime}(x)[/latex] to the left and right of [latex]c[/latex].

This result is known as the first derivative test.

First Derivative Test

Suppose that [latex]f[/latex] is a continuous function over an interval [latex]I[/latex] containing a critical point [latex]c[/latex]. If [latex]f[/latex] is differentiable over [latex]I[/latex], except possibly at point [latex]c[/latex], then [latex]f(c)[/latex] satisfies one of the following descriptions:

  1. If [latex]f^{\prime}[/latex] changes sign from positive when [latex]x<c[/latex] to negative when [latex]x>c[/latex], then [latex]f(c)[/latex] is a local maximum of [latex]f[/latex].
  2. If [latex]f^{\prime}[/latex] changes sign from negative when [latex]x<c[/latex] to positive when [latex]x>c[/latex], then [latex]f(c)[/latex] is a local minimum of [latex]f[/latex].
  3. If [latex]f^{\prime}[/latex] has the same sign for [latex]x<c[/latex] and [latex]x>c[/latex], then [latex]f(c)[/latex] is neither a local maximum nor a local minimum of [latex]f[/latex].

We can summarize the first derivative test as a strategy for locating local extrema.

Problem-Solving Strategy: Using the First Derivative Test

Consider a function [latex]f[/latex] that is continuous over an interval [latex]I[/latex].

  1. Find all critical points of [latex]f[/latex] and divide the interval [latex]I[/latex] into smaller intervals using the critical points as endpoints.
  2. Analyze the sign of [latex]f^{\prime}[/latex] in each of the subintervals. If [latex]f^{\prime}[/latex] is continuous over a given subinterval (which is typically the case), then the sign of [latex]f^{\prime}[/latex] in that subinterval does not change and, therefore, can be determined by choosing an arbitrary test point [latex]x[/latex] in that subinterval and by evaluating the sign of [latex]f^{\prime}[/latex] at that test point. Use the sign analysis to determine whether [latex]f[/latex] is increasing or decreasing over that interval.
  3. Use (Figure) and the results of step 2 to determine whether [latex]f[/latex] has a local maximum, a local minimum, or neither at each of the critical points.
Now let’s look at how to use this strategy to locate all local extrema for particular functions.

Using the First Derivative Test to Find Local Extrema

Use the first derivative test to find the location of all local extrema for [latex]f(x)=x^3-3x^2-9x-1[/latex]. Use a graphing utility to confirm your results.

Answer:

Step 1. The derivative is [latex]f^{\prime}(x)=3x^2-6x-9[/latex]. To find the critical points, we need to find where [latex]f^{\prime}(x)=0[/latex]. Factoring the polynomial, we conclude that the critical points must satisfy

[latex]3(x^2-2x-3)=3(x-3)(x+1)=0[/latex].

Therefore, the critical points are [latex]x=3,-1[/latex]. Now divide the interval [latex](−\infty ,\infty)[/latex] into the smaller intervals [latex](−\infty ,-1), \, (-1,3)[/latex], and [latex](3,\infty)[/latex].

Step 2. Since [latex]f^{\prime}[/latex] is a continuous function, to determine the sign of [latex]f^{\prime}(x)[/latex] over each subinterval, it suffices to choose a point over each of the intervals [latex](−\infty ,-1), \, (-1,3)[/latex], and [latex](3,\infty)[/latex] and determine the sign of [latex]f^{\prime}[/latex] at each of these points. For example, let’s choose [latex]x=-2, \, x=0[/latex], and [latex]x=4[/latex] as test points.

Interval Test Point Sign of [latex]f^{\prime}(x)=3(x-3)(x+1)[/latex] at Test Point Conclusion
[latex](−\infty ,-1)[/latex] [latex]x=-2[/latex] [latex](+)(−)(−)=+[/latex] [latex]f[/latex] is increasing.
[latex](-1,3)[/latex] [latex]x=0[/latex] [latex](+)(−)(+)=−[/latex] [latex]f[/latex] is decreasing.
[latex](3,\infty)[/latex] [latex]x=4[/latex] [latex](+)(+)(+)=+[/latex] [latex]f[/latex] is increasing.

Step 3. Since [latex]f^{\prime}[/latex] switches sign from positive to negative as [latex]x[/latex] increases through [latex]1, \, f[/latex] has a local maximum at [latex]x=-1[/latex]. Since [latex]f^{\prime}[/latex] switches sign from negative to positive as [latex]x[/latex] increases through [latex]3, \, f[/latex] has a local minimum at [latex]x=3[/latex]. These analytical results agree with the following graph.

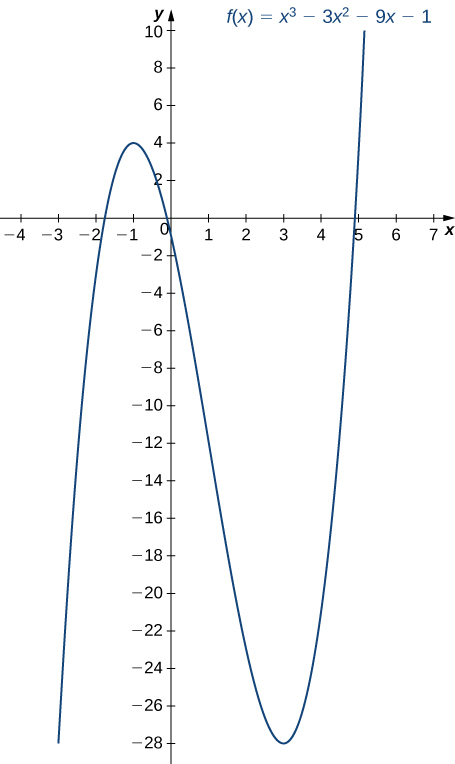The function f(x) = x3 – 3x2 – 9x – 1 is graphed. It has a maximum at x = −1 and a minimum at x = 3. The function is increasing before x = −1, decreasing until x = 3, and then increasing after that. Figure 3. The function [latex]f[/latex] has a maximum at [latex]x=-1[/latex] and a minimum at [latex]x=3[/latex]

Use the first derivative test to locate all local extrema for [latex]f(x)=−x^3+\frac{3}{2}x^2+18x[/latex].

Answer:

[latex]f[/latex] has a local minimum at -2 and a local maximum at 3.

Hint

Find all critical points of [latex]f[/latex] and determine the signs of [latex]f^{\prime}(x)[/latex] over particular intervals determined by the critical points.

Using the First Derivative Test

Use the first derivative test to find the location of all local extrema for [latex]f(x)=5x^{1/3}-x^{5/3}[/latex]. Use a graphing utility to confirm your results.

Answer:

Step 1. The derivative is

[latex]f^{\prime}(x)=\frac{5}{3}x^{-2/3}-\frac{5}{3}x^{2/3}=\frac{5}{3x^{2/3}}-\frac{5x^{2/3}}{3}=\frac{5-5x^{4/3}}{3x^{2/3}}=\frac{5(1-x^{4/3})}{3x^{2/3}}[/latex].
The derivative [latex]f^{\prime}(x)=0[/latex] when [latex]1-x^{4/3}=0[/latex]. Therefore, [latex]f^{\prime}(x)=0[/latex] at [latex]x=\pm 1[/latex]. The derivative [latex]f^{\prime}(x)[/latex] is undefined at [latex]x=0[/latex]. Therefore, we have three critical points: [latex]x=0[/latex], [latex]x=1[/latex], and [latex]x=-1[/latex]. Consequently, divide the interval [latex](−\infty ,\infty)[/latex] into the smaller intervals [latex](−\infty ,-1), \, (-1,0), \, (0,1)[/latex], and [latex](1,\infty )[/latex].

Step 2: Since [latex]f^{\prime}[/latex] is continuous over each subinterval, it suffices to choose a test point [latex]x[/latex] in each of the intervals from step 1 and determine the sign of [latex]f^{\prime}[/latex] at each of these points. The points [latex]x=-2, \, x=-\frac{1}{2}, \, x=\frac{1}{2}[/latex], and [latex]x=2[/latex] are test points for these intervals.

Interval Test Point Sign of [latex]f^{\prime}(x)=\frac{5(1-x^{4/3})}{3x^{2/3}}[/latex] at Test Point Conclusion
[latex](−\infty ,-1)[/latex] [latex]x=-2[/latex] [latex]\frac{(+)(−)}{+}=−[/latex] [latex]f[/latex] is decreasing.
[latex](-1,0)[/latex] [latex]x=-\frac{1}{2}[/latex] [latex]\frac{(+)(+)}{+}=+[/latex] [latex]f[/latex] is increasing.
[latex](0,1)[/latex] [latex]x=\frac{1}{2}[/latex] [latex]\frac{(+)(+)}{+}=+[/latex] [latex]f[/latex] is increasing.
[latex](1,\infty )[/latex] [latex]x=2[/latex] [latex]\frac{(+)(−)}{+}=−[/latex] [latex]f[/latex] is decreasing.

Step 3: Since [latex]f[/latex] is decreasing over the interval [latex](−\infty ,-1)[/latex] and increasing over the interval [latex](-1,0)[/latex], [latex]f[/latex] has a local minimum at [latex]x=-1[/latex]. Since [latex]f[/latex] is increasing over the interval [latex](-1,0)[/latex] and the interval [latex](0,1)[/latex], [latex]f[/latex] does not have a local extremum at [latex]x=0[/latex]. Since [latex]f[/latex] is increasing over the interval [latex](0,1)[/latex] and decreasing over the interval [latex](1,\infty ), \, f[/latex] has a local maximum at [latex]x=1[/latex]. The analytical results agree with the following graph.

The function f(x) = 5x1/3 – x5/3 is graphed. It decreases to its local minimum at x = −1, increases to x = 1, and then decreases after that. Figure 4. The function f has a local minimum at [latex]x=-1[/latex] and a local maximum at [latex]x=1[/latex].

Use the first derivative test to find all local extrema for [latex]f(x)=\sqrt[3]{x-1}[/latex].

Answer:

[latex]f[/latex] has no local extrema because [latex]f^{\prime}[/latex] does not change sign at [latex]x=1[/latex].

Hint

The only critical point of [latex]f[/latex] is [latex]x=1[/latex].

Key Concepts

  • If [latex]c[/latex] is a critical point of [latex]f[/latex] and [latex]f^{\prime}(x)>0[/latex] for [latex]x<c[/latex] and [latex]f^{\prime}(x)<0[/latex] for [latex]x>c[/latex], then [latex]f[/latex] has a local maximum at [latex]c[/latex].
  • If [latex]c[/latex] is a critical point of [latex]f[/latex] and [latex]f^{\prime}(x)<0[/latex] for [latex]x<c[/latex] and [latex]f^{\prime}(x)>0[/latex] for [latex]x>c[/latex], then [latex]f[/latex] has a local minimum at [latex]c[/latex].

1. If [latex]c[/latex] is a critical point of [latex]f(x)[/latex], when is there no local maximum or minimum at [latex]c[/latex]? Explain.

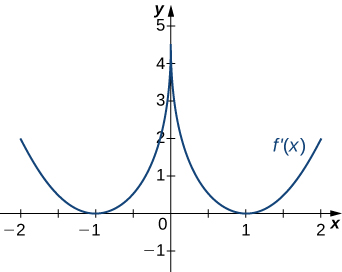
For the following exercises, analyze the graphs of [latex]f^{\prime}[/latex], then list all intervals where [latex]f[/latex] is increasing or decreasing.

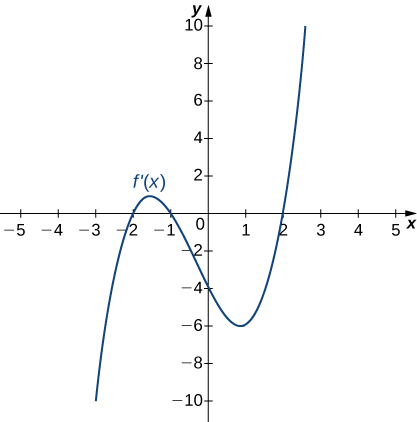
2. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−2, 0). Then it continues increasing a little before decreasing and crossing the x axis at (−1, 0). It achieves a local minimum at (1, −6) before increasing and crossing the x axis at (2, 0).

Answer:

Increasing for [latex]-2<x<-1[/latex] and [latex]x>2[/latex]; decreasing for [latex]x<-2[/latex] and [latex]-1<x<2[/latex]

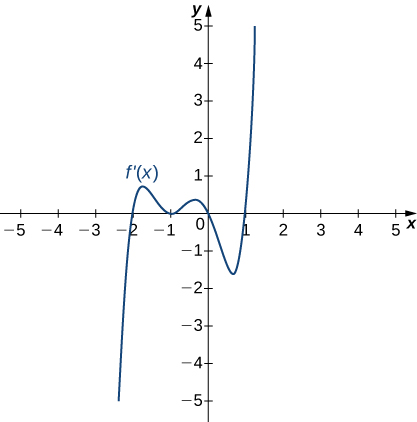
3. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−2, 0). Then it continues increasing a little before decreasing and touching the x axis at (−1, 0). It then increases a little before decreasing and crossing the x axis at the origin. The function then decreases to a local minimum before increasing, crossing the x-axis at (1, 0), and continuing to increase.
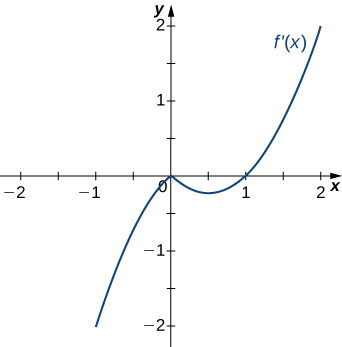
4. The function f’(x) is graphed. The function starts negative and touches the x axis at the origin. Then it decreases a little before increasing to cross the x axis at (1, 0) and continuing to increase.

Answer:

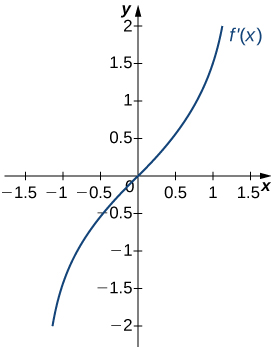
Decreasing for [latex]x<1[/latex]; increasing for [latex]x>1[/latex]

5. The function f’(x) is graphed. The function starts positive and decreases to touch the x axis at (−1, 0). Then it increases to (0, 4.5) before decreasing to touch the x axis at (1, 0). Then the function increases.
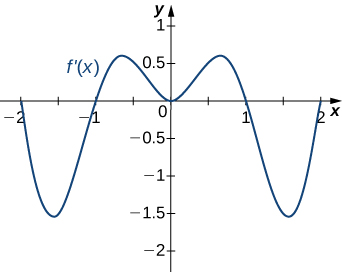
6. The function f’(x) is graphed. The function starts at (−2, 0), decreases to (−1.5, −1.5), increases to (−1, 0), and continues increasing before decreasing to the origin. Then the other side is symmetric: that is, the function increases and then decreases to pass through (1, 0). It continues decreasing to (1.5, −1.5), and then increase to (2, 0).

Answer:

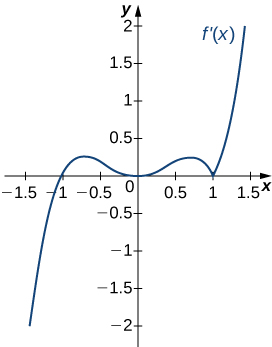
Decreasing for [latex]-2<x<-1[/latex] and [latex]1<x<2[/latex]; increasing for [latex]-1<x<1[/latex] and [latex]x<-2[/latex] and [latex]x>2[/latex]

For the following exercises, analyze the graphs of [latex]f^{\prime}[/latex], then list

  1. all intervals where [latex]f[/latex] is increasing and decreasing and
  2. where the minima and maxima are located.
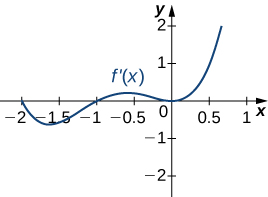
7. The function f’(x) is graphed. The function starts at (−2, 0), decreases for a little and then increases to (−1, 0), continues increasing before decreasing to the origin, at which point it increases.
8. The function f’(x) is graphed. The function starts at (−2, 0), increases and then decreases to (−1, 0), decreases and then increases to an inflection point at the origin. Then the function increases and decreases to cross (1, 0). It continues decreasing and then increases to (2, 0).

Answer:

a. Increasing over [latex]-2<x<-1, \, 0<x<1, \, x>2[/latex]; decreasing over [latex]x<-2 \, -1<x<0, \, 1<x<2[/latex]; b. maxima at [latex]x=-1[/latex] and [latex]x=1[/latex], minima at [latex]x=-2[/latex] and [latex]x=0[/latex] and [latex]x=2[/latex]

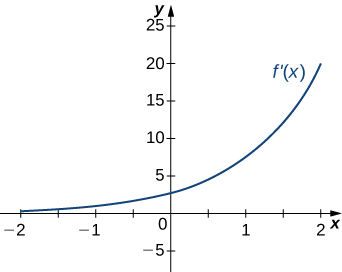
9. The function f’(x) is graphed from x = −2 to x = 2. It starts near zero at x = −2, but then increases rapidly and remains positive for the entire length of the graph.
10. The function f’(x) is graphed. The function starts negative and crosses the x axis at the origin, which is an inflection point. Then it continues increasing.

Answer:

a. Increasing over [latex]x>0[/latex], decreasing over [latex]x<0[/latex]; b. Minimum at [latex]x=0[/latex]

11. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−1, 0). Then it continues increasing a little before decreasing and touching the x axis at the origin. It increases again and then decreases to (1, 0). Then it increases.

For the following exercises, determine

  1. intervals where [latex]f[/latex] is increasing or decreasing (in interval notation) and
  2. local minima and maxima (as a coordinate).

12. [latex]f(x)=-x^2-3x+3[/latex]

Answer:

a. Increasing: [latex]\left(\infty,-\frac{3}{2}\right)[/latex], decreasing: [latex]\left(-\frac{3}{2},\infty\right)[/latex] b. Local maximum at [latex]x=-\frac{3}{2}[/latex]; no local minimum.

13. [latex]f(x)=6x-x^3[/latex]

14. [latex]f(x)=3x^2-4x^3[/latex]

Answer:

a. Increasing: [latex]\left(0,\frac{1}{2}\right)[/latex], decreasing: [latex]\left(-\infty,0\right)\cup\left(\frac{1}{2},\infty\right)[/latex] b. Local maximum at [latex]\left(\frac{1}{2},\frac{1}{4}\right)[/latex]; local minimum at [latex](0,0)[/latex].

15. [latex]g(t)=t^4-4t^3+4t^2[/latex]

16. [latex]f(t)=t^4-8t^2+16[/latex]

Answer:

a. Increasing: [latex]\left(-2,0\right)\cup\left(2,\infty\right)[/latex], decreasing: [latex]\left(-\infty,-2\right)\cup\left(0,2\right)[/latex] b. Local maximum at [latex](0,16)[/latex]; local minimums at [latex](-2,0)[/latex] and [latex](2,0)[/latex].

17. [latex]h(x)=4\sqrt{x}-x^2+3[/latex]

18. [latex]h(x)=x-6\sqrt{x-1}[/latex]

Answer:

a. Increasing: [latex]\left(10,\infty\right)[/latex], decreasing: [latex]\left(1,10\right)[/latex] b. No local maximum; local minimum at [latex](10,-8)[/latex].

19. [latex]g(x)=x^{2}\sqrt{5-x}[/latex]

20. [latex]g(x)=x\sqrt{8-x^{2}}[/latex]

Answer:

a. Increasing: [latex]\left(-2,2\right)[/latex], decreasing: [latex]\left(-2\sqrt{2},-2\right)\cup\left(2,2\sqrt{2}\right)[/latex] b. local maximum at [latex]\left(2,4\right)[/latex]; local minimum at [latex]\left(-2,-4\right)[/latex].

21. [latex]f(\theta)=\theta^2 + \cos \theta[/latex]

22. [latex]f(\theta)= \sin \theta+ \sin^3 \theta[/latex] over the interval [latex]\left(-\pi,\pi\right) [/latex]

Answer:

a. Increasing: [latex]\left(-\frac{\pi }{2},\frac{\pi }{2}\right)[/latex], decreasing: [latex]\left(-\pi,-\frac{\pi}{2}\right)\cup\left(\frac{\pi}{2},\pi\right)[/latex] b. Local maximum at [latex]\left(\frac{\pi }{2},2\right)[/latex]; local minimum at [latex]\left(-\frac{\pi }{2},-2\right)[/latex]

23. [latex]f(x)=\frac{x^3}{3x^2+1}[/latex]

24. [latex]f(x)=\frac{x^2-3}{x-2}[/latex]

Answer:

a. Increasing: [latex]\left(-\infty,1\right)[/latex], decreasing: [latex](1,2)\cup(2,3)[/latex] b. local maximum at [latex](1,2)[/latex]; local minimum at [latex](3,6)[/latex].

25. [latex]h(x)=x^{\frac{2}{3}}(x+5)[/latex]

26. [latex]h(x)=x^{\frac{1}{3}}(x+8)[/latex]

Answer:

a. Increasing: [latex]\left(-2,0\right)\cup\left(0,\infty\right)[/latex], decreasing: [latex]\left(-\infty,-2\right)[/latex] b. no local maximum; local minimum at [latex]\left(-2,-6 \sqrt[3]{2}\right)[/latex].

27. [latex]f(x)=e^{\sqrt{x}}[/latex]

28. [latex]f(x)=e^{2x}+e^{-x}[/latex]

Answer:

a. Increasing: [latex]\left(-\frac{\ln(2)}{3},\infty\right)[/latex], decreasing: [latex]\left(-\infty,-\frac{\ln(2)}{3}\right)[/latex] b. no local maximum; local minimum at [latex]\left(-\frac{\ln(2)}{3}, \frac{3\sqrt[3]{2}}{2}\right)[/latex].

29. [latex]f(t)=t^{2}\ln t[/latex]

30. [latex]f(t)=8t \ln t[/latex]

Answer:

a. Increasing: [latex]\left(\frac{1}{e},\infty\right)[/latex], decreasing: [latex]\left(0,\frac{1}{e}\right)[/latex] b. no local maximum; local minimum at [latex]\left(\frac{1}{e}, -\frac{8}{e}\right)[/latex].

Glossary

concave down
if [latex]f[/latex] is differentiable over an interval [latex]I[/latex] and [latex]f^{\prime}[/latex] is decreasing over [latex]I[/latex], then [latex]f[/latex] is concave down over [latex]I[/latex]
concave up
if [latex]f[/latex] is differentiable over an interval [latex]I[/latex] and [latex]f^{\prime}[/latex] is increasing over [latex]I[/latex], then [latex]f[/latex] is concave up over [latex]I[/latex]
concavity
the upward or downward curve of the graph of a function
concavity test
suppose [latex]f[/latex] is twice differentiable over an interval [latex]I[/latex]; if [latex]f^{\prime \prime}>0[/latex] over [latex]I[/latex], then [latex]f[/latex] is concave up over [latex]I[/latex]; if [latex]f^{\prime \prime}<0[/latex] over [latex]I[/latex], then [latex]f[/latex] is concave down over [latex]I[/latex]
first derivative test
let [latex]f[/latex] be a continuous function over an interval [latex]I[/latex] containing a critical point [latex]c[/latex] such that [latex]f[/latex] is differentiable over [latex]I[/latex] except possibly at [latex]c[/latex]; if [latex]f^{\prime}[/latex] changes sign from positive to negative as [latex]x[/latex] increases through [latex]c[/latex], then [latex]f[/latex] has a local maximum at [latex]c[/latex]; if [latex]f^{\prime}[/latex] changes sign from negative to positive as [latex]x[/latex] increases through [latex]c[/latex], then [latex]f[/latex] has a local minimum at [latex]c[/latex]; if [latex]f^{\prime}[/latex] does not change sign as [latex]x[/latex] increases through [latex]c[/latex], then [latex]f[/latex] does not have a local extremum at [latex]c[/latex]
inflection point
if [latex]f[/latex] is continuous at [latex]c[/latex] and [latex]f[/latex] changes concavity at [latex]c[/latex], the point [latex](c,f(c))[/latex] is an inflection point of [latex]f[/latex]
second derivative test
suppose [latex]f^{\prime}(c)=0[/latex] and [latex]f^{\prime \prime}[/latex] is continuous over an interval containing [latex]c[/latex]; if [latex]f^{\prime \prime}(c)>0[/latex], then [latex]f[/latex] has a local minimum at [latex]c[/latex]; if [latex]f^{\prime \prime}(c)<0[/latex], then [latex]f[/latex] has a local maximum at [latex]c[/latex]; if [latex]f^{\prime \prime}(c)=0[/latex], then the test is inconclusive

Licenses & Attributions

CC licensed content, Shared previously