Characteristics of Graphs of Exponential Functions

Learning Objectives

Determine whether an exponential function and it's associated graph represents growth or decay
Sketch a graph of an exponential function

Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is greater than one. We’ll use the function [latex]f\left(x\right)={2}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
[latex]f\left(x\right)={2}^{x}[/latex]	[latex]\frac{1}{8}[/latex]	[latex]\frac{1}{4}[/latex]	[latex]\frac{1}{2}[/latex]	1	2	4	8

Each output value is the product of the previous output and the base, 2. We call the base 2 the constant ratio. In fact, for any exponential function with the form [latex]f\left(x\right)=a{b}^{x}[/latex], b is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of a. Notice from the table that

the output values are positive for all values of x;
as x increases, the output values increase without bound; and
as x decreases, the output values grow smaller, approaching zero.

The graph below shows the exponential growth function [latex]f\left(x\right)={2}^{x}[/latex].

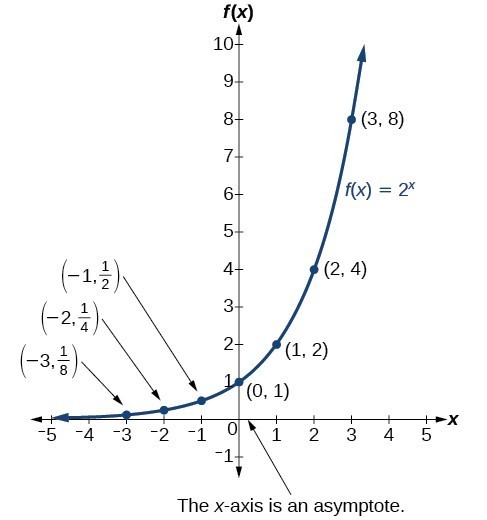Graph of the exponential function, 2^(x), with labeled points at (-3, 1/8), (-2, ¼), (-1, ½), (0, 1), (1, 2), (2, 4), and (3, 8). The graph notes that the x-axis is an asymptote.

Notice that the graph gets close to the x-axis, but never touches it.

The domain of [latex]f\left(x\right)={2}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex]. To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is between zero and one. We’ll use the function [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex]. Observe how the output values in the table below change as the input increases by 1.

x	–3	–2	–1	0	1	2	3
[latex]g\left(x\right)=\left(\frac{1}{2}\right)^{x}[/latex]	8	4	2	1	[latex]\frac{1}{2}[/latex]	[latex]\frac{1}{4}[/latex]	[latex]\frac{1}{8}[/latex]

Again, because the input is increasing by 1, each output value is the product of the previous output and the base, or constant ratio [latex]\frac{1}{2}[/latex]. Notice from the table that

the output values are positive for all values of x;
as x increases, the output values grow smaller, approaching zero; and
as x decreases, the output values grow without bound.

The graph shows the exponential decay function, [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex].

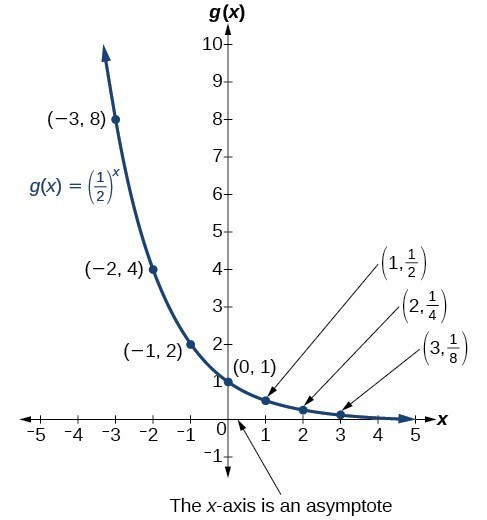Graph of decreasing exponential function, (1/2)^x, with labeled points at (-3, 8), (-2, 4), (-1, 2), (0, 1), (1, 1/2), (2, 1/4), and (3, 1/8). The graph notes that the x-axis is an asymptote.

The domain of [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].

A General Note: Characteristics of the Graph of the Parent Function f(x) = b^x

An exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], [latex]b>0[/latex], [latex]b\ne 1[/latex], has these characteristics:

one-to-one function
horizontal asymptote: [latex]y=0[/latex]
domain: [latex]\left(-\infty , \infty \right)[/latex]
range: [latex]\left(0,\infty \right)[/latex]
x-intercept: none
y-intercept: [latex]\left(0,1\right)[/latex]
increasing if [latex]b>1[/latex]
decreasing if [latex]b<1[/latex]

Use the sliders in the graph below to compare the graphs of exponential growth and decay functions. Which one is growth and which one is decay? https://www.desmos.com/calculator/3pqyjsunkg

How To: Given an exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], graph the function by hand.

Create a table of points.
Plot at least 3 point from the table, including the y-intercept [latex]\left(0,1\right)[/latex].
Draw a smooth curve through the points.
State the domain, [latex]\left(-\infty ,\infty \right)[/latex], the range, [latex]\left(0,\infty \right)[/latex], and the horizontal asymptote, [latex]y=0[/latex].

Example: Sketching the Graph of an Exponential Function of the Form f(x) = b^x

Sketch a graph of [latex]f\left(x\right)={0.25}^{x}[/latex]. State the domain, range, and asymptote.

Answer: Before graphing, identify the behavior and create a table of points for the graph.

Since b = 0.25 is between zero and one, we know the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote y = 0.
Create a table of points.

x –3 –2 –1 0 1 2 3

[latex]f\left(x\right)={0.25}^{x}[/latex] 64 16 4 1 0.25 0.0625 0.015625
Plot the y-intercept, [latex]\left(0,1\right)[/latex], along with two other points. We can use [latex]\left(-1,4\right)[/latex] and [latex]\left(1,0.25\right)[/latex].

Draw a smooth curve connecting the points.

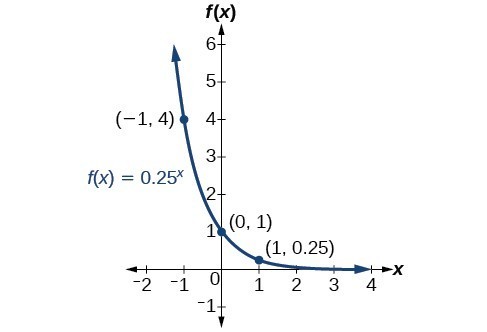Graph of the decaying exponential function f(x) = 0.25^x with labeled points at (-1, 4), (0, 1), and (1, 0.25).

The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(0,\infty \right)[/latex]; the horizontal asymptote is [latex]y=0[/latex].

Try It

Sketch the graph of [latex]f\left(x\right)={4}^{x}[/latex]. State the domain, range, and asymptote.

Answer: The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(0,\infty \right)[/latex]; the horizontal asymptote is [latex]y=0[/latex].

Licenses & Attributions

CC licensed content, Original

Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
Characteristics of Graphs of Exponential Functions Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/3pqyjsunkg. License: Public Domain: No Known Copyright.

CC licensed content, Shared previously

Question ID 3607. Provided by: Reidel,Jessica Authored by: Jay Abramson, et al.. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].

x	–3	–2	–1	0	1	2	3
[latex]f\left(x\right)={0.25}^{x}[/latex]	64	16	4	1	0.25	0.0625	0.015625

학습 가이드 > College Algebra