Operations on Polynomials
Learning Objectives
- Identify the degree, leading coefficient, and leading term of a polynomial
- Add and subtract polynomial expressions
- Multiply polynomials
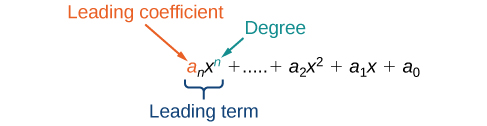
A General Note: Polynomials
A polynomial is an expression that can be written in the formHow To: Given a polynomial expression, identify the degree and leading coefficient.
- Find the highest power of x to determine the degree.
- Identify the term containing the highest power of x to find the leading term.
- Identify the coefficient of the leading term.
Example: Identifying the Degree and Leading Coefficient of a Polynomial
For the following polynomials, identify the degree, the leading term, and the leading coefficient.- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
- [latex]6p-{p}^{3}-2[/latex]
Answer:
- The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
- The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
- The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].
Try It
Identify the degree, leading term, and leading coefficient of the polynomial [latex]4{x}^{2}-{x}^{6}+2x - 6[/latex].Answer: The degree is 6, the leading term is [latex]-{x}^{6}[/latex], and the leading coefficient is [latex]-1[/latex].
Example: Subtracting Polynomials
Find the difference.[latex]\left(7{x}^{4}-{x}^{2}+6x+1\right)-\left(5{x}^{3}-2{x}^{2}+3x+2\right)[/latex]
Answer: [latex-display]\begin{array}{cc}7{x}^{4}-5{x}^{3}+\left(-{x}^{2}+2{x}^{2}\right)+\left(6x - 3x\right)+\left(1 - 2\right)\text{ }\hfill & \text{Combine like terms}.\hfill \\ 7{x}^{4}-5{x}^{3}+{x}^{2}+3x - 1\hfill & \text{Simplify}.\hfill \end{array}[/latex-display]
Analysis of the Solution
Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first.Try It
Find the difference. [latex-display]\left(-7{x}^{3}-7{x}^{2}+6x - 2\right)-\left(4{x}^{3}-6{x}^{2}-x+7\right)[/latex-display]Answer: [latex-display]-11{x}^{3}-{x}^{2}+7x - 9[/latex-display]
Using FOIL to Multiply Binomials
A shortcut called FOIL is sometimes used to find the product of two binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial. The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.
The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.
How To: Given two binomials, use FOIL to simplify the expression.
- Multiply the first terms of each binomial.
- Multiply the outer terms of the binomials.
- Multiply the inner terms of the binomials.
- Multiply the last terms of each binomial.
- Add the products.
- Combine like terms and simplify.
Example: Using FOIL to Multiply Binomials
Use FOIL to find the product.Answer:
Find the product of the first terms.
 Find the product of the outer terms.
Find the product of the outer terms.
 Find the product of the inner terms.
Find the product of the inner terms.
 Find the product of the last terms.
Find the product of the last terms.

[latex]\begin{array}{cc}6{x}^{2}+6x - 54x - 54\hfill & \text{Add the products}.\hfill \\ 6{x}^{2}+\left(6x - 54x\right)-54\hfill & \text{Combine like terms}.\hfill \\ 6{x}^{2}-48x - 54\hfill & \text{Simplify}.\hfill \end{array}[/latex]
Try It
Use FOIL to find the product. [latex-display]\left(x+7\right)\left(3x - 5\right)[/latex-display]Answer: [latex-display]3{x}^{2}+16x - 35[/latex-display]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Examples: Intro to Polynomials. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Examples: Adding and Subtracting Polynomials. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Exmaples: Multiplying Polynomials. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Question ID 93531, 93536, 93537, 93539. Authored by: Michael Jenck. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
- Question ID 3864. Authored by: Tyler Wallace. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
