We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Compound and Absolute Value Inequalities

Learning Objectives

  • Solve compound inequalities
  • Solve absolute value inequalities
A compound inequality includes two inequalities in one statement. A statement such as [latex]4<x\le 6[/latex] means [latex]4<x[/latex] and [latex]x\le 6[/latex]. There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Example: Solving a Compound Inequality

Solve the compound inequality: [latex]3\le 2x+2<6[/latex].

Answer: The first method is to write two separate inequalities: [latex]3\le 2x+2[/latex] and [latex]2x+2<6[/latex]. We solve them independently.

[latex]\begin{array}{lll}3\le 2x+2\hfill & \text{and}\hfill & 2x+2<6\hfill \\ 1\le 2x\hfill & \hfill & 2x<4\hfill \\ \frac{1}{2}\le x\hfill & \hfill & x<2\hfill \end{array}[/latex]
Then, we can rewrite the solution as a compound inequality, the same way the problem began.
[latex]\frac{1}{2}\le x<2[/latex]
In interval notation, the solution is written as [latex]\left[\frac{1}{2},2\right)[/latex]. The second method is to leave the compound inequality intact, and perform solving procedures on the three parts at the same time.
[latex]\begin{array}{ll}3\le 2x+2<6\hfill & \hfill \\ 1\le 2x<4\hfill & \text{Isolate the variable term, and subtract 2 from all three parts}.\hfill \\ \frac{1}{2}\le x<2\hfill & \text{Divide through all three parts by 2}.\hfill \end{array}[/latex]
We get the same solution: [latex]\left[\frac{1}{2},2\right)[/latex].

Try It

Solve the compound inequality [latex]4<2x - 8\le 10[/latex].

Answer: [latex]6<x\le 9\text{ }\text{ }\text{or}\left(6,9\right][/latex]

Solving Absolute Value Inequalities

As we know, the absolute value of a quantity is a positive number or zero. From the origin, a point located at [latex]\left(-x,0\right)[/latex] has an absolute value of [latex]x[/latex], as it is x units away. Consider absolute value as the distance from one point to another point. Regardless of direction, positive or negative, the distance between the two points is represented as a positive number or zero. An absolute value inequality is an equation of the form
[latex]|A|<B,|A|\le B,|A|>B,\text{or }|A|\ge B[/latex],
Where A, and sometimes B, represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all [latex]x[/latex] -values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values. There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph. Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of x-values such that the distance between [latex]x[/latex] and 600 is less than 200. We represent the distance between [latex]x[/latex] and 600 as [latex]|x - 600|[/latex], and therefore, [latex]|x - 600|\le 200[/latex] or
[latex]\begin{array}{c}-200\le x - 600\le 200\\ -200+600\le x - 600+600\le 200+600\\ 400\le x\le 800\end{array}[/latex]
This means our returns would be between $400 and $800. To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

A General Note: Absolute Value Inequalities

For an algebraic expression X, and [latex]k>0[/latex], an absolute value inequality is an inequality of the form
[latex]\begin{array}{l}|X|< k\text{ is equivalent to }-k< X< k\hfill \ |X|> k\text{ is equivalent to }X< -k\text{ or }X> k\hfill \end{array}[/latex]
These statements also apply to [latex]|X|\le k[/latex] and [latex]|X|\ge k[/latex].

Example: Determining a Number within a Prescribed Distance

Describe all values [latex]x[/latex] within a distance of 4 from the number 5.

Answer: We want the distance between [latex]x[/latex] and 5 to be less than or equal to 4. We can draw a number line to represent the condition to be satisfied. A number line with one tick mark in the center labeled: 5. The tick marks on either side of the center one are not marked. Arrows extend from the center tick mark to the outer tick marks, both are labeled 4. The distance from [latex]x[/latex] to 5 can be represented using an absolute value symbol, [latex]|x - 5|[/latex]. Write the values of [latex]x[/latex] that satisfy the condition as an absolute value inequality.

[latex]|x - 5|\le 4[/latex]
We need to write two inequalities as there are always two solutions to an absolute value equation.
[latex]\begin{array}{lll}x - 5\le 4\hfill & \text{and}\hfill & x - 5\ge -4\hfill \\ x\le 9\hfill & \hfill & x\ge 1\hfill \end{array}[/latex]
If the solution set is [latex]x\le 9[/latex] and [latex]x\ge 1[/latex], then the solution set is an interval including all real numbers between and including 1 and 9. So [latex]|x - 5|\le 4[/latex] is equivalent to [latex]\left[1,9\right][/latex] in interval notation.

Try It

Describe all x-values within a distance of 3 from the number 2.

Answer: [latex]|x - 2|\le 3[/latex]

Example: Solving an Absolute Value Inequality

Solve [latex]|x - 1|\le 3[/latex].

Answer:

[latex]\begin{array}{l}|x - 1|\le 3\hfill \\ \hfill \\ -3\le x - 1\le 3\hfill \\ \hfill \\ -2\le x\le 4\hfill \\ \hfill \\ \left[-2,4\right]\hfill \end{array}[/latex]

Example: Using a Graphical Approach to Solve Absolute Value Inequalities

Given the equation [latex]y=-\frac{1}{2}|4x - 5|+3[/latex], determine the x-values for which the y-values are negative.

Answer: We are trying to determine where [latex]y<0[/latex], which is when [latex]-\frac{1}{2}|4x - 5|+3<0[/latex]. We begin by isolating the absolute value.

[latex]\begin{array}{ll}-\frac{1}{2}|4x - 5|< -3\hfill & \text{Multiply both sides by -2, and reverse the inequality}.\hfill \\ |4x - 5|> 6\hfill & \hfill \end{array}[/latex]
Next, we solve for the equality [latex]|4x - 5|=6[/latex].
[latex]\begin{array}{lll}4x - 5=6\hfill & \hfill & 4x - 5=-6\hfill \\ 4x=11\hfill & \text{or}\hfill & 4x=-1\hfill \\ x=\frac{11}{4}\hfill & \hfill & x=-\frac{1}{4}\hfill \end{array}[/latex]
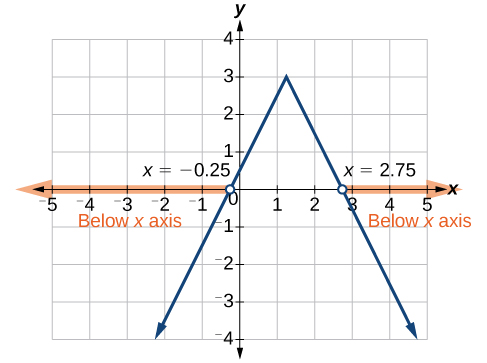
Now, we can examine the graph to observe where the y-values are negative. We observe where the branches are below the x-axis. Notice that it is not important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at [latex]x=-\frac{1}{4}[/latex] and [latex]x=\frac{11}{4}[/latex], and that the graph opens downward. A coordinate plan with the x-axis ranging from -5 to 5 and the y-axis ranging from -4 to 4. The function y = -1/2|4x – 5| + 3 is graphed. An open circle appears at the point -0.25 and an arrow

Try It

Solve [latex]-2|k - 4|\le -6[/latex].

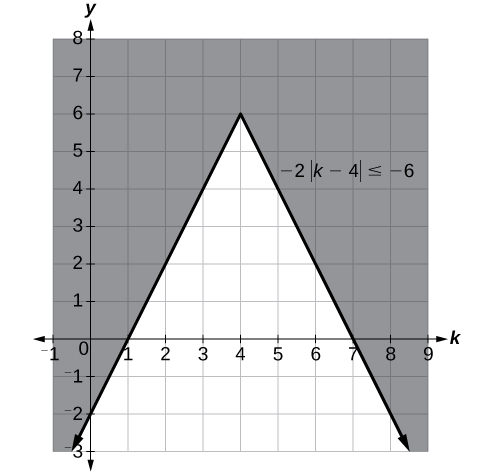
Answer: [latex]k\le 1[/latex] or [latex]k\ge 7[/latex]; in interval notation, this would be [latex]\left(-\infty ,1\right]\cup \left[7,\infty \right)[/latex]. A coordinate plane with the x-axis ranging from -1 to 9 and the y-axis ranging from -3 to 8. The function y = -2|k 4| + 6 is graphed and everything above the function is shaded in.

Try It

Sometimes a picture is worth a thousand words. You can turn a single variable inequality into a two variable inequality and make a graph. The x-intercepts of the graph will correspond with the solution to the inequality you can find by hand. Let's use the last example to try it, we will change the variable to x to make it easier to enter in Desmos. To turn [latex]-2|x - 4|\le -6[/latex] into a two variable equation, move everything to one side, and place the variable y on the other side, like this:

[latex]-2|x - 4|\le -6[/latex] [latex]-2|x - 4|+6\le y[/latex]

Now enter this inequality in Desmos and hover over the x-intercepts. If you need instruction on how to enter inequalities in Desmos, watch this tutorial.

https://youtu.be/2H3cAYmBdyI Are the x-values of the intercepts the same values as the solution we found above? [practice-area rows="2"][/practice-area]

Now you try turning this single variable inequality into a two variable inequality:

[latex]5|9-2x|\ge10[/latex]

Graph your inequality with Desmos, and write the solution interval. [practice-area rows="2"][/practice-area]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Learn Desmos: Inequalities. Authored by: Desmos. License: Public Domain: No Known Copyright.
  • Question ID 92608, 92609. Authored by: Michael Jenck. License: CC BY: Attribution. License terms: IMathAS Community License, CC-BY + GPL.
  • Question ID 89935. Authored by: Krystal Meier. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 15505. Authored by: Tophe Anderson. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.

CC licensed content, Specific attribution