Evaluate and Solve Functions
Learning Objectives
- Evaluate and solve functions in algebraic form
- Evaluate functions given tabular or graphical data
How To: Given the formula for a function, evaluate.
- Replace the input variable in the formula with the value provided.
- Calculate the result.
Example: Evaluating Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], evaluate [latex]h\left(4\right)[/latex].Answer:
To evaluate [latex]h\left(4\right)[/latex], we substitute the value 4 for the input variable [latex]p[/latex] in the given function. [latex]\begin{cases}\text{ }h\left(p\right)={p}^{2}+2p\hfill \\ \text{ }h\left(4\right)={\left(4\right)}^{2}+2\left(4\right)\hfill \\ \text{ }=16+8\hfill \\ \text{ }=24\hfill \end{cases}[/latex]
Therefore, for an input of 4, we have an output of 24.Example: Evaluating Functions at Specific Values
Evaluate [latex]f\left(x\right)={x}^{2}+3x - 4[/latex] at- [latex]2[/latex]
- [latex]a[/latex]
- [latex]a+h[/latex]
- [latex]\frac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]
Answer: Replace the [latex]x[/latex] in the function with each specified value.
- Because the input value is a number, 2, we can use algebra to simplify.
[latex]\begin{cases}f\left(2\right)={2}^{2}+3\left(2\right)-4\hfill \\ =4+6 - 4\hfill \\ =6\hfill \end{cases}[/latex]
- In this case, the input value is a letter so we cannot simplify the answer any further.
[latex]f\left(a\right)={a}^{2}+3a - 4[/latex]
- With an input value of [latex]a+h[/latex], we must use the distributive property.
[latex]\begin{cases}f\left(a+h\right)={\left(a+h\right)}^{2}+3\left(a+h\right)-4\hfill \\ ={a}^{2}+2ah+{h}^{2}+3a+3h - 4\hfill \end{cases}[/latex]
- In this case, we apply the input values to the function more than once, and then perform algebraic operations on the result. We already found that
[latex]f\left(a+h\right)={a}^{2}+2ah+{h}^{2}+3a+3h - 4[/latex]and we know that[latex]f\left(a\right)={a}^{2}+3a - 4[/latex]Now we combine the results and simplify.
[latex]\begin{cases}\begin{cases}\hfill \\ \frac{f\left(a+h\right)-f\left(a\right)}{h}=\frac{\left({a}^{2}+2ah+{h}^{2}+3a+3h - 4\right)-\left({a}^{2}+3a - 4\right)}{h}\hfill \end{cases}\hfill \\ \begin{cases}\text{ }=\frac{2ah+{h}^{2}+3h}{h}\hfill & \hfill \\ \text{ }=\frac{h\left(2a+h+3\right)}{h}\hfill & \begin{cases}{cc}\begin{cases}{cc}& \end{cases}& \end{cases}\text{Factor out }h.\hfill \\ \text{ }=2a+h+3\hfill & \begin{cases}{cc}\begin{cases}{cc}& \end{cases}& \end{cases}\text{Simplify}.\hfill \end{cases}\hfill \end{cases}[/latex]
Example: Solving Functions
Given the function [latex]h\left(p\right)={p}^{2}+2p[/latex], solve for [latex]h\left(p\right)=3[/latex].Answer:
[latex]\begin{cases}\text{ }h\left(p\right)=3\hfill & \hfill & \hfill & \hfill \\ \text{ }{p}^{2}+2p=3\hfill & \hfill & \hfill & \text{Substitute the original function }h\left(p\right)={p}^{2}+2p.\hfill \\ \text{ }{p}^{2}+2p - 3=0\hfill & \hfill & \hfill & \text{Subtract 3 from each side}.\hfill \\ \text{ }\left(p+3\text{)(}p - 1\right)=0\hfill & \hfill & \hfill & \text{Factor}.\hfill \end{cases}[/latex]
If [latex]\left(p+3\right)\left(p - 1\right)=0[/latex], either [latex]\left(p+3\right)=0[/latex] or [latex]\left(p - 1\right)=0[/latex] (or both of them equal 0). We will set each factor equal to 0 and solve for [latex]p[/latex] in each case.[latex]\begin{cases}\left(p+3\right)=0,\hfill & p=-3\hfill \\ \left(p - 1\right)=0,\hfill & p=1\hfill \end{cases}[/latex]
This gives us two solutions. The output [latex]h\left(p\right)=3[/latex] when the input is either [latex]p=1[/latex] or [latex]p=-3[/latex].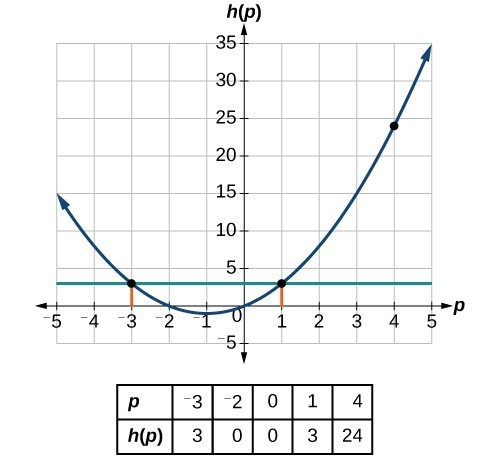 We can also verify by graphing as in Figure 5. The graph verifies that [latex]h\left(1\right)=h\left(-3\right)=3[/latex] and [latex]h\left(4\right)=24[/latex].
We can also verify by graphing as in Figure 5. The graph verifies that [latex]h\left(1\right)=h\left(-3\right)=3[/latex] and [latex]h\left(4\right)=24[/latex].
Try It
Given the function [latex]g\left(m\right)=\sqrt{m - 4}[/latex], solve [latex]g\left(m\right)=2[/latex].Answer: [latex-display]m=8[/latex-display]
Q & A
Are there relationships expressed by an equation that do represent a function but which still cannot be represented by an algebraic formula? Yes, this can happen. For example, given the equation [latex]x=y+{2}^{y}[/latex], if we want to express [latex]y[/latex] as a function of [latex]x[/latex], there is no simple algebraic formula involving only [latex]x[/latex] that equals [latex]y[/latex]. However, each [latex]x[/latex] does determine a unique value for [latex]y[/latex], and there are mathematical procedures by which [latex]y[/latex] can be found to any desired accuracy. In this case, we say that the equation gives an implicit (implied) rule for [latex]y[/latex] as a function of [latex]x[/latex], even though the formula cannot be written explicitly.Evaluating a Function Given in Tabular Form
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours. The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See the table below.| Pet | Memory span in hours |
|---|---|
| Puppy | 0.008 |
| Adult dog | 0.083 |
| Cat | 16 |
| Goldfish | 2160 |
| Beta fish | 3600 |
How To: Given a function represented by a table, identify specific output and input values.
- Find the given input in the row (or column) of input values.
- Identify the corresponding output value paired with that input value.
- Find the given output values in the row (or column) of output values, noting every time that output value appears.
- Identify the input value(s) corresponding to the given output value.
Example: Evaluating and Solving a Tabular Function
Using the table below,- Evaluate [latex]g\left(3\right)[/latex].
- Solve [latex]g\left(n\right)=6[/latex].
| n | 1 | 2 | 3 | 4 | 5 |
| g(n) | 8 | 6 | 7 | 6 | 8 |
Answer:
- Evaluating [latex]g\left(3\right)[/latex] means determining the output value of the function [latex]g[/latex] for the input value of [latex]n=3[/latex]. The table output value corresponding to [latex]n=3[/latex] is 7, so [latex]g\left(3\right)=7[/latex].
- Solving [latex]g\left(n\right)=6[/latex] means identifying the input values, [latex]n[/latex], that produce an output value of 6. The table below shows two solutions: [latex]n=2[/latex] and [latex]n=4[/latex].
| n | 1 | 2 | 3 | 4 | 5 |
| g(n) | 8 | 6 | 7 | 6 | 8 |
Try It
Using the table from the previous example, evaluate [latex]g\left(1\right)[/latex] .Answer: [latex]g\left(1\right)=8[/latex]
Try It
You can use Desmos to graph functions, find function values, and evaluate functions. Watch this short tutorial to learn how. https://youtu.be/jACDzJ-rmsM Now try the following with Desmos:- Graph the function [latex]f(x) = -\frac{1}{2}x^2+x+4[/latex] using function notation.
- Evaluate the function at x = 1
- Make a table of values that references the function. Include at least the interval [-5,5] for x-values.
- Solve the function for f(0)
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 111699. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Learn Desmos: Functions. License: All Rights Reserved. License terms: Standard YouTube License.
- Question ID 1647. Authored by: WebWork-Rochester, mb Lippman,David, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 97486. Authored by: Carmichael,Patrick. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 15766, 2886. Authored by: Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 3751. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
