We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Graph Linear Functions

Learning Objectives

  • Graph a linear function by plotting points
  • Graph a linear function using the slope and y-intercept
  • Graph a linear function using transformations
We previously saw that that the graph of a linear function is a straight line. We were also able to see the points of the function as well as the initial value from a graph. By graphing two functions, then, we can more easily compare their characteristics. There are three basic methods of graphing linear functions. The first is by plotting points and then drawing a line through the points. The second is by using the y-intercept and slope. And the third is by using transformations of the identity function [latex]f\left(x\right)=x[/latex].

Graphing a Function by Plotting Points

To find points of a function, we can choose input values, evaluate the function at these input values, and calculate output values. The input values and corresponding output values form coordinate pairs. We then plot the coordinate pairs on a grid. In general, we should evaluate the function at a minimum of two inputs in order to find at least two points on the graph. For example, given the function, [latex]f\left(x\right)=2x[/latex], we might use the input values 1 and 2. Evaluating the function for an input value of 1 yields an output value of 2, which is represented by the point (1, 2). Evaluating the function for an input value of 2 yields an output value of 4, which is represented by the point (2, 4). Choosing three points is often advisable because if all three points do not fall on the same line, we know we made an error.

How To: Given a linear function, graph by plotting points.

  1. Choose a minimum of two input values.
  2. Evaluate the function at each input value.
  3. Use the resulting output values to identify coordinate pairs.
  4. Plot the coordinate pairs on a grid.
  5. Draw a line through the points.

Example: Graphing by Plotting Points

Graph [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex] by plotting points.

Answer: Begin by choosing input values. This function includes a fraction with a denominator of 3, so let’s choose multiples of 3 as input values. We will choose 0, 3, and 6. Evaluate the function at each input value, and use the output value to identify coordinate pairs.

[latex]\begin{array}{l}x=0& & f\left(0\right)=-\frac{2}{3}\left(0\right)+5=5\Rightarrow \left(0,5\right)\\ x=3& & f\left(3\right)=-\frac{2}{3}\left(3\right)+5=3\Rightarrow \left(3,3\right)\\ x=6& & f\left(6\right)=-\frac{2}{3}\left(6\right)+5=1\Rightarrow \left(6,1\right)\end{array}[/latex]

Plot the coordinate pairs and draw a line through the points. The graph below is of the function [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex]. The graph of the linear function f\left(x\right)=-\frac{2}{3}x+5.

Analysis of the Solution

The graph of the function is a line as expected for a linear function. In addition, the graph has a downward slant, which indicates a negative slope. This is also expected from the negative constant rate of change in the equation for the function.

Try It

Graph [latex]f\left(x\right)=-\frac{3}{4}x+6[/latex] by plotting points.

Answer: cnx_precalc_figure_02_02_0022

Graphing a Linear Function Using Transformations

Another option for graphing is to use transformations of the identity function [latex]f\left(x\right)=x[/latex]. A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.

Vertical Stretch or Compression

In the equation [latex]f\left(x\right)=mx[/latex], the m is acting as the vertical stretch or compression of the identity function. When m is negative, there is also a vertical reflection of the graph. Notice that multiplying the equation of [latex]f\left(x\right)=x[/latex] by m stretches the graph of f by a factor of m units if m > 1 and compresses the graph of f by a factor of m units if 0 < m < 1. This means the larger the absolute value of m, the steeper the slope.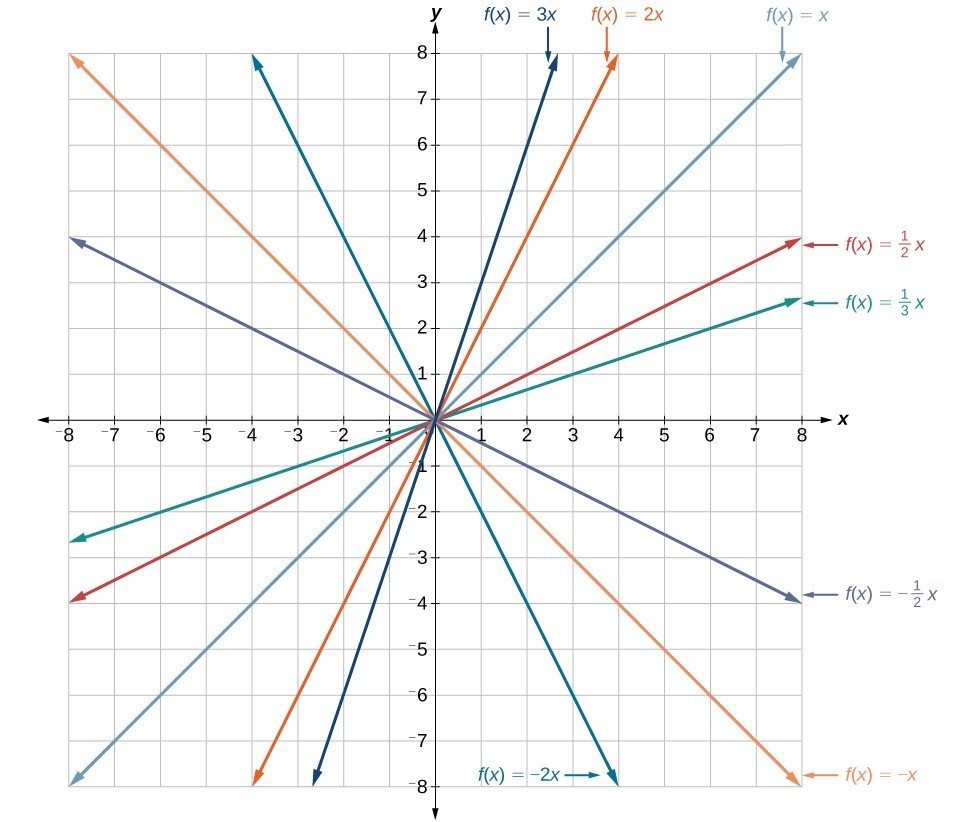
Graph with several linear functions including y = 3x, y = 2x, y = x, y = (1/2)x, y = (1/3)x, y = (-1/2)x, y = -x, and y = -2x Vertical stretches and compressions and reflections on the function [latex]f\left(x\right)=x[/latex].

Vertical Shift

In [latex]f\left(x\right)=mx+b[/latex], the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice that adding a value of b to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of f a total of b units up if b is positive and |b| units down if b is negative.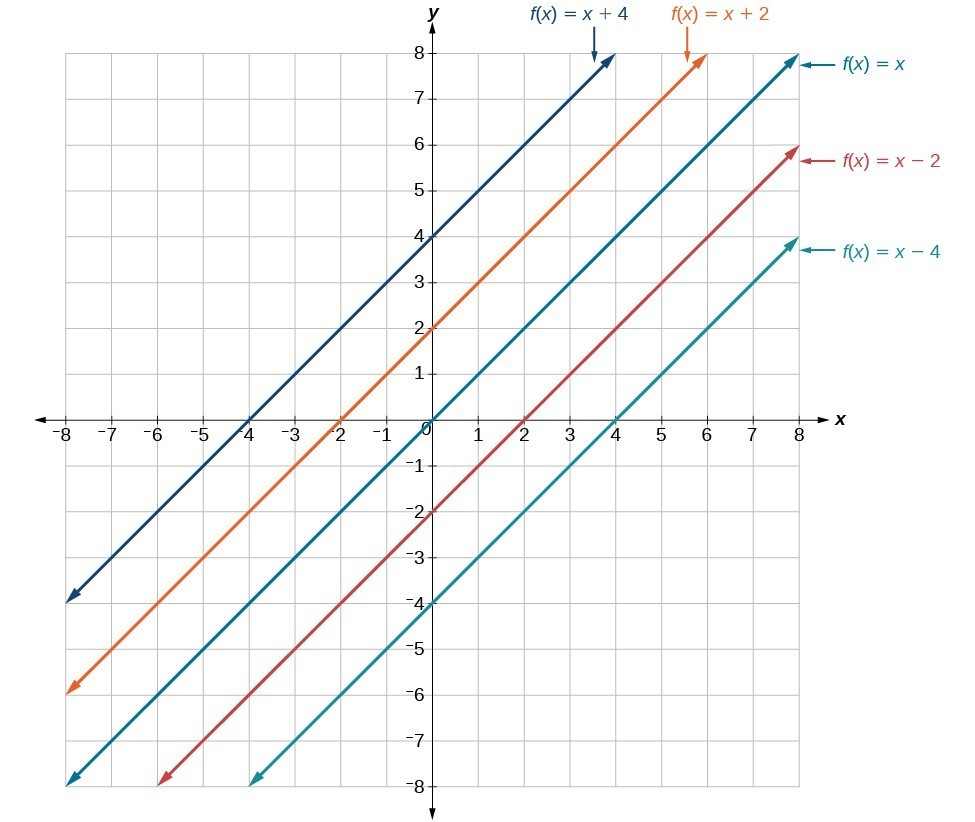
graph showing y = x , y = x+2, y = x+4, y = x-2, y = x-4 This graph illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].
Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.

How To: Given the equation of a linear function, use transformations to graph the linear function in the form [latex]f\left(x\right)=mx+b[/latex].

  1. Graph [latex]f\left(x\right)=x[/latex].
  2. Vertically stretch or compress the graph by a factor m.
  3. Shift the graph up or down b units.

Example: Graphing by Using Transformations

Graph [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex] using transformations.

Answer: The equation for the function shows that [latex]m=\frac{1}{2}[/latex] so the identity function is vertically compressed by [latex]\frac{1}{2}[/latex]. The equation for the function also shows that [latex]b=-3[/latex] so the identity function is vertically shifted down 3 units. First, graph the identity function, and show the vertical compression.

graph showing the lines y = x and y = (1/2)x The function, [latex]y=x[/latex], compressed by a factor of [latex]\frac{1}{2}[/latex].
Then show the vertical shift.
Graph showing the lines y = (1/2)x, and y = (1/2) + 3 The function [latex]y=\frac{1}{2}x[/latex], shifted down 3 units.

Try It

Graph [latex]f\left(x\right)=4+2x[/latex], using transformations.

Answer: cnx_precalc_figure_02_02_0092

Q & A

In Example: Graphing by Using Transformations, could we have sketched the graph by reversing the order of the transformations? No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first. For example, following the order: Let the input be 2.

[latex]\begin{array}{l}f\text{(2)}=\frac{\text{1}}{\text{2}}\text{(2)}-\text{3}\hfill \\ =\text{1}-\text{3}\hfill \\ =-\text{2}\hfill \end{array}[/latex]

Licenses & Attributions

CC licensed content, Original

  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Question ID 114584, 114587. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 69981. Authored by: Majerus,Ryan. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 88183. Authored by: Shahbazian,Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.