We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Graphs of Ellipses

Learning Objectives

  • Sketch a graph of an ellipse centered at the origin
  • Sketch a graph of an ellipse not centered at the origin
  • Express the equation of an ellipse in standard form given the equation in general form
Just as we can write the equation for an ellipse given its graph, we can graph an ellipse given its equation. To graph ellipses centered at the origin, we use the standard form [latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1,\text{ }a>b[/latex] for horizontal ellipses and [latex]\frac{{x}^{2}}{{b}^{2}}+\frac{{y}^{2}}{{a}^{2}}=1,\text{ }a>b[/latex] for vertical ellipses.

How To: Given the standard form of an equation for an ellipse centered at [latex]\left(0,0\right)[/latex], sketch the graph.

  • Use the standard forms of the equations of an ellipse to determine the major axis, vertices, co-vertices, and foci.
    • If the equation is in the form [latex]\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex], then
      • the major axis is the x-axis
      • the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
      • the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
      • the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex]
    • If the equation is in the form [latex]\frac{{x}^{2}}{{b}^{2}}+\frac{{y}^{2}}{{a}^{2}}=1[/latex], where [latex]a>b[/latex], then
      • the major axis is the y-axis
      • the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
      • the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
      • the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex]
  • Solve for [latex]c[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
  • Plot the center, vertices, co-vertices, and foci in the coordinate plane, and draw a smooth curve to form the ellipse.

Example: Graphing an Ellipse Centered at the Origin

Graph the ellipse given by the equation, [latex]\frac{{x}^{2}}{9}+\frac{{y}^{2}}{25}=1[/latex]. Identify and label the center, vertices, co-vertices, and foci.

Answer: First, we determine the position of the major axis. Because [latex]25>9[/latex], the major axis is on the y-axis. Therefore, the equation is in the form [latex]\frac{{x}^{2}}{{b}^{2}}+\frac{{y}^{2}}{{a}^{2}}=1[/latex], where [latex]{b}^{2}=9[/latex] and [latex]{a}^{2}=25[/latex]. It follows that:

  • the center of the ellipse is [latex]\left(0,0\right)[/latex]
  • the coordinates of the vertices are [latex]\left(0,\pm a\right)=\left(0,\pm \sqrt{25}\right)=\left(0,\pm 5\right)[/latex]
  • the coordinates of the co-vertices are [latex]\left(\pm b,0\right)=\left(\pm \sqrt{9},0\right)=\left(\pm 3,0\right)[/latex]
  • the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex] Solving for [latex]c[/latex], we have:

[latex]\begin{array}{l}c=\pm \sqrt{{a}^{2}-{b}^{2}}\hfill \\ =\pm \sqrt{25 - 9}\hfill \\ =\pm \sqrt{16}\hfill \\ =\pm 4\hfill \end{array}[/latex]

Therefore, the coordinates of the foci are [latex]\left(0,\pm 4\right)[/latex]. Next, we plot and label the center, vertices, co-vertices, and foci, and draw a smooth curve to form the ellipse.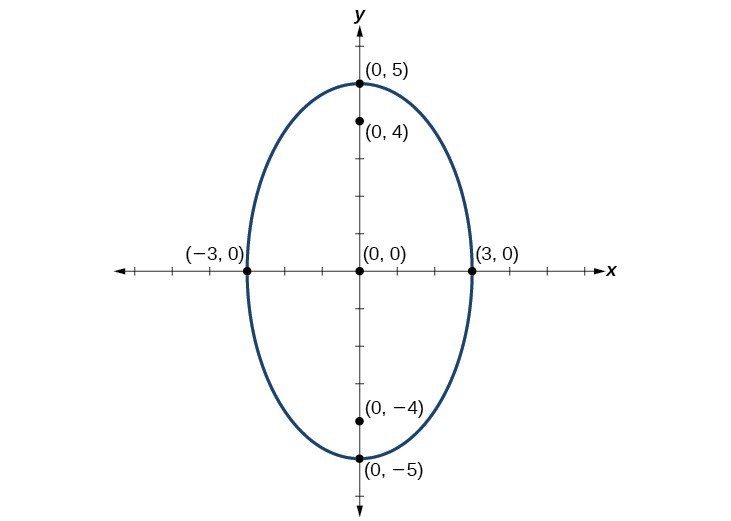

Try It

Graph the ellipse given by the equation [latex]\frac{{x}^{2}}{36}+\frac{{y}^{2}}{4}=1[/latex]. Identify and label the center, vertices, co-vertices, and foci.

Answer: center: [latex]\left(0,0\right)[/latex]; vertices: [latex]\left(\pm 6,0\right)[/latex]; co-vertices: [latex]\left(0,\pm 2\right)[/latex]; foci: [latex]\left(\pm 4\sqrt{2},0\right)[/latex]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 23514. Authored by: Shahbazian,Roy, mb McClure,Caren, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Specific attribution