We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Horizontal Asymptotes and Intercepts

Learning Objectives

  • Use the degree of the numerator and denominator of a rational function to determine what kind of horizontal asymptote it will have
  • Claculate slanted asymptotes
  • Determine the intercepts of a rational function in factored form
While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions. There are three distinct outcomes when checking for horizontal asymptotes: Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y = 0.

[latex]\text{Example: }f\left(x\right)=\frac{4x+2}{{x}^{2}+4x - 5}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx \frac{4x}{{x}^{2}}=\frac{4}{x}[/latex]. This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=\frac{4}{x}[/latex], and the outputs will approach zero, resulting in a horizontal asymptote at y = 0. Note that this graph crosses the horizontal asymptote.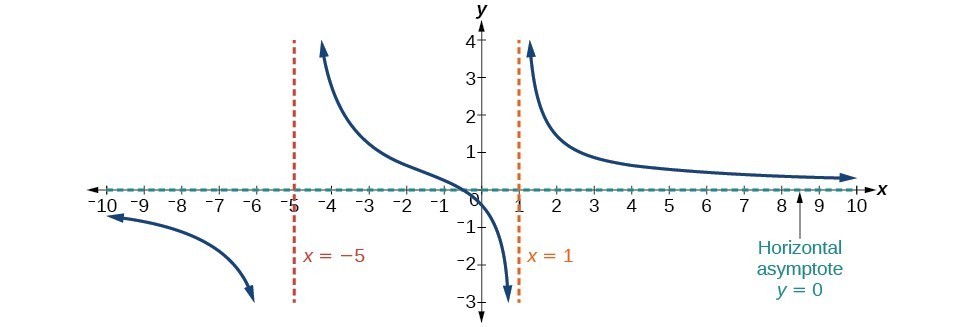
Graph of f(x)=(4x+2)/(x^2+4x-5) with its vertical asymptotes at x=-5 and x=1 and its horizontal asymptote at y=0. Horizontal Asymptote y = 0 when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne{0}\text{ where degree of }p<\text{degree of q}[/latex].
Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.

[latex]\text{Example: }f\left(x\right)=\frac{3{x}^{2}-2x+1}{x - 1}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{x}=3x[/latex]. This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=3x[/latex]. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of [latex]g\left(x\right)=3x[/latex] looks like a diagonal line, and since f will behave similarly to g, it will approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote.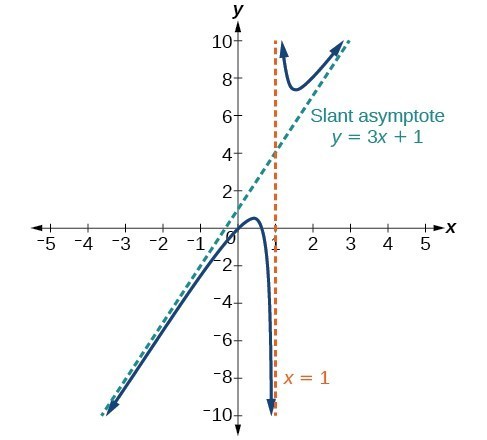
Graph of f(x)=(3x^2-2x+1)/(x-1) with its vertical asymptote at x=1 and a slant asymptote aty=3x+1. Slant Asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex] where degree of [latex]p>\text{ degree of }q\text{ by }1[/latex].
To find the equation of the slant asymptote, divide [latex]\frac{3{x}^{2}-2x+1}{x - 1}[/latex]. The quotient is [latex]3x+1[/latex], and the remainder is 2. The slant asymptote is the graph of the line [latex]g\left(x\right)=3x+1[/latex]. Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at [latex]y=\frac{{a}_{n}}{{b}_{n}}[/latex], where [latex]{a}_{n}[/latex] and [latex]{b}_{n}[/latex] are the leading coefficients of [latex]p\left(x\right)[/latex] and [latex]q\left(x\right)[/latex] for [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex]. [latex-display]\text{Example: }f\left(x\right)=\frac{3{x}^{2}+2}{{x}^{2}+4x - 5}[/latex-display] In this case, the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{{x}^{2}}=3[/latex]. This tells us that as the inputs grow large, this function will behave like the function [latex]g\left(x\right)=3[/latex], which is a horizontal line. As [latex]x\to \pm \infty ,f\left(x\right)\to 3[/latex], resulting in a horizontal asymptote at y = 3. Note that this graph crosses the horizontal asymptote.
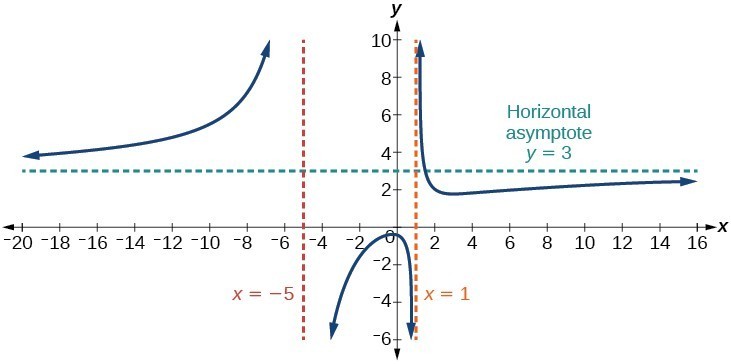Graph of f(x)=(3x^2+2)/(x^2+4x-5) with its vertical asymptotes at x=-5 and x=1 and its horizontal asymptote at y=3. Horizontal Asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{where degree of }p=\text{degree of }q[/latex].
Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote. It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

[latex]f\left(x\right)=\frac{3{x}^{5}-{x}^{2}}{x+3}[/latex]

with end behavior

[latex]f\left(x\right)\approx \frac{3{x}^{5}}{x}=3{x}^{4}[/latex],

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

[latex]x\to \pm \infty , f\left(x\right)\to \infty [/latex]

Try it

A rational function [latex]f(x)[/latex] is graphed below.  Use the sliders to obtain graphs with the following horizontal asymptotes:
  1. Find values of a and b that will give a graph with a slant asymptote.
  2. Find values of a and b that will give a graph with a horizontal asymptote at [latex]y = o[/latex]
  3. Find values of a and b that will give a graph with a horizontal asymptote that is the ratio of the leading coefficients of [latex]f(x)[/latex].
https://www.desmos.com/calculator/d8eejzinsf

Answer: Answers will vary.

  1. Find values of a and b that will give a graph with a slant asymptote.  For example [latex]b = 3, a = 4[/latex]
  2. Find values of a and b that will give a graph with a horizontal asymptote at [latex]y = o[/latex].  For example, [latex]b = 4, a = 2[/latex]
  3. Find values of a and b that will give a graph with a horizontal asymptote that is the ratio of the leading coefficients of [latex]f(x)[/latex].For example, [latex]b = 4, a = 4[/latex]

 

A General Note: Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
  • Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.
  • Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
  • Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Example: Identifying Horizontal and Slant Asymptotes

For the functions below, identify the horizontal or slant asymptote.
  1. [latex]g\left(x\right)=\frac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}[/latex]
  2. [latex]h\left(x\right)=\frac{{x}^{2}-4x+1}{x+2}[/latex]
  3. [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{3}-8}[/latex]

Answer: For these solutions, we will use [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}, q\left(x\right)\ne 0[/latex].

  1. [latex]g\left(x\right)=\frac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}[/latex]: The degree of [latex]p=\text{degree of} q=3[/latex], so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at [latex]y=\frac{6}{2}[/latex] or [latex]y=3[/latex].
  2. [latex]h\left(x\right)=\frac{{x}^{2}-4x+1}{x+2}[/latex]: The degree of [latex]p=2[/latex] and degree of [latex]q=1[/latex]. Since [latex]p>q[/latex] by 1, there is a slant asymptote found at [latex]\frac{{x}^{2}-4x+1}{x+2}[/latex].
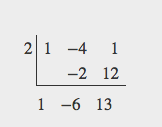Screen Shot 2015-11-10 at 4.25.52 PM The quotient is [latex]x - 2[/latex] and the remainder is 13. There is a slant asymptote at [latex]y=-x - 2[/latex]. [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{3}-8}[/latex]: The degree of [latex]p=2\text{ }<[/latex] degree of [latex]q=3[/latex], so there is a horizontal asymptote y = 0.

Watch this video to see more worked examples of determining which kind of horizontal asymptote a rational function will have. https://youtu.be/A1tApZSE8nI

Example: Identifying Horizontal Asymptotes

In the sugar concentration problem earlier, we created the equation [latex]C\left(t\right)=\frac{5+t}{100+10t}[/latex]. Find the horizontal asymptote and interpret it in context of the problem.

Answer: Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is t, with coefficient 1. In the denominator, the leading term is 10t, with coefficient 10. The horizontal asymptote will be at the ratio of these values:

[latex]t\to \infty , C\left(t\right)\to \frac{1}{10}[/latex]

This function will have a horizontal asymptote at [latex]y=\frac{1}{10}[/latex]. This tells us that as the values of t increase, the values of C will approach [latex]\frac{1}{10}[/latex]. In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or [latex]\frac{1}{10}[/latex] pounds per gallon.

Example: Identifying Horizontal and Vertical Asymptotes

Find the horizontal and vertical asymptotes of the function

[latex]f\left(x\right)=\frac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex]

Answer: First, note that this function has no common factors, so there are no potential removable discontinuities. The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at [latex]x=1,-2,\text{and }5[/latex], indicating vertical asymptotes at these values. The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as [latex]x\to \pm \infty , f\left(x\right)\to 0[/latex]. This function will have a horizontal asymptote at [latex]y=0[/latex]. Graph of f(x)=(x-2)(x+3)/(x-1)(x+2)(x-5) with its vertical asymptotes at x=-2, x=1, and x=5 and its horizontal asymptote at y=0.

Try It

Find the vertical and horizontal asymptotes of the function:

[latex]f\left(x\right)=\frac{\left(2x - 1\right)\left(2x+1\right)}{\left(x - 2\right)\left(x+3\right)}[/latex]

Answer: Vertical asymptotes at [latex]x=2[/latex] and [latex]x=-3[/latex]; horizontal asymptote at [latex]y=4[/latex].

A General Note: Intercepts of Rational Functions

A rational function will have a y-intercept when the input is zero, if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero. Likewise, a rational function will have x-intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x-intercepts can only occur when the numerator of the rational function is equal to zero.

Example: Finding the Intercepts of a Rational Function

Find the intercepts of [latex]f\left(x\right)=\frac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex].

Answer: We can find the y-intercept by evaluating the function at zero

[latex]\begin{array}{l}f\left(0\right)=\frac{\left(0 - 2\right)\left(0+3\right)}{\left(0 - 1\right)\left(0+2\right)\left(0 - 5\right)}\hfill \\ \text{ }=\frac{-6}{10}\hfill \\ \text{ }=-\frac{3}{5}\hfill \\ \text{ }=-0.6\hfill \end{array}[/latex]

The x-intercepts will occur when the function is equal to zero:

[latex]\begin{array}{l} 0=\frac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}\hfill & \text{This is zero when the numerator is zero}.\hfill \\ 0=\left(x - 2\right)\left(x+3\right)\hfill & \hfill \\ x=2, -3\hfill & \hfill \end{array}[/latex]

The y-intercept is [latex]\left(0,-0.6\right)[/latex], the x-intercepts are [latex]\left(2,0\right)[/latex] and [latex]\left(-3,0\right)[/latex].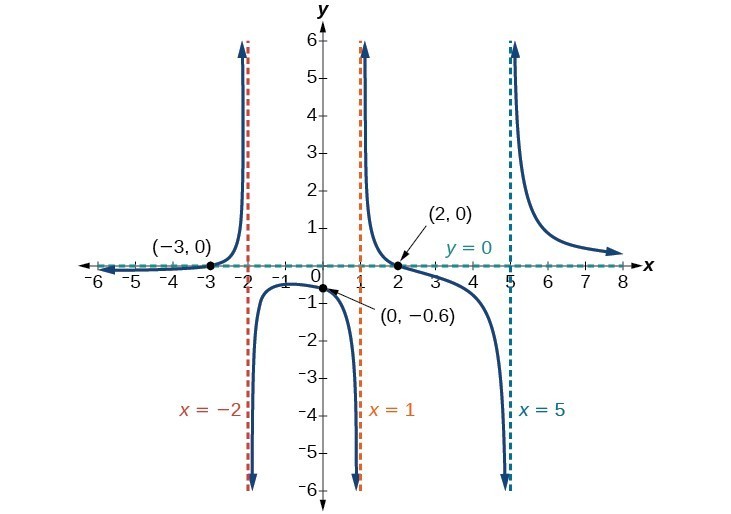 Graph of f(x)=(x-2)(x+3)/(x-1)(x+2)(x-5) with its vertical asymptotes at x=-2, x=1, and x=5, its horizontal asymptote at y=0, and its intercepts at (-3, 0), (0, -0.6), and (2, 0).

Try It

Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x- and y-intercepts and the horizontal and vertical asymptotes.

Answer: For the transformed reciprocal squared function, we find the rational form. [latex]f\left(x\right)=\frac{1}{{\left(x - 3\right)}^{2}}-4=\frac{1 - 4{\left(x - 3\right)}^{2}}{{\left(x - 3\right)}^{2}}=\frac{1 - 4\left({x}^{2}-6x+9\right)}{\left(x - 3\right)\left(x - 3\right)}=\frac{-4{x}^{2}+24x - 35}{{x}^{2}-6x+9}[/latex] Because the numerator is the same degree as the denominator we know that as [latex]x\to \pm \infty , f\left(x\right)\to -4; \text{so } y=-4[/latex] is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is [latex]x=3[/latex], because as [latex]x\to 3,f\left(x\right)\to \infty[/latex]. We then set the numerator equal to 0 and find the x-intercepts are at [latex]\left(2.5,0\right)[/latex] and [latex]\left(3.5,0\right)[/latex]. Finally, we evaluate the function at 0 and find the y-intercept to be at [latex]\left(0,\frac{-35}{9}\right)[/latex].

Watch the following video to see more worked examples of finding asymptotes, intercepts and holes of rational functions. https://youtu.be/UnVZs2EaEjI

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Question ID 129072. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
  • Question ID 105058. Authored by: Smart, Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 15836. Authored by: James Sousa . License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Ex: Determine Horizontal Asymptotes of Rational Functions . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Find the Intercepts, Asymptotes, and Hole of a Rational Function . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.