Intercepts of Quadratic Functions
Learning Objectives
- Find the y-intercept of a quadratic function
- Find the real-number x-intercepts, or roots of a quadratic function using factoring and the quadratic formula
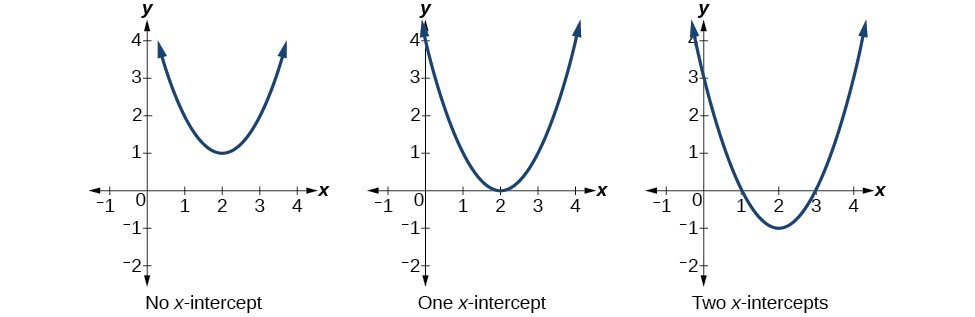 Number of x-intercepts of a parabola
Number of x-intercepts of a parabolaHow To: Given a quadratic function [latex]f\left(x\right)[/latex], find the y- and x-intercepts.
- Evaluate [latex]f\left(0\right)[/latex] to find the y-intercept.
- Solve the quadratic equation [latex]f\left(x\right)=0[/latex] to find the x-intercepts.
Example: Finding the y- and x-Intercepts of a Parabola
Find the y- and x-intercepts of the quadratic [latex]f\left(x\right)=3{x}^{2}+5x - 2[/latex].Answer: We find the y-intercept by evaluating [latex]f\left(0\right)[/latex].
[latex]\begin{array}{c}f\left(0\right)=3{\left(0\right)}^{2}+5\left(0\right)-2\hfill \\ \text{ }=-2\hfill \end{array}[/latex]
So the y-intercept is at [latex]\left(0,-2\right)[/latex]. For the x-intercepts, or roots, we find all solutions of [latex]f\left(x\right)=0[/latex].[latex]0=3{x}^{2}+5x - 2[/latex]
In this case, the quadratic can be factored easily, providing the simplest method for solution.[latex]0=\left(3x - 1\right)\left(x+2\right)[/latex] [latex]\begin{array}{c}0=3x - 1\hfill & \hfill & \hfill & \hfill & 0=x+2\hfill \\ x=\frac{1}{3}\hfill & \hfill & \text{or}\hfill & \hfill & x=-2\hfill \end{array}[/latex]
So the roots are at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].Analysis of the Solution
By graphing the function, we can confirm that the graph crosses the y-axis at [latex]\left(0,-2\right)[/latex]. We can also confirm that the graph crosses the x-axis at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].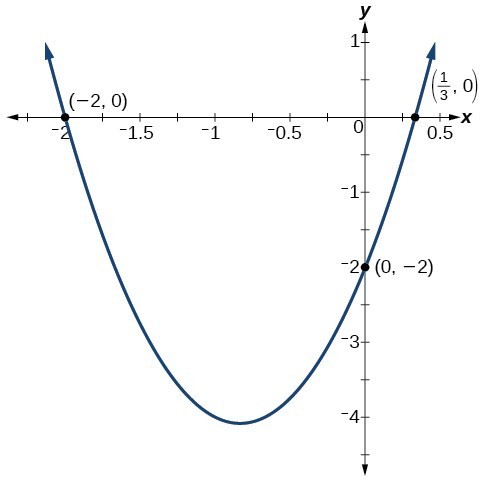
How To: Given a quadratic function, find the x-intercepts by rewriting in standard form.
- Substitute a and b into [latex]h=-\frac{b}{2a}[/latex].
- Substitute x = h into the general form of the quadratic function to find k.
- Rewrite the quadratic in standard form using h and k.
- Solve for when the output of the function will be zero to find the x-intercepts.
Example: Finding the Roots of a Parabola
Find the x-intercepts of the quadratic function [latex]f\left(x\right)=2{x}^{2}+4x - 4[/latex].Answer: We begin by solving for when the output will be zero.
[latex]0=2{x}^{2}+4x - 4[/latex]
Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]
We know that a = 2. Then we solve for h and k.[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill & \hfill & \hfill & k=f\left(-1\right)\hfill \\ \text{ }=-\frac{4}{2\left(2\right)}\hfill & \hfill & \hfill & \text{ }=2{\left(-1\right)}^{2}+4\left(-1\right)-4\hfill \\ \text{ }=-1\hfill & \hfill & \hfill & \text{ }=-6\hfill \end{array}[/latex]
So now we can rewrite in standard form.[latex]f\left(x\right)=2{\left(x+1\right)}^{2}-6[/latex]
We can now solve for when the output will be zero.[latex]\begin{array}{c}0=2{\left(x+1\right)}^{2}-6\hfill \\ 6=2{\left(x+1\right)}^{2}\hfill \\ 3={\left(x+1\right)}^{2}\hfill \\ x+1=\pm \sqrt{3}\hfill \\ x=-1\pm \sqrt{3}\hfill \end{array}[/latex]
The graph has x-intercepts at [latex]\left(-1-\sqrt{3},0\right)[/latex] and [latex]\left(-1+\sqrt{3},0\right)[/latex].Analysis of the Solution
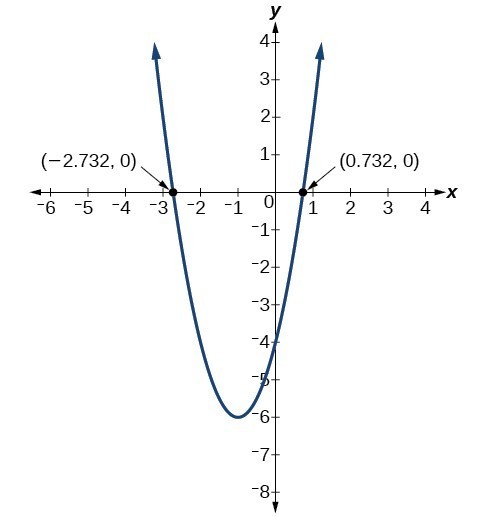 We can check our work by graphing the given function on a graphing utility and observing the roots.
We can check our work by graphing the given function on a graphing utility and observing the roots.
Try It
The function [latex]g\left(x\right)=13+{x}^{2}-6x[/latex] is graphed below. You can use Desmos to find the x-and y-intercepts by clicking on the graph. Four points will appear. List each point, and what kind of point it is, we got you started with the vertex:- Vertex = [latex](3,-16)[/latex]
Answer: y-intercept at (0, 13)
Licenses & Attributions
CC licensed content, Original
- Question ID 121416. Provided by: Lumen Learning License: CC BY: Attribution. License terms: MathAS Community License CC-BY + GPL.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Question ID 15809. Authored by: Sousa,James, mb Lippman,David. License: CC BY: Attribution. License terms: MathAS Community License CC-BY + GPL.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
