Local Behavior of Polynomial Functions
Learning Objectives
- Identify turning points of polynomial functions from a graph
- Identify the number of turning points and intercepts of a polynomial from it's degree
- Determine x and y-intercepts of a polynomial function given it's equation in factored form
Identifying Local Behavior of Polynomial Functions
In addition to the end behavior of polynomial functions, we are also interested in what happens in the "middle" of the function. In particular, we are interested in locations where graph behavior changes. A turning point is a point at which the function values change from increasing to decreasing or decreasing to increasing.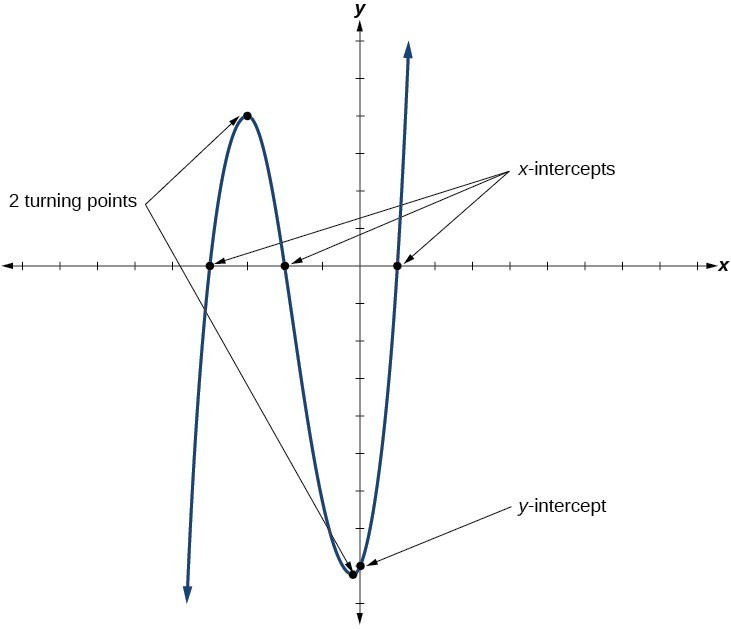
We are also interested in the intercepts. As with all functions, the y-intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Because a polynomial is a function, only one output value corresponds to each input value so there can be only one y-intercept [latex]\left(0,{a}_{0}\right)[/latex]. The x-intercepts occur at the input values that correspond to an output value of zero. It is possible to have more than one x-intercept.
A General Note: Intercepts and Turning Points of Polynomial Functions
- A turning point of a graph is a point at which the graph changes direction from increasing to decreasing or decreasing to increasing.
- The y-intercept is the point at which the function has an input value of zero.
- The x-intercepts are the points at which the output value is zero.
- A polynomial of degree n will have, at most, n x-intercepts and n – 1 turning points.
Determining the Number of Turning Points and Intercepts from the Degree of the Polynomial
A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must always occur at rounded curves. The graphs of polynomial functions are both continuous and smooth. The degree of a polynomial function helps us to determine the number of x-intercepts and the number of turning points. A polynomial function of nth degree is the product of n factors, so it will have at most n roots or zeros, or x-intercepts. The graph of the polynomial function of degree n must have at most n – 1 turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than the number of factors.Example: Determining the Number of Intercepts and Turning Points of a Polynomial
Without graphing the function, determine the local behavior of the function by finding the maximum number of x-intercepts and turning points for [latex]f\left(x\right)=-3{x}^{10}+4{x}^{7}-{x}^{4}+2{x}^{3}[/latex].Answer: The polynomial has a degree of 10, so there are at most 10 x-intercepts and at most [latex]10 – 1 = 9[/latex] turning points.
Try It
Without graphing the function, determine the maximum number of x-intercepts and turning points for [latex]f\left(x\right)=108 - 13{x}^{9}-8{x}^{4}+14{x}^{12}+2{x}^{3}[/latex]Answer: There are at most 12 x-intercepts and at most 11 turning points.
Example: Drawing Conclusions about a Polynomial Function from the Factors
Given the function [latex]f\left(x\right)=-4x\left(x+3\right)\left(x - 4\right)[/latex], determine the local behavior.Answer: The y-intercept is found by evaluating [latex]f\left(0\right)[/latex].
[latex]\begin{array}{c}f\left(0\right)=-4\left(0\right)\left(0+3\right)\left(0 - 4\right)\hfill \hfill \\ \text{ }=0\hfill \end{array}[/latex]
The y-intercept is [latex]\left(0,0\right)[/latex]. The x-intercepts are found by determining the zeros of the function.[latex]\begin{array}{c}0=-4x\left(x+3\right)\left(x - 4\right)\\ x=0\hfill & \hfill & \text{or}\hfill & \hfill & x+3=0\hfill & \hfill & \text{or}\hfill & \hfill & x - 4=0\hfill \\ x=0\hfill & \hfill & \text{or}\hfill & \hfill & \text{ }x=-3\hfill & \hfill & \text{or}\hfill & \hfill & \text{ }x=4\end{array}[/latex]
The x-intercepts are [latex]\left(0,0\right),\left(-3,0\right)[/latex], and [latex]\left(4,0\right)[/latex]. The degree is 3 so the graph has at most 2 turning points.Try It
Given the function [latex]f\left(x\right)=0.2\left(x - 2\right)\left(x+1\right)\left(x - 5\right)[/latex], determine the local behavior.
Answer: The x-intercepts are [latex]\left(2,0\right),\left(-1,0\right)[/latex], and [latex]\left(5,0\right)[/latex], the y-intercept is [latex]\left(0,\text{2}\right)[/latex], and the graph has at most 2 turning points.
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 123739. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Question ID 15937. Authored by: Sousa, James. License: Other. License terms: iMathAS/ WAMAP/ MyOpenMath Community License (GPL + CC-BY).
- Turning Points and X-Intercepts of a Polynomial Function. Authored by: Sousa, James (Mathispower4u). License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
