Writing Equations of Lines
Learning Objectives
- Use the slope intercept form to plot and write equations of lines
- Use the point-slope formula to write the equation of a line
- Write the equation of a line in standard form
- Recognize vertical and horizontal lines from their graphs and equations
Slope-Intercept Form
Perhaps the most familiar form of a linear equation is the slope-intercept form, written as [latex]y=mx+b[/latex], where [latex]m=\text{slope}[/latex] and [latex]b=y\text{-intercept}[/latex]. Let us begin with the slope.The Slope of a Line
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown below. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].
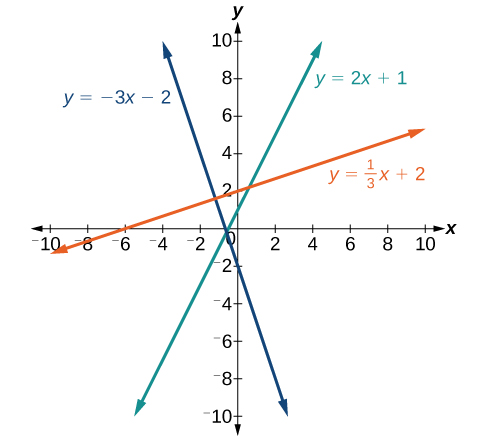
A General Note: The Slope of a Line
The slope of a line, m, represents the change in y over the change in x. Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:[latex]m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
Example: Finding the Slope of a Line Given Two Points
Find the slope of a line that passes through the points [latex]\left(2,-1\right)[/latex] and [latex]\left(-5,3\right)[/latex].Answer: We substitute the y-values and the x-values into the formula.
[latex]\begin{array}{l}m\hfill&=\frac{3-\left(-1\right)}{-5 - 2}\hfill \\ \hfill&=\frac{4}{-7}\hfill \\ \hfill&=-\frac{4}{7}\hfill \end{array}[/latex]
The slope is [latex]-\frac{4}{7}[/latex].
Analysis of the Solution
It does not matter which point is called [latex]\left({x}_{1},{y}_{1}\right)[/latex] or [latex]\left({x}_{2},{y}_{2}\right)[/latex]. As long as we are consistent with the order of the y terms and the order of the x terms in the numerator and denominator, the calculation will yield the same result.Try It
Find the slope of the line that passes through the points [latex]\left(-2,6\right)[/latex] and [latex]\left(1,4\right)[/latex].Answer: [latex]x=-5[/latex]
Example: Finding the Equation of a Line Passing Through Two Given Points
Find the equation of the line passing through the points [latex]\left(3,4\right)[/latex] and [latex]\left(0,-3\right)[/latex]. Write the final equation in slope-intercept form.Answer: First, we calculate the slope using the slope formula and two points.
[latex]\begin{array}{l}\hfill \\ m=\frac{-3 - 4}{0 - 3}\hfill \\ =\frac{-7}{-3}\hfill \\ =\frac{7}{3}\hfill \end{array}[/latex]
Next, we use the point-slope formula with the slope of [latex]\frac{7}{3}[/latex], and either point. Let’s pick the point [latex]\left(3,4\right)[/latex] for [latex]\left({x}_{1},{y}_{1}\right)[/latex].
[latex]\begin{array}{l}y - 4=\frac{7}{3}\left(x - 3\right)\hfill \\ y - 4=\frac{7}{3}x - 7\hfill&\text{Distribute the }\frac{7}{3}.\hfill \\ y=\frac{7}{3}x - 3\hfill \end{array}[/latex]
In slope-intercept form, the equation is written as [latex]y=\frac{7}{3}x - 3[/latex].
Analysis of the Solution
To prove that either point can be used, let us use the second point [latex]\left(0,-3\right)[/latex] and see if we get the same equation.
[latex]\begin{array}{l}y-\left(-3\right)=\frac{7}{3}\left(x - 0\right)\hfill \\ y+3=\frac{7}{3}x\hfill \\ y=\frac{7}{3}x - 3\hfill \end{array}[/latex]
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Standard Form of a Line
Another way that we can represent the equation of a line is in standard form. Standard form is given as[latex]Ax+By=C[/latex]
where [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] are integers. The x- and y-terms are on one side of the equal sign and the constant term is on the other side.
Example: Finding the Equation of a Line and Writing It in Standard Form
Find the equation of the line with [latex]m=-6[/latex] and passing through the point [latex]\left(\frac{1}{4},-2\right)[/latex]. Write the equation in standard form.Answer: We begin using the point-slope formula.
[latex]\begin{array}{l}y-\left(-2\right)=-6\left(x-\frac{1}{4}\right)\hfill \\ y+2=-6x+\frac{3}{2}\hfill \end{array}[/latex]
From here, we multiply through by 2, as no fractions are permitted in standard form, and then move both variables to the left aside of the equal sign and move the constants to the right.
[latex]\begin{array}{l}2\left(y+2\right)=\left(-6x+\frac{3}{2}\right)2\hfill \\ 2y+4=-12x+3\hfill \\ 12x+2y=-1\hfill \end{array}[/latex]
This equation is now written in standard form.
Try It
Find the equation of the line in standard form with slope [latex]m=-\frac{1}{3}[/latex] and passing through the point [latex]\left(1,\frac{1}{3}\right)[/latex].Answer: [latex]x+3y=2[/latex]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 1719. Authored by: Barbara Goldner. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
- Question ID 110942, 110946, 110951, 110952. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC- BY + GPL.
CC licensed content, Specific attribution
- College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
