Methods for Solving a System of Nonlinear Equations
Learning Objectives
- Solve a system that represents the intersection of a parabola and a line using substitution
- Solve a system that represents the intersection of a circle and a line using substitution
- Solve a system that represents the intersection of a circle and an ellipse using elimination
Intersection of a Parabola and a Line
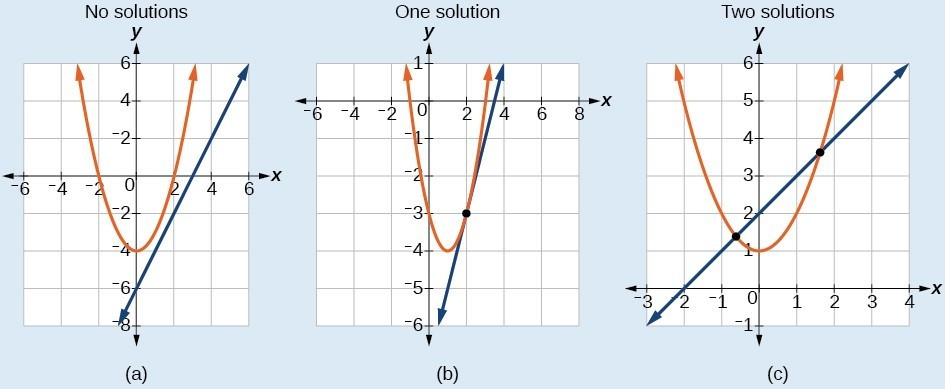
There are three possible types of solutions for a system of nonlinear equations involving a parabola and a line.A General Note: Possible Types of Solutions for Points of Intersection of a Parabola and a Line
The graphs below illustrate possible solution sets for a system of equations involving a parabola and a line.- No solution. The line will never intersect the parabola.
- One solution. The line is tangent to the parabola and intersects the parabola at exactly one point.
- Two solutions. The line crosses on the inside of the parabola and intersects the parabola at two points.
How To: Given a system of equations containing a line and a parabola, find the solution.
- Solve the linear equation for one of the variables.
- Substitute the expression obtained in step one into the parabola equation.
- Solve for the remaining variable.
- Check your solutions in both equations.
Example: Solving a System of Nonlinear Equations Representing a Parabola and a Line
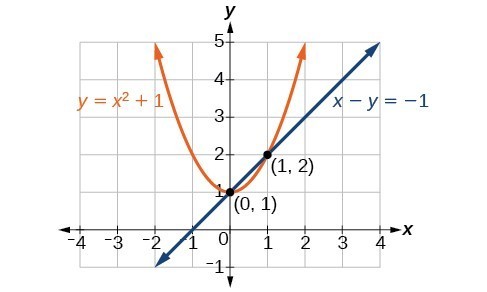
Solve the system of equations.[latex]\begin{array}{l}x-y=-1\hfill \\ y={x}^{2}+1\hfill \end{array}[/latex]
Answer: Solve the first equation for [latex]x[/latex] and then substitute the resulting expression into the second equation.
[latex]\begin{array}{llll}x-y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }x=y - 1\hfill & \hfill & \hfill & \text{Solve for }x.\hfill \\ \hfill & \hfill & \hfill & \hfill \\ \text{ }y={x}^{2}+1\hfill & \hfill & \hfill & \hfill \\ \text{ }y={\left(y - 1\right)}^{2}+1\hfill & \hfill & \hfill & \text{Substitute expression for }x.\hfill \end{array}[/latex]
Expand the equation and set it equal to zero.
[latex]\begin{array}{l}y={\left(y - 1\right)}^{2}\hfill \\ \text{ }=\left({y}^{2}-2y+1\right)+1\hfill \\ \text{ }={y}^{2}-2y+2\hfill \\ 0={y}^{2}-3y+2\hfill \\ \text{ }=\left(y - 2\right)\left(y - 1\right)\hfill \end{array}[/latex]
Solving for [latex]y[/latex] gives [latex]y=2[/latex] and [latex]y=1[/latex]. Next, substitute each value for [latex]y[/latex] into the first equation to solve for [latex]x[/latex]. Always substitute the value into the linear equation to check for extraneous solutions.
[latex]\begin{array}{l}\text{ }x-y=-1\hfill \\ x-\left(2\right)=-1\hfill \\ \text{ }x=1\hfill \\ \hfill \\ x-\left(1\right)=-1\hfill \\ \text{ }x=0\hfill \end{array}[/latex]
The solutions are [latex]\left(1,2\right)[/latex] and [latex]\left(0,1\right),\text{}[/latex] which can be verified by substituting these [latex]\left(x,y\right)[/latex] values into both of the original equations.
Q & A
Could we have substituted values for [latex]y[/latex] into the second equation to solve for [latex]x[/latex] in Example 1?
Yes, but because [latex]x[/latex] is squared in the second equation this could give us extraneous solutions for [latex]x[/latex]. For [latex]y=1[/latex][latex]\begin{array}{l}y={x}^{2}+1\hfill \\ y={x}^{2}+1\hfill \\ {x}^{2}=0\hfill \\ x=\pm \sqrt{0}=0\hfill \end{array}[/latex]
This gives us the same value as in the solution.
For [latex]y=2[/latex]
[latex]\begin{array}{l}y={x}^{2}+1\hfill \\ 2={x}^{2}+1\hfill \\ {x}^{2}=1\hfill \\ x=\pm \sqrt{1}=\pm 1\hfill \end{array}[/latex]
Notice that [latex]-1[/latex] is an extraneous solution.
Try It
Solve the given system of equations by substitution.[latex]\begin{array}{l}3x-y=-2\hfill \\ 2{x}^{2}-y=0\hfill \end{array}[/latex]
Answer: [latex]\left(-\frac{1}{2},\frac{1}{2}\right)[/latex] and [latex]\left(2,8\right)[/latex]
Solving a System of Nonlinear Equations Using Elimination
We have seen that substitution is often the preferred method when a system of equations includes a linear equation and a nonlinear equation. However, when both equations in the system have like variables of the second degree, solving them using elimination by addition is often easier than substitution. Generally, elimination is a far simpler method when the system involves only two equations in two variables (a two-by-two system), rather than a three-by-three system, as there are fewer steps. As an example, we will investigate the possible types of solutions when solving a system of equations representing a circle and an ellipse.A General Note: Possible Types of Solutions for the Points of Intersection of a Circle and an Ellipse
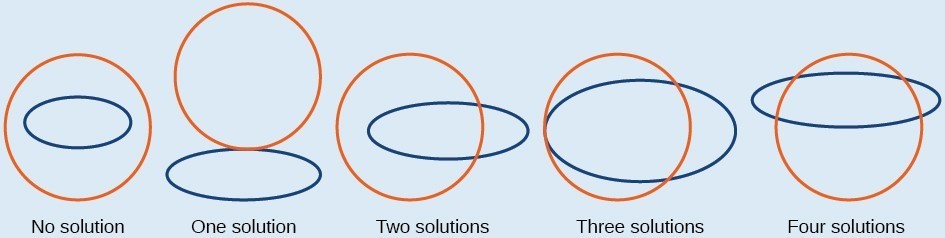
The figure below illustrates possible solution sets for a system of equations involving a circle and an ellipse.- No solution. The circle and ellipse do not intersect. One shape is inside the other or the circle and the ellipse are a distance away from the other.
- One solution. The circle and ellipse are tangent to each other, and intersect at exactly one point.
- Two solutions. The circle and the ellipse intersect at two points.
- Three solutions. The circle and the ellipse intersect at three points.
- Four solutions. The circle and the ellipse intersect at four points.
Example: Solving a System of Nonlinear Equations Representing a Circle and an Ellipse
Solve the system of nonlinear equations.[latex]\begin{array}{rr}\hfill {x}^{2}+{y}^{2}=26& \hfill \left(1\right)\\ \hfill 3{x}^{2}+25{y}^{2}=100& \hfill \left(2\right)\end{array}[/latex]
Answer: Let’s begin by multiplying equation (1) by [latex]-3,\text{}[/latex] and adding it to equation (2).
[latex]\frac{\begin{array}{l}\begin{array}{l}\hfill \\ \left(-3\right)\left({x}^{2}+{y}^{2}\right)=\left(-3\right)\left(26\right)\hfill \\ \text{ }-3{x}^{2}-3{y}^{2}=-78\hfill \end{array}\hfill \\ \text{ }3{x}^{2}+25{y}^{2}=100\hfill \end{array}}{\text{ }22{y}^{2}=22}[/latex]
After we add the two equations together, we solve for [latex]y[/latex].
[latex]\begin{array}{l}{y}^{2}=1\hfill \\ y=\pm \sqrt{1}=\pm 1\hfill \end{array}[/latex]
Substitute [latex]y=\pm 1[/latex] into one of the equations and solve for [latex]x[/latex].
[latex]\begin{array}{l}\text{ }{x}^{2}+{\left(1\right)}^{2}=26\hfill \\ \text{ }{x}^{2}+1=26\hfill \\ \text{ }{x}^{2}=25\hfill \\ \text{ }x=\pm \sqrt{25}=\pm 5\hfill \\ \hfill \\ {x}^{2}+{\left(-1\right)}^{2}=26\hfill \\ \text{ }{x}^{2}+1=26\hfill \\ \text{ }{x}^{2}=25=\pm 5\hfill \end{array}[/latex]
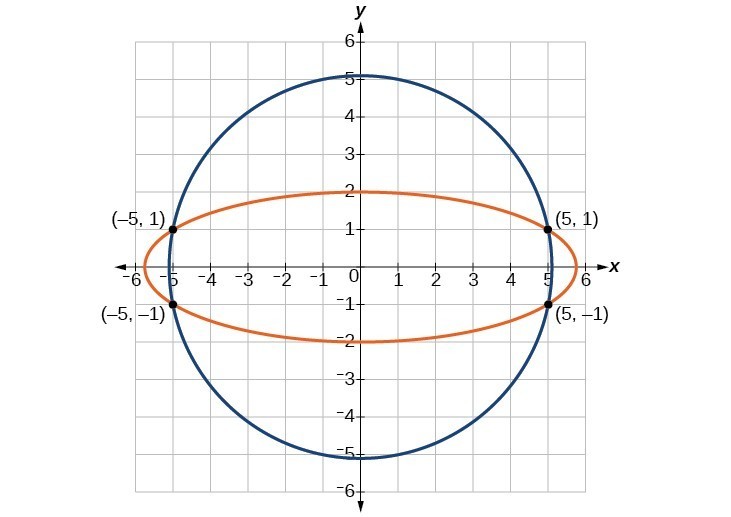
There are four solutions:
[latex]\left(5,1\right),\left(-5,1\right),\left(5,-1\right),\text{and}\left(-5,-1\right)[/latex].
Try It
Use Desmos to find the solution to the system of equations.[latex]\begin{array}{c}4{x}^{2}+{y}^{2}=13\\ {x}^{2}+{y}^{2}=10\end{array}[/latex]
Answer: [latex]\left\{\left(1,3\right),\left(1,-3\right),\left(-1,3\right),\left(-1,-3\right)\right\}[/latex]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 65041. Authored by: Etgen,Benjamin. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 62704. Authored by: Hidegkuti,Marta. License: CC BY: Attribution.
- Question ID 29703. Authored by: McClure, Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Ex 3: Solve a System of Nonlinear Equations (Elimination) . Authored by: Sousa, James (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
