Shifts
Learning Objectives
By the end of this lesson, you will be able to:- Graph functions using vertical and horizontal shifts.
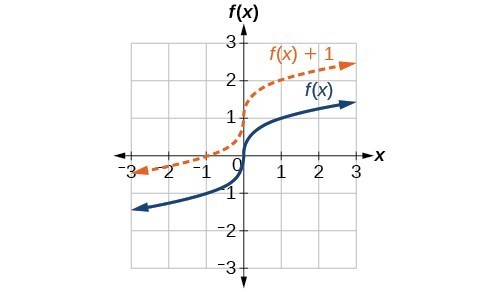 Vertical shift by [latex]k=1[/latex] of the cube root function [latex]f\left(x\right)=\sqrt[3]{x}[/latex].
Vertical shift by [latex]k=1[/latex] of the cube root function [latex]f\left(x\right)=\sqrt[3]{x}[/latex].A General Note: Vertical Shift
Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(x\right)+k[/latex], where [latex]k[/latex] is a constant, is a vertical shift of the function [latex]f\left(x\right)[/latex]. All the output values change by [latex]k[/latex] units. If [latex]k[/latex] is positive, the graph will shift up. If [latex]k[/latex] is negative, the graph will shift down.Example: Adding a Constant to a Function
To regulate temperature in a green building, airflow vents near the roof open and close throughout the day. Figure 2 shows the area of open vents [latex]V[/latex] (in square feet) throughout the day in hours after midnight, [latex]t[/latex]. During the summer, the facilities manager decides to try to better regulate temperature by increasing the amount of open vents by 20 square feet throughout the day and night. Sketch a graph of this new function.
Answer:
We can sketch a graph of this new function by adding 20 to each of the output values of the original function. This will have the effect of shifting the graph vertically up.
 Notice that for each input value, the output value has increased by 20, so if we call the new function [latex]S\left(t\right)[/latex], we could write
Notice that for each input value, the output value has increased by 20, so if we call the new function [latex]S\left(t\right)[/latex], we could write
[latex]S\left(t\right)=V\left(t\right)+20[/latex]
This notation tells us that, for any value of [latex]t,S\left(t\right)[/latex] can be found by evaluating the function [latex]V[/latex] at the same input and then adding 20 to the result. This defines [latex]S[/latex] as a transformation of the function [latex]V[/latex], in this case a vertical shift up 20 units. Notice that, with a vertical shift, the input values stay the same and only the output values change.| [latex]t[/latex] | 0 | 8 | 10 | 17 | 19 | 24 |
| [latex]V\left(t\right)[/latex] | 0 | 0 | 220 | 220 | 0 | 0 |
| [latex]S\left(t\right)[/latex] | 20 | 20 | 240 | 240 | 20 | 20 |
How To: Given a tabular function, create a new row to represent a vertical shift.
- Identify the output row or column.
- Determine the magnitude of the shift.
- Add the shift to the value in each output cell. Add a positive value for up or a negative value for down.
Example: Shifting a Tabular Function Vertically
A function [latex]f\left(x\right)[/latex] is given below. Create a table for the function [latex]g\left(x\right)=f\left(x\right)-3[/latex].| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]f\left(x\right)[/latex] | 1 | 3 | 7 | 11 |
Answer: The formula [latex]g\left(x\right)=f\left(x\right)-3[/latex] tells us that we can find the output values of [latex]g[/latex] by subtracting 3 from the output values of [latex]f[/latex]. For example:
[latex]\begin{cases}f\left(2\right)=1\hfill & \text{Given}\hfill \\ g\left(x\right)=f\left(x\right)-3\hfill & \text{Given transformation}\hfill \\ g\left(2\right)=f\left(2\right)-3\hfill & \hfill \\ =1 - 3\hfill & \hfill \\ =-2\hfill & \hfill \end{cases}[/latex]
Subtracting 3 from each [latex]f\left(x\right)[/latex] value, we can complete a table of values for [latex]g\left(x\right)[/latex].| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]f\left(x\right)[/latex] | 1 | 3 | 7 | 11 |
| [latex]g\left(x\right)[/latex] | −2 | 0 | 4 | 8 |
Analysis of the Solution
As with the earlier vertical shift, notice the input values stay the same and only the output values change.Identifying Horizontal Shifts
We just saw that the vertical shift is a change to the output, or outside, of the function. We will now look at how changes to input, on the inside of the function, change its graph and meaning. A shift to the input results in a movement of the graph of the function left or right in what is known as a horizontal shift. Horizontal shift of the function [latex]f\left(x\right)=\sqrt[3]{x}[/latex]. Note that [latex]h=+1[/latex] shifts the graph to the left, that is, towards negative values of [latex]x[/latex].
Horizontal shift of the function [latex]f\left(x\right)=\sqrt[3]{x}[/latex]. Note that [latex]h=+1[/latex] shifts the graph to the left, that is, towards negative values of [latex]x[/latex].A General Note: Horizontal Shift
Given a function [latex]f[/latex], a new function [latex]g\left(x\right)=f\left(x-h\right)[/latex], where [latex]h[/latex] is a constant, is a horizontal shift of the function [latex]f[/latex]. If [latex]h[/latex] is positive, the graph will shift right. If [latex]h[/latex] is negative, the graph will shift left.Example: Adding a Constant to an Input
Returning to our building airflow example from Example 2, suppose that in autumn the facilities manager decides that the original venting plan starts too late, and wants to begin the entire venting program 2 hours earlier. Sketch a graph of the new function.Answer: We can set [latex]V\left(t\right)[/latex] to be the original program and [latex]F\left(t\right)[/latex] to be the revised program.
[latex]\begin{cases}{c}V\left(t\right)=\text{ the original venting plan}\\ \text{F}\left(t\right)=\text{starting 2 hrs sooner}\end{cases}[/latex]
In the new graph, at each time, the airflow is the same as the original function [latex]V[/latex] was 2 hours later. For example, in the original function [latex]V[/latex], the airflow starts to change at 8 a.m., whereas for the function [latex]F[/latex], the airflow starts to change at 6 a.m. The comparable function values are [latex]V\left(8\right)=F\left(6\right)[/latex]. Notice also that the vents first opened to [latex]220{\text{ ft}}^{2}[/latex] at 10 a.m. under the original plan, while under the new plan the vents reach [latex]220{\text{ ft}}^{\text{2}}[/latex] at 8 a.m., so [latex]V\left(10\right)=F\left(8\right)[/latex]. In both cases, we see that, because [latex]F\left(t\right)[/latex] starts 2 hours sooner, [latex]h=-2[/latex]. That means that the same output values are reached when [latex]F\left(t\right)=V\left(t-\left(-2\right)\right)=V\left(t+2\right)[/latex].
In both cases, we see that, because [latex]F\left(t\right)[/latex] starts 2 hours sooner, [latex]h=-2[/latex]. That means that the same output values are reached when [latex]F\left(t\right)=V\left(t-\left(-2\right)\right)=V\left(t+2\right)[/latex].
Analysis of the Solution
Note that [latex]V\left(t+2\right)[/latex] has the effect of shifting the graph to the left. Horizontal changes or "inside changes" affect the domain of a function (the input) instead of the range and often seem counterintuitive. The new function [latex]F\left(t\right)[/latex] uses the same outputs as [latex]V\left(t\right)[/latex], but matches those outputs to inputs 2 hours earlier than those of [latex]V\left(t\right)[/latex]. Said another way, we must add 2 hours to the input of [latex]V[/latex] to find the corresponding output for [latex]F:F\left(t\right)=V\left(t+2\right)[/latex].Example: Identifying a Horizontal Shift of a Toolkit Function
This graph represents a transformation of the toolkit function [latex]f\left(x\right)={x}^{2}[/latex]. Relate this new function [latex]g\left(x\right)[/latex] to [latex]f\left(x\right)[/latex], and then find a formula for [latex]g\left(x\right)[/latex].
Answer: Notice that the graph is identical in shape to the [latex]f\left(x\right)={x}^{2}[/latex] function, but the x-values are shifted to the right 2 units. The vertex used to be at (0,0), but now the vertex is at (2,0). The graph is the basic quadratic function shifted 2 units to the right, so
[latex]g\left(x\right)=f\left(x - 2\right)[/latex]
Notice how we must input the value [latex]x=2[/latex] to get the output value [latex]y=0[/latex]; the x-values must be 2 units larger because of the shift to the right by 2 units. We can then use the definition of the [latex]f\left(x\right)[/latex] function to write a formula for [latex]g\left(x\right)[/latex] by evaluating [latex]f\left(x - 2\right)[/latex].[latex]\begin{cases}f\left(x\right)={x}^{2}\hfill \\ g\left(x\right)=f\left(x - 2\right)\hfill \\ g\left(x\right)=f\left(x - 2\right)={\left(x - 2\right)}^{2}\hfill \end{cases}[/latex]
Analysis of the Solution
To determine whether the shift is [latex]+2[/latex] or [latex]-2[/latex] , consider a single reference point on the graph. For a quadratic, looking at the vertex point is convenient. In the original function, [latex]f\left(0\right)=0[/latex]. In our shifted function, [latex]g\left(2\right)=0[/latex]. To obtain the output value of 0 from the function [latex]f[/latex], we need to decide whether a plus or a minus sign will work to satisfy [latex]g\left(2\right)=f\left(x - 2\right)=f\left(0\right)=0[/latex]. For this to work, we will need to subtract 2 units from our input values.Try It
Desmos can graph transformations using function notation. Use Desmos to graph the toolkit function [latex]f(x) = x^2[/latex] Now, enter [latex]f(x+5)[/latex], and [latex]f(x)+5[/latex] in the next two lines.Answer: You have graphed the following transformations: [latex-display]f(x+3)=(x+3)^2[/latex-display] [latex-display]f(x)+3=(x)^2+3[/latex-display]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 113437, 60789. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 75586, 75929, 75931. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 33066. Authored by: Smart, Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
