We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Introduction to Factoring

Learning Outcomes

  • Use the principle of zero products to solve equations
  • Determine for what kind of equations the principle of zero products can be used
  • Explain why some techniques for solving linear equations don't work for solving polynomial equations
  Consider the profit equation for a cell phone manufacturer:

[latex]P=-0.09x^2+5000x-750,000[/latex]

Using an online graphing calculator, we generated this graph of the profit equation.

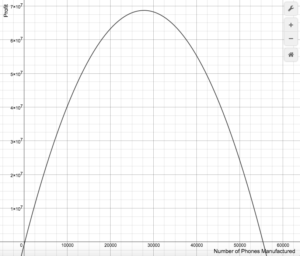Screen Shot 2016-06-07 at 2.42.59 PM A manager may want to know for what amount of phones manufactured and sold will a profit be made.  By substituting 100 in for x, we discovered that when 100 phones were manufactured and sold, the company did not make a profit. Substitute x = 100

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\=-0.09\left(100\right)^2+5000\left(100\right)-750,000\\=-900+500,000-750,000\\=-250,900\end{array}[/latex]

Finding the points where profit is greater than or equal to zero will guide management decisions, and help the company plan to have enough labor and materials on hand. Knowing where profit equals zero gives the company a baseline from which to plan. On the graph, profit is zero when the parabola crosses the x-axis. In algebraic terms, this means finding where the profit equation is equal to zero:

[latex]\begin{array}{c}P=-0.09x^2+5000x-750,000\\0=-0.09x^2+5000x-750,000\\0<-0.09x^2+5000x-750,000\end{array}[/latex]

We know how to solve linear equations like this: [latex]x-4=0[/latex], and linear inequalities like this: [latex]x-4>0[/latex].  But, how do you solve a polynomial equation like this: [latex]0=-0.09x^2+5000x-750,000[/latex], or an inequality like this: [latex]0<-0.09x^2+5000x-750,000[/latex]?

In this section we will learn some very useful tools for solving certain kinds of polynomial equations, and in later math courses you will likely learn how to extend these ideas to solving polynomial inequalities. The first concept we will explore is that of the zero product property, then we will discuss how that can be used to solve polynomial equations.

The Principle of Zero Products

The number zero Zero
What if we told you that we multiplied two numbers together and got an answer of zero? What could you say about the two numbers? Could they be 2 and 5? Could they be 9 and 1? No! When the result (answer) from multiplying two numbers is zero, that means that one of them had to be zero. This idea is called the zero product principle, and it is useful for solving certain kinds of equations, like we described in the cell phone manufacturer example.      

Principle of Zero Products

The Principle of Zero Products states that if the product of two numbers is 0, then at least one of the factors is 0. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are 0.
 

Example

Use the principle of zero products to solve. [latex]5y=0[/latex]

Answer: By the principle of zero products, when two factors are multiplied and the result is zero at least one of them is equal to zero.  Therefore, either [latex]5=0[/latex], or [latex]y=0[/latex]. In this case, we know that 5 is not equal to zero, so [latex]y[/latex] must be equal to zero. We can verify this with algebra.

[latex]\begin{array}{c}5y=0\\\text{}\\\frac{5y}{5}=\frac{0}{5}\\\text{}\\y=0\end{array}[/latex]

Answer

Both by the principle of  zero products, and with algebra, we have shown that [latex]y=0[/latex].

We can extend this idea to products of more than just two numbers.  In the next example we will show that we can use the principle of zero products to solve an equation containing the product of a number and a binomial.

Example

Use the principle of zero products to solve: [latex-display]7\left(y-2\right)=0[/latex-display]

Answer: By the principle of zero products, either [latex]7 = 0[/latex], or [latex]\left(y-2\right)=0[/latex].  We know that [latex]7\neq0[/latex], so we are left with [latex]\left(y-2\right)=0[/latex].  We know how to solve this kind of equation! We can remove the parentheses because they are not needed to solve.

[latex]\begin{array}{c}y-2=0\\\,\,\,\,\,\,\,\,\,\underline{+2}\,\,\,\,\,\,\underline{+2}\\\text{}\\\,\,\,\,\,\,\,\,\,\,y=2\end{array}[/latex]

We can check this is correct by substituting 2 for y into the original equation.

[latex]\begin{array}{c}7\left(2-2\right)=0\\7\left(0\right)=0\\0=0\end{array}[/latex]

This statement is true, so we have found the correct value for y.

Answer

[latex]y=2[/latex]

We could have used the distributive property and the addition and multiplication properties of equality to solve the equation in the previous example. It would look something like this: Solve [latex]7\left(y-2\right)=0[/latex] using the distributive property.

[latex]\begin{array}{c}7\left(y-2\right)=0\\7y-14=0\\\,\,\,\,\,\,\,\,\,\underline{+14}\,\,\,\,\,\,\underline{+14}\\\text{}\\7y=14\\\text{}\\\frac{7y}{7}=\frac{14}{7}\\\text{}\\y=2\end{array}[/latex]

We have the same answer that we verified in the example, but we used different algebraic principles to find it.

In the next example we add another layer to the idea that we can use the principle of zero products to solve equations. We will solve an equation that contains the product of a variable and a binomial.

Example

Use the principle of zero products to solve: [latex-display]t\left(5-t\right)=0[/latex-display]

Answer: By the principle of zero products, either [latex]t=0[/latex] or [latex]\left(5-t\right)=0[/latex] [latex-display]\displaystyle\begin{array}{c}t=0\,\,\,\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,\,\,5-t=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-5}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-t=-5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-t}{-1}=\frac{-5}{-1}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=5\\\text{}\\t=0\,\,\,\,\,\,\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t=5\end{array}[/latex-display] Wow, two answers!  Let's check that they are both correct. Substitute [latex]t=0[/latex]

[latex]\begin{array}{c}t\left(5-t\right)=0\\0\left(5-0\right)=0\\\,\,\,\,\,\,\,\,\,\,0\left(5\right)=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0=0\end{array}[/latex]

[latex-display]t=0[/latex] checks, now let's check [latex]t=5[/latex-display] Substitute [latex]t=5[/latex]

[latex]\begin{array}{c}5\left(5-5\right)=0\\\,\,\,\,\,\,\,\,\,\,\,5\left(0\right)=0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0=0\end{array}[/latex]

 [latex]t=5[/latex] also checks.  There are two answers to this equation.

Answer

[latex-display]t=0\text{ OR }t=5[/latex-display]

Why don't we just use the distributive property to solve these kind of equations? Let's try using the distributive property on the previous example to explain why this will not always work.

[latex]\begin{array}{c}t\left(5-t\right)=0\\\text{}\\5t-t^2=0\\\underline{-5t}\,\,\,\,\,\,\,\,\,\,\underline{-5t}\\t^2=-5t\\\text{}\\t\cdot{t}=-5t\\\text{}\\\frac{t\cdot{t}}{t}=\frac{-5t}{t}\\\text{}\\t=-5\end{array}[/latex]

Wait, in the example, our solution was [latex]t=0\text{ OR }t=5[/latex].  Let's check this new answer to see if it is correct. Substitute [latex]t=-5[/latex]

[latex]\begin{array}{c}-5\left(5-\left(-5\right)\right)=0\\-5\left(5+5\right)=0\\-5\left(10\right)=0\\-50\neq{0}\end{array}[/latex]

This isn't even the right answer!

When we are solving polynomial equations, we need to use some different methods than we used to solve linear equations to make sure we get all of the correct answers.  The principle of zero products is one tool that allows us to do this.

CautionCaution!  It is important to remember that the principle of zero products only works when we have an equation with zero on one side, and only a product on the other side. The table below gives examples of equations for which you can and cannot apply the principle of zero products.
YES Zero Products Works to Solve NO Zero Products Does Not Work to Solve WHY NOT?
[latex]\frac{1}{2}\left(x-2\right)=0[/latex] [latex]\frac{1}{2}\left(x-2\right)=28[/latex] There is a product on the left, but it is not equal to zero.
[latex]s\left(9+s\right)=0[/latex] [latex]s^2+9s=0[/latex] There is a sum equal to zero but no product equal to zero.
Let's look at one more example of how the principle of zero products can be used to solve equations involving products that are binomials.

Example

Use the principle of zero products to solve: [latex-display]\left(s+1\right)\left(s-5\right)=0[/latex-display]

Answer: Set both products equal to zero, then solve the linear equations. [latex-display]\begin{array}{c}\left(s+1\right)=0\\s+1=0\\\underline{-1}\,\,\,\,\,\,\,\underline{-1}\\s=-1\end{array}[/latex-display] [latex-display]\begin{array}{c}\left(s-5\right)=0\\s-5=0\\\,\,\,\,\,\,\,\,\,\,\,\underline{+5}\,\,\,\,\,\underline{+5}\\\,\,\,\,\,\,\,\,\,s=5\end{array}[/latex-display]

Answer

[latex-display]s=-1\text{ OR }s=5[/latex-display]

The last two examples we showed were both polynomial equations that were degree two. Remember that degree means the largest exponent in the polynomial. Degree two polynomials are often called quadratic.  Using the distributive property to multiply the products in the last example will help you see that it is a degree two polynomial. Use a table:
[latex]s[/latex] [latex]+1[/latex]
[latex]s[/latex] [latex]s^2[/latex] [latex]s[/latex]
[latex]-5[/latex] [latex]-5s[/latex]  [latex]-5[/latex]
Combine terms and simplify: [latex-display]\begin{array}{c}s^2+s-5s-5\\=s^2-4s-5\end{array}[/latex-display] When the polynomial is simplified, you can tell that it is a degree two polynomial, or a quadratic polynomial. At the start of this page, we proposed that a business would be interested in where the quadratic polynomial that represented profit was equal to or greater than zero.  We have presented one way to find where a quadratic polynomial is equal to zero, as long as it is in the form of a product of two binomials, and hasn't been multiplied out. In the following video we present more examples of how to use the zero product principle to solve polynomial equations that are in factored form. https://youtu.be/yCcMCPHFrVc What would you do if you were asked to solve a quadratic equation such as [latex]y^2+2y=0[/latex]? We have already shown that we can't use the same techniques we used to solve linear equations.  In the next section, we will show you how to re-write [latex]y^2+2y=0[/latex] as the product of a monomial and a binomial so you can use the zero product principle to solve it.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Ex: Solve an Equation in Factored Form. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.