Graph Quadratic Functions
Learning Outcomes
- Graph quadratic functions using tables and transformations
- Identify important features of the graphs of quadratic functions
| x | f(x) |
|---|---|
| [latex]−2[/latex] | [latex]4[/latex] |
| [latex]−1[/latex] | [latex]1[/latex] |
| [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]1[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
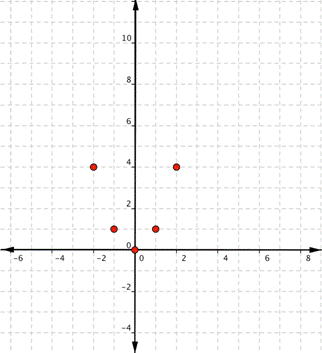Since the points are not on a line, you cannot use a straight edge. Connect the points as best as you can using a smooth curve (not a series of straight lines). You may want to find and plot additional points (such as the ones in blue here). Placing arrows on the tips of the lines implies that they continue in that direction forever.
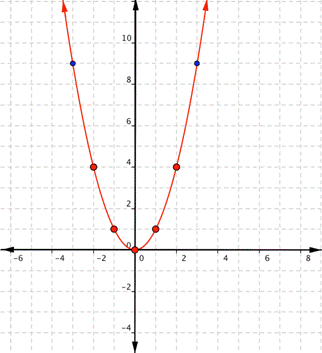Notice that the shape is similar to the letter U. This is called a parabola. One-half of the parabola is a mirror image of the other half. The lowest point on this graph is called the vertex. The vertical line that goes through the vertex is called the line of reflection. In this case, that line is the y-axis.
The equations for quadratic functions have the form [latex]f(x)=ax^{2}+bx+c[/latex] where [latex] a\ne 0[/latex]. In the basic graph above, [latex]a=1[/latex], [latex]b=0[/latex], and [latex]c=0[/latex].
In the following video, we show an example of plotting a quadratic function using a table of values.
https://youtu.be/wYfEzOJugS8
Changing a changes the width of the parabola and whether it opens up ([latex]a>0[/latex]) or down ([latex]a<0[/latex]). If a is positive, the vertex is the lowest point, if a is negative, the vertex is the highest point. In the following example, we show how changing the value of a will affect the graph of the function.
Example
Match each function with its graph. a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] 1)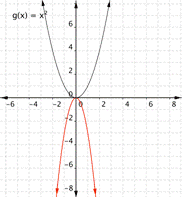
2)
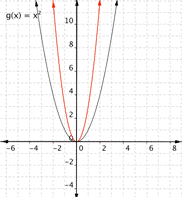3)
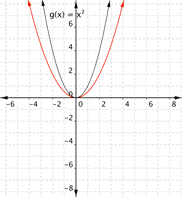
Answer:
Function a) matches graph [latex]2[/latex]
Function b) matches graph [latex]1[/latex]
Function c) matches graph [latex]3[/latex]
Function a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by three, so the outputs will be greater than they would have been for [latex]f(x)=x^2[/latex]. This results in a parabola that has been squeezed, so graph [latex]2[/latex] is the best match for this function.
Function b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by negative three, so the outputs will be farther away from the [latex]x[/latex]-axis than they would have been for [latex]f(x)=x^2[/latex], but negative in value, so graph [latex]1[/latex] is the best match for this function.
Function c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] means that inputs are squared then multiplied by [latex]\dfrac{1}{2}[/latex], so the outputs are less than they would be for [latex]f(x)=x^2[/latex]. This results in a parabola that has been opened wider than[latex]f(x)=x^2[/latex]. Graph [latex]3[/latex] is the best match for this function.
Example
Match each of the following functions with its graph. a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex] 1)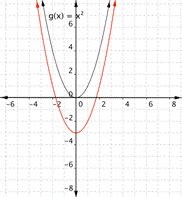
2)
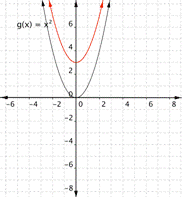
Answer:
Function a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] means square the inputs then add three, so every output will be moved up [latex]3[/latex] units. The graph that matches this function best is [latex]2[/latex].
Function b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex] means square the inputs then subtract three, so every output will be moved down [latex]3[/latex] units. The graph that matches this function best is [latex]1[/latex].
Example
Match each of the following functions with its graph. a) [latex] \displaystyle f(x)={{x}^{2}}+2x[/latex] b) [latex] \displaystyle f(x)={{x}^{2}}-2x[/latex] a)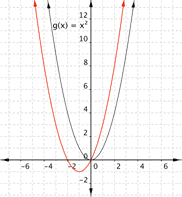
b)
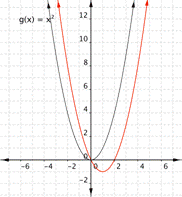
Answer:
Find the vertex of function a)
[latex] \displaystyle f(x)={{x}^{2}}+2x[/latex].
[latex-display]a = 1, b = 2[/latex-display]
x-value:
[latex-display]\dfrac{-b}{2a}=\dfrac{-2}{2(1)}=-1[/latex-display]
y-value:
[latex]f(\dfrac{-b}{2a})=(-1)^2+2(-1)=1-2=-1[/latex].
Vertex = [latex](-1,-1)[/latex], which means the graph that best fits this function is a)
Find the vertex of function b)
[latex]f(x)={{x}^{2}}-2x[/latex].
[latex-display]a = 1, b = -2[/latex-display]
x-value:
[latex-display]\dfrac{-b}{2a}=\dfrac{2}{2(1)}=1[/latex-display]
y-value:
[latex]f(\dfrac{-b}{2a})=(1)^2-2(1)=1-2=-1[/latex].
Vertex = [latex](1,-1)[/latex], which means the graph that best fits this function is b)
Properties of a Parabola
For [latex] \displaystyle f(x)=a{{x}^{2}}+bx+c[/latex], where a, b, and c are real numbers,- The parabola opens upward if [latex]a > 0[/latex] and downward if [latex]a < 0[/latex].
- a changes the width of the parabola. The parabola gets narrower if [latex]|a|> 1[/latex] and wider if [latex]|a|<1[/latex].
- The vertex depends on the values of a, b, and c. The vertex is [latex]\left(\dfrac{-b}{2a},f\left( \dfrac{-b}{2a}\right)\right)[/latex].
Example
Graph [latex]f(x)=−2x^{2}+3x–3[/latex].Answer: Before making a table of values, look at the values of a and c to get a general idea of what the graph should look like. [latex]a=−2[/latex], so the graph will open down and be thinner than [latex]f(x)=x^{2}[/latex]. [latex]c=−3[/latex], so it will move to intersect the y-axis at [latex](0,−3)[/latex]. To find the vertex of the parabola, use the formula [latex] \displaystyle \left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]. Finding the vertex may make graphing the parabola easier.
[latex]\text{Vertex }\text{formula}=\left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]
x-coordinate of vertex:[latex] \displaystyle \dfrac{-b}{2a}=\dfrac{-(3)}{2(-2)}=\dfrac{-3}{-4}=\dfrac{3}{4}[/latex]
y-coordinate of vertex:[latex] \displaystyle \begin{array}{l}f\left( \dfrac{-b}{2a} \right)=f\left( \dfrac{3}{4} \right)\\\,\,\,f\left( \dfrac{3}{4} \right)=-2{{\left( \dfrac{3}{4} \right)}^{2}}+3\left( \dfrac{3}{4} \right)-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-2\left( \dfrac{9}{16} \right)+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-18}{16}+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-9}{8}+\dfrac{18}{8}-\dfrac{24}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\dfrac{15}{8}\end{array}[/latex]
Vertex: [latex] \displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex] Use the vertex, [latex] \displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex], and the properties you described to get a general idea of the shape of the graph. You can create a table of values to verify your graph. Notice that in this table, the x values increase. The y values increase and then start to decrease again. This indicates a parabola.| x | f(x) |
|---|---|
| [latex]−2[/latex] | [latex]−17[/latex] |
| [latex]−1[/latex] | [latex]−8[/latex] |
| [latex]0[/latex] | [latex]−3[/latex] |
| [latex]1[/latex] | [latex]−2[/latex] |
| [latex]2[/latex] | [latex]−5[/latex] |
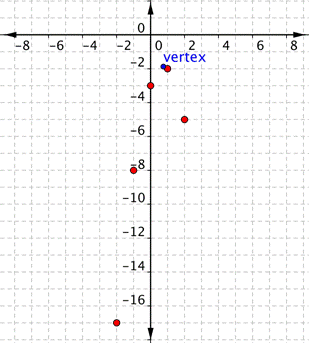Connect the points as best you can using a smooth curve. Remember that the parabola is two mirror images, so if your points do not have pairs with the same value, you may want to include additional points (such as the ones in blue shown below). Plot points on either side of the vertex.
[latex]x=\dfrac{1}{2}[/latex] and [latex]x=\dfrac{3}{2}[/latex] are good values to include.
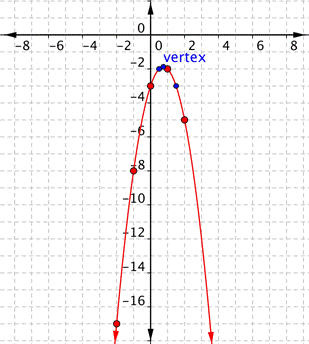
Summary
Creating a graph of a function is one way to understand the relationship between the inputs and outputs of that function. Creating a graph can be done by choosing values for x, finding the corresponding y values, and plotting them. However, it helps to understand the basic shape of the function. Knowing how changes to the basic function equation affect the graph is also helpful. The shape of a quadratic function is a parabola. Parabolas have the equation [latex]f(x)=ax^{2}+bx+c[/latex], where a, b, and c are real numbers and [latex]a\ne0[/latex]. The value of a determines the width and the direction of the parabola, while the vertex depends on the values of a, b, and c. The vertex is [latex] \displaystyle \left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex].Licenses & Attributions
CC licensed content, Original
- Graph a Quadratic Function Using a Table of Value and the Vertex. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Graph a Quadratic Function Using a Table of Values. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
