We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Dividing Fractions

Learning Outcomes

  • Find the reciprocal of a number
  • Divide a fraction by a whole number
  • Divide a fraction by a fraction

Divide Fractions

There are times when you need to use division to solve a problem. For example, if painting one coat of paint on the walls of a room requires [latex]3[/latex] quarts of paint and you have a bucket that contains [latex]6[/latex] quarts of paint, how many coats of paint can you paint on the walls? You divide [latex]6[/latex] by [latex]3[/latex] for an answer of [latex]2[/latex] coats. There will also be times when you need to divide by a fraction. Suppose painting a closet with one coat only required [latex]\dfrac{1}{2}[/latex] quart of paint. How many coats could be painted with the 6 quarts of paint? To find the answer, you need to divide [latex]6[/latex] by the fraction, [latex]\dfrac{1}{2}[/latex]. Before we begin dividing fractions, let's cover some important terminology.
  • reciprocal: two fractions are reciprocals if their product is [latex]1[/latex] (Don't worry; we will show you examples of what this means.)
  • quotient: the result of division
Dividing fractions requires using the reciprocal of a number or fraction. If you multiply two numbers together and get [latex]1[/latex] as a result, then the two numbers are reciprocals. Here are some examples of reciprocals:
Original number Reciprocal Product
[latex]\dfrac{3}{4}[/latex] [latex]\dfrac{4}{3}[/latex] [latex]\dfrac{3}{4}\cdot\dfrac{4}{3}=\dfrac{3\cdot 4}{4\cdot 3}=\dfrac{12}{12}=1[/latex]
[latex]\dfrac{1}{2}[/latex] [latex]\dfrac{2}{1}[/latex] [latex]\dfrac{1}{2}\cdot\dfrac{2}{1}=\dfrac{1\cdot2}{2\cdot1}=\dfrac{2}{2}=1[/latex]
[latex] 3=\dfrac{3}{1}[/latex] [latex]\dfrac{1}{3}[/latex] [latex]\dfrac{3}{1}\cdot\dfrac{1}{3}=\dfrac{3\cdot 1}{1\cdot 3}=\dfrac{3}{3}=1[/latex]
[latex]2\dfrac{1}{3}=\dfrac{7}{3}[/latex] [latex]\dfrac{3}{7}[/latex] [latex]\dfrac{7}{3}\cdot\dfrac{3}{7}=\dfrac{7\cdot3}{3\cdot7}=\dfrac{21}{21}=\normalsize 1[/latex]
You can think of it as switching the numerator and denominator: swap the [latex]2[/latex] with the [latex]5[/latex] in [latex]\dfrac{2}{5}[/latex] to get the reciprocal [latex]\dfrac{5}{2}[/latex]. Make sure that if it's a negative fraction, the reciprocal is also negative. This is because the product of two negative numbers will give you the positive one that you are looking for.

Division by Zero

You know what it means to divide by [latex]2[/latex] or divide by [latex]10[/latex], but what does it mean to divide a quantity by [latex]0[/latex]? Is this even possible? On the flip side, can you divide [latex]0[/latex] by a number? Consider the fraction

[latex]\dfrac{0}{8}[/latex]

We can read it as, “zero divided by eight.” Since multiplication is the inverse of division, we could rewrite this as a multiplication problem. What number times [latex]8[/latex] equals [latex]0[/latex]?

[latex]\text{?}\cdot{8}=0[/latex]

We can infer that the unknown must be [latex]0[/latex] since that is the only number that will give a result of [latex]0[/latex] when it is multiplied by [latex]8[/latex].

Now let’s consider the reciprocal of [latex]\dfrac{0}{8}[/latex] which would be [latex]\dfrac{8}{0}[/latex]. If we rewrite this as a multiplication problem, we will have "what times [latex]0[/latex] equals [latex]8[/latex]?"

[latex]\text{?}\cdot{0}=8[/latex]

This doesn't make any sense. There are no numbers that you can multiply by zero to get a result of 8. In fact, any number divided by [latex]0[/latex] is impossible, or better defined, all division by zero is undefined.
CautionCaution! Division by zero is undefined and so is the reciprocal of any fraction that has a zero in the numerator. For any real number a, [latex]\dfrac{a}{0}[/latex] is undefined. Additionally, the reciprocal of [latex]\dfrac{0}{a}[/latex] will always be undefined.

Divide a Fraction by a Whole Number

When you divide by a whole number, you are also multiplying by the reciprocal. In the painting example where you need [latex]3[/latex] quarts of paint for a coat and have [latex]6[/latex] quarts of paint, you can find the total number of coats that can be painted by dividing [latex]6[/latex] by [latex]3[/latex], [latex]6\div3=2[/latex]. You can also multiply [latex]6[/latex] by the reciprocal of [latex]3[/latex], which is [latex]\dfrac{1}{3}[/latex], so the multiplication problem becomes

[latex]\dfrac{6}{1}\cdot\dfrac{1}{3}=\dfrac{6}{3}=\normalsize2[/latex]

Dividing is Multiplying by the Reciprocal

For all division, you can turn the operation into multiplication by using the reciprocal. Dividing is the same as multiplying by the reciprocal.
The same idea will work when the divisor (the thing being divided) is a fraction. If you have a recipe that needs to be divided in half, you can divide each ingredient by [latex]2[/latex], or you can multiply each ingredient by [latex]\dfrac{1}{2}[/latex] to find the new amount. If you have [latex]\dfrac{3}{4}[/latex] of a candy bar and need to divide it among [latex]5[/latex] people, each person gets [latex]\dfrac{1}{5}[/latex] of the available candy:

[latex]\dfrac{1}{5}\normalsize\text{ of }\dfrac{3}{4}=\dfrac{1}{5}\cdot\dfrac{3}{4}=\dfrac{3}{20}[/latex]

Each person gets [latex]\dfrac{3}{20}[/latex] of a whole candy bar.

  For example, dividing by [latex]6[/latex] is the same as multiplying by the reciprocal of [latex]6[/latex], which is [latex]\dfrac{1}{6}[/latex]. Look at the diagram of two pizzas below.  How can you divide what is left (the red shaded region) among [latex]6[/latex] people fairly?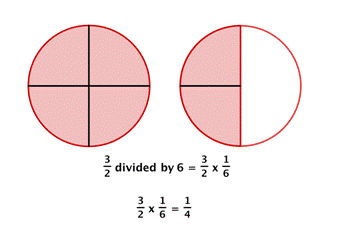 Two pizzas divided into fourths. One pizza has all four pieces shaded, and the other pizza has two of the four slices shaded. 3/2 divided by 6 is equal to 3/2 times 1/6. This is 3/2 times 1/6 equals 1/4. Each person gets one piece, so each person gets [latex]\dfrac{1}{4}[/latex] of a pizza. Dividing a fraction by a whole number is the same as multiplying by the reciprocal, so you can always use multiplication of fractions to solve division problems.

Example

Find [latex]\dfrac{2}{3}\div \normalsize 4[/latex]

Answer: Write your answer in lowest terms. Dividing by [latex]4[/latex] or [latex]\dfrac{4}{1}[/latex] is the same as multiplying by the reciprocal of [latex]4[/latex], which is [latex]\dfrac{1}{4}[/latex].

[latex]\dfrac{2}{3}\normalsize\div 4=\dfrac{2}{3}\cdot\dfrac{1}{4}[/latex]

Multiply numerators and multiply denominators.

[latex]\dfrac{2\cdot 1}{3\cdot 4}=\dfrac{2}{12}[/latex]

Simplify to lowest terms by dividing numerator and denominator by the common factor [latex]4[/latex].

[latex]\dfrac{1}{6}[/latex]

Answer

[latex-display]\dfrac{2}{3}\div4=\dfrac{1}{6}[/latex-display]

Example

Divide. [latex] 9\div\dfrac{1}{2}[/latex]

Answer: Write your answer in lowest terms. Dividing by [latex]\dfrac{1}{2}[/latex] is the same as multiplying by the reciprocal of [latex]\dfrac{1}{2}[/latex], which is [latex]\dfrac{2}{1}[/latex].

[latex]9\div\dfrac{1}{2}=\dfrac{9}{1}\cdot\dfrac{2}{1}[/latex]

Multiply numerators and multiply denominators.

[latex]\dfrac{9\cdot 2}{1\cdot 1}=\dfrac{18}{1}=\normalsize 18[/latex]

This answer is already simplified to lowest terms.

Answer

[latex-display]9\div\dfrac{1}{2}=\normalsize 18[/latex-display]

Divide a Fraction by a Fraction

Sometimes you need to solve a problem that requires dividing by a fraction. Suppose you have a pizza that is already cut into [latex]4[/latex] slices. How many [latex]\dfrac{1}{2}[/latex] slices are there?
A pizza divided into four equal pieces. There are four slices. A pizza divided into four equal slices. Each slice is then divided in half. There are now 8 slices.
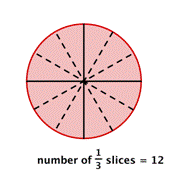There are [latex]8[/latex] slices. You can see that dividing [latex]4[/latex] by [latex]\dfrac{1}{2}[/latex] gives the same result as multiplying [latex]4[/latex] by [latex]2[/latex]. What would happen if you needed to divide each slice into thirds? A pizza divided into four equal slice. Each slice is divided into thirds. There are now 12 slices. You would have [latex]12[/latex] slices, which is the same as multiplying [latex]4[/latex] by [latex]3[/latex].

Dividing with Fractions

  1. Find the reciprocal of the number that follows the division symbol.
  2. Multiply the first number (the one before the division symbol) by the reciprocal of the second number (the one after the division symbol).
Any easy way to remember how to divide fractions is the phrase “keep, change, flip.” This means to KEEP the first number, CHANGE the division sign to multiplication, and then FLIP (use the reciprocal) of the second number.

Example

Divide [latex]\dfrac{2}{3}\div\dfrac{1}{6}[/latex]

Answer: Multiply by the reciprocal. KEEP [latex]\dfrac{2}{3}[/latex] CHANGE  [latex] \div [/latex] to  [latex]\cdot[/latex] FLIP  [latex]\dfrac{1}{6}[/latex]

[latex]\dfrac{2}{3}\cdot\dfrac{6}{1}[/latex]

Multiply numerators and multiply denominators.

[latex]\dfrac{2\cdot6}{3\cdot1}=\dfrac{12}{3}[/latex]

Simplify.

[latex]\dfrac{12}{3}=\normalsize 4[/latex]

Answer

[latex-display]\dfrac{2}{3}\div\dfrac{1}{6}=4[/latex-display]

Example

Divide [latex]\dfrac{3}{5}\div\dfrac{2}{3}[/latex]

Answer: Multiply by the reciprocal. Keep [latex]\dfrac{3}{5}[/latex], change [latex] \div [/latex] to [latex]\cdot[/latex], and flip [latex]\dfrac{2}{3}[/latex].

[latex]\dfrac{3}{5}\cdot\dfrac{3}{2}[/latex]

Multiply numerators and multiply denominators.

[latex]\dfrac{3\cdot 3}{5\cdot 2}=\dfrac{9}{10}[/latex]

Answer

[latex-display]\dfrac{3}{5}\div\dfrac{2}{3}=\dfrac{9}{10}[/latex-display]

When solving a division problem by multiplying by the reciprocal, remember to write all whole numbers and mixed numbers as improper fractions before doing calculations  [latex](\text{i.e. } 5=\dfrac{5}{1}[/latex]  and  [latex]1\dfrac{3}{4}=\dfrac{7}{4})[/latex]. The final answer should always be simplified and written as a mixed number if larger than [latex]1[/latex]. In the following video you will see an example of how to divide an integer by a fraction, as well as an example of how to divide a fraction by another fraction. https://youtu.be/F5YSNLel3n8

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Ex 1: Divide Fractions (Basic). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Located at: https://openstax.org/books/prealgebra/pages/4-2-multiply-and-divide-fractions. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].