Graph Linear Functions Using Slope and y-Intercept
Learning Outcome
- Graph a linear function using the slope and y-intercept
[latex]f\left(x\right)=\dfrac{1}{2}x+1[/latex]
The function is in slope-intercept form, so the slope is [latex]\dfrac{1}{2}[/latex]. Because the slope is positive, we know the graph will slant upward from left to right. The y-intercept is the point on the graph when [latex]x=0[/latex]. The graph crosses the y-axis at [latex](0, 1)[/latex]. Now we know the slope and the y-intercept. We can begin graphing by plotting the point [latex](0, 1)[/latex]. We know that the slope is rise over run, [latex]m=\dfrac{\text{rise}}{\text{run}}[/latex]. From our example, we have [latex]m=\dfrac{1}{2}[/latex], which means that the rise is [latex]1[/latex] and the run is [latex]2[/latex]. So starting from our y-intercept [latex](0, 1)[/latex], we can rise [latex]1[/latex] and then run [latex]2[/latex], or run [latex]2[/latex] and then rise [latex]1[/latex]. We repeat until we have a few points and then we draw a line through the points as shown in the graph below.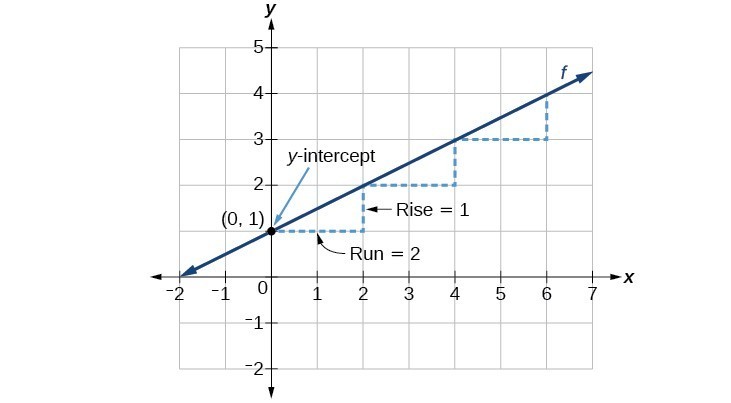
A General Note: Graphical Interpretation of a Linear Function
In the equation [latex]f\left(x\right)=mx+b[/latex]- b is the y-intercept of the graph and indicates the point (0, b) at which the graph crosses the y-axis.
- m is the slope of the line and indicates the vertical displacement (rise) and horizontal displacement (run) between each successive pair of points. Recall the formula for the slope:
[latex]m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{\Delta y}{\Delta x}=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
How To: Given the equation for a linear function, graph the function using the y-intercept and slope
- Evaluate the function at an input value of zero to find the y-intercept.
- Identify the slope.
- Plot the point represented by the y-intercept.
- Use [latex]\dfrac{\text{rise}}{\text{run}}[/latex] to determine at least two more points on the line.
- Sketch the line that passes through the points.
Example
Graph [latex]f\left(x\right)=-\dfrac{2}{3}x+5[/latex] using the y-intercept and slope.Answer:
Evaluate the function at [latex]x=0[/latex] to find the y-intercept. The output value when [latex]x=0[/latex] is [latex]5[/latex], so the graph will cross the y-axis at [latex](0, 5)[/latex].
According to the equation for the function, the slope of the line is [latex]-\dfrac{2}{3}[/latex]. This tells us that for each vertical decrease in the "rise" of [latex]–2[/latex] units, the "run" increases by [latex]3[/latex] units in the horizontal direction. We can now graph the function by first plotting the y-intercept in the graph below. From the initial value [latex](0, 5)[/latex], we move down [latex]2[/latex] units and to the right [latex]3[/latex] units. We can extend the line to the left and right by using this relationship to plot additional points and then drawing a line through the points.
 The graph slants downward from left to right, which means it has a negative slope as expected.
The graph slants downward from left to right, which means it has a negative slope as expected.
Try It
[ohm_question]79774[/ohm_question]Example
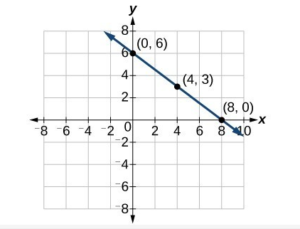
Graph [latex]f\left(x\right)=-\dfrac{3}{4}x+6[/latex] using the slope and y-intercept.Answer:
The slope of this function is [latex]-\dfrac{3}{4}[/latex] and the y-intercept is [latex](0,6)[/latex] We can start graphing by plotting the y-intercept and counting down three units and right [latex]4[/latex] units. The first stop would be [latex](4,3)[/latex], and the next stop would be [latex](8,0)[/latex].
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex: Graph a Line and ID the Slope and Intercepts (Fraction Slope). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- QID 79774: Graph linear eq. in slope-intercept form, give slope and intercept.. Authored by: Day, Alyson. License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
