Multiplying Fractions
Learning Outcomes
- Multiply two or more fractions
- Multiply a fraction by a whole number
Multiply Fractions
Just as you add, subtract, multiply, and divide when working with whole numbers, you also use these operations when working with fractions. There are many times when it is necessary to multiply fractions. A model may help you understand multiplication of fractions. When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have [latex]\dfrac{3}{4}[/latex] of a candy bar and you want to find [latex]\dfrac{1}{2}[/latex] of the [latex]\dfrac{3}{4}[/latex]: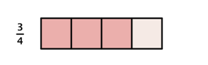 By dividing each fourth in half, you can divide the candy bar into eighths.
By dividing each fourth in half, you can divide the candy bar into eighths.
 Then, choose half of those to get [latex]\dfrac{3}{8}[/latex].
Then, choose half of those to get [latex]\dfrac{3}{8}[/latex].
 In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
Multiplying Two Fractions
[latex-display]\dfrac{a}{b}\cdot\dfrac{c}{d}=\dfrac{a\cdot c}{b\cdot d}=\dfrac{\text{product of the numerators}}{\text{product of the denominators}}[/latex-display]Multiplying More Than Two Fractions
[latex-display]\dfrac{a}{b}\cdot\dfrac{c}{d}\cdot\dfrac{e}{f}=\dfrac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex-display]Example
Multiply [latex]\dfrac{2}{3}\cdot\dfrac{4}{5}[/latex]Answer: Multiply the numerators and multiply the denominators.
[latex]\dfrac{2\cdot 4}{3\cdot 5}[/latex]
Simplify, if possible. This fraction is already in lowest terms.[latex]\dfrac{8}{15}[/latex]
Answer
[latex-display]\dfrac{8}{15}[/latex-display]- Given [latex]\dfrac{8}{15}[/latex], the factors of [latex]8[/latex] are: [latex]1, 2, 4, 8[/latex] and the factors of [latex]15[/latex] are: [latex]1, 3, 5, 15[/latex]. [latex]\dfrac{8}{15}[/latex] is simplified because there are no common factors of [latex]8[/latex] and [latex]15[/latex].
- Given [latex]\dfrac{10}{15}[/latex], the factors of [latex]10[/latex] are: [latex]1, 2, 5, 10[/latex] and the factors of [latex]15[/latex] are: [latex]1, 3, 5, 15[/latex]. [latex]\dfrac{10}{15}[/latex] is not simplified because [latex]5[/latex] is a common factor of [latex]10[/latex] and [latex]15[/latex].
Think About It
Multiply [latex]\dfrac{2}{3}\cdot\dfrac{1}{4}\cdot\dfrac{3}{5}[/latex]. Simplify the answer. What makes this example different than the previous ones? Use the box below to write down a few thoughts about how you would multiply three fractions together. [practice-area rows="2"][/practice-area]Answer: Multiply the numerators and multiply the denominators.
[latex]\dfrac{2\cdot 1\cdot 3}{3\cdot 4\cdot 5}[/latex]
Simplify first by canceling (dividing) the common factors of [latex]3[/latex] and [latex]2[/latex]. [latex]3[/latex] divided by [latex]3[/latex] is [latex]1[/latex], and [latex]2[/latex] divided by [latex]2[/latex] is [latex]1[/latex].[latex]\begin{array}{c}\dfrac{2\cdot 1\cdot3}{3\cdot (2\cdot 2)\cdot 5}\\\dfrac{\cancel{2}\cdot 1\cdot\cancel{3}}{\cancel{3}\cdot (\cancel{2}\cdot 2)\cdot 5}\\\dfrac{1}{10}\end{array}[/latex]
Answer
[latex-display]\dfrac{2}{3}\cdot\dfrac{1}{4}\cdot\dfrac{3}{5}[/latex] = [latex]\dfrac{1}{10}[/latex-display]Licenses & Attributions
CC licensed content, Original
- Adaptation and Revision. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 1: Multiply Fractions (Basic) . Authored by: Mathispower4u. License: CC BY: Attribution.
- Unit 2: Fractions and Mixed Numbers, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
CC licensed content, Specific attribution
- Multiply and Divide Fractions. Provided by: OpenStax Located at: https://openstax.org/books/prealgebra/pages/4-2-multiply-and-divide-fractions. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
