Add and Subtract Radical Expressions
Learning Outcomes
- Determine when two radicals have the same index and radicand
- Recognize when a radical expression can be simplified either before or after addition or subtraction
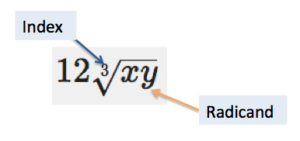 Making sense of a string of radicals may be difficult. One helpful tip is to think of radicals as variables, and treat them the same way. When you add and subtract variables, you look for like terms, which is the same thing you will do when you add and subtract radicals.
In this first example, both radicals have the same radicand and index.
Making sense of a string of radicals may be difficult. One helpful tip is to think of radicals as variables, and treat them the same way. When you add and subtract variables, you look for like terms, which is the same thing you will do when you add and subtract radicals.
In this first example, both radicals have the same radicand and index.
Example
Add. [latex] 3\sqrt{11}+7\sqrt{11}[/latex]Answer: The two radicals are the same, [latex] [/latex]. This means you can combine them as you would combine the terms [latex] 3a+7a[/latex].
[latex] \text{3}\sqrt{11}\text{ + 7}\sqrt{11}[/latex]
The answer is [latex]10\sqrt{11}[/latex].Example
Add. [latex] 5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}[/latex]Answer: Rearrange terms so that like radicals are next to each other. Then add.
[latex] 5\sqrt{2}+2\sqrt{2}+\sqrt{3}+4\sqrt{3}[/latex]
The answer is [latex]7\sqrt{2}+5\sqrt{3}[/latex]Example
Add. [latex] 3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}[/latex]Answer: Rearrange terms so that like radicals are next to each other. Then add.
[latex] 3\sqrt{x}+\sqrt{x}+12\sqrt[3]{xy}[/latex]
The answer is [latex]4\sqrt{x}+12\sqrt[3]{xy}[/latex].Example
Add and simplify. [latex] 2\sqrt[3]{40}+\sqrt[3]{135}[/latex]Answer: Simplify each radical by identifying perfect cubes.
[latex] \begin{array}{r}2\sqrt[3]{8\cdot 5}+\sqrt[3]{27\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}\cdot 5}+\sqrt[3]{{{(3)}^{3}}\cdot 5}\\2\sqrt[3]{{{(2)}^{3}}}\cdot \sqrt[3]{5}+\sqrt[3]{{{(3)}^{3}}}\cdot \sqrt[3]{5}\end{array}[/latex]
Simplify.[latex] 2\cdot 2\cdot \sqrt[3]{5}+3\cdot \sqrt[3]{5}[/latex]
[latex]4\sqrt[3]{5}+3\sqrt[3]{5}[/latex]
The answer is [latex]7\sqrt[3]{5}[/latex].Example
Add and simplify. [latex] x\sqrt[3]{x{{y}^{4}}}+y\sqrt[3]{{{x}^{4}}y}[/latex]Answer: Simplify each radical by identifying perfect cubes.
[latex]\begin{array}{r}x\sqrt[3]{x\cdot {{y}^{3}}\cdot y}+y\sqrt[3]{{{x}^{3}}\cdot x\cdot y}\\x\sqrt[3]{{{y}^{3}}}\cdot \sqrt[3]{xy}+y\sqrt[3]{{{x}^{3}}}\cdot \sqrt[3]{xy}\\xy\cdot \sqrt[3]{xy}+xy\cdot \sqrt[3]{xy}\end{array}[/latex]
Add like radicals.[latex] xy\sqrt[3]{xy}+xy\sqrt[3]{xy}[/latex]
The answer is [latex]2xy\sqrt[3]{xy}[/latex].Subtract Radicals
Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices must be the same for two (or more) radicals to be subtracted. In the three examples that follow, subtraction has been rewritten as addition of the opposite.Example
Subtract. [latex] 5\sqrt{13}-3\sqrt{13}[/latex]Answer: The radicands and indices are the same, so these two radicals can be combined.
[latex] 5\sqrt{13}-3\sqrt{13}[/latex]
The answer is [latex]2\sqrt{13}[/latex].Example
Subtract. [latex] 4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}[/latex]Answer: Two of the radicals have the same index and radicand, so they can be combined. Rewrite the expression so that like radicals are next to each other.
[latex] 4\sqrt[3]{5a}+(-\sqrt[3]{3a})+(-2\sqrt[3]{5a})\\4\sqrt[3]{5a}+(-2\sqrt[3]{5a})+(-\sqrt[3]{3a})[/latex]
Combine. Although the indices of [latex] 2\sqrt[3]{5a}[/latex] and [latex] -\sqrt[3]{3a}[/latex] are the same, the radicands are not—so they cannot be combined.[latex] 2\sqrt[3]{5a}+(-\sqrt[3]{3a})[/latex]
The answer is [latex]2\sqrt[3]{5a}-\sqrt[3]{3a}[/latex].Example
Subtract and simplify. [latex] 5\sqrt[4]{{{a}^{5}}b}-a\sqrt[4]{16ab}[/latex], where [latex]a\ge 0[/latex] and [latex]b\ge 0[/latex]Answer: Simplify each radical by identifying and pulling out powers of [latex]4[/latex].
[latex]\begin{array}{r}5\sqrt[4]{{{a}^{4}}\cdot a\cdot b}-a\sqrt[4]{{{(2)}^{4}}\cdot a\cdot b}\\5\cdot a\sqrt[4]{a\cdot b}-a\cdot 2\sqrt[4]{a\cdot b}\\5a\sqrt[4]{ab}-2a\sqrt[4]{ab}\end{array}[/latex]
The answer is [latex]3a\sqrt[4]{ab}[/latex].Summary
Combining radicals is possible when the index and the radicand of two or more radicals are the same. Radicals with the same index and radicand are known as like radicals. It is often helpful to treat radicals just as you would treat variables: like radicals can be added and subtracted in the same way that like variables can be added and subtracted. Sometimes, you will need to simplify a radical expression before it is possible to add or subtract like terms.Licenses & Attributions
CC licensed content, Original
- Adding Radicals (Basic With No Simplifying). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Adding Radicals That Requires Simplifying. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Subtracting Radicals (Basic With No Simplifying). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Subtracting Radicals That Requires Simplifying. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
